- 计算与表示
计算与表示
“字母表是一项伟大的发明, 使人们能够轻松地储存并学习他人经过艰难努力才获得的知识 —— 也就是说, 可以通过书本学习, 而非通过与真实世界直接且可能痛苦的接触来学习. “
-B.F. Skinner
“这首歌的名字叫作 ‘HADDOCK’S EYES’.” 骑士说道.
“哦, 这就是歌的名字吗? “ 爱丽丝如此问, 努力装作有兴趣.
“不, 你没明白, “ 骑士有些恼火. “这首歌只是名字被 叫作 这个. 这首歌的名字其实是 ‘THE AGED AGED MAN’. “
“那我应该说, ‘这首 歌 被叫做这个’? “ 爱丽丝认真想了想.
“不, 你不该那么说: 那完全是另一回事! 这首 歌 被叫作 ‘WAYS AND MEANS’, 但你知道, 那只是它被 叫作 这个而已! “
“那么, 这首歌究竟 是 什么呢? “ 爱丽丝问道, 此时她已经完全被搞糊涂了.
“我正要说到这点, “ 骑士回答道. “这首歌其实 是 ‘A-SITTING ON A GATE’, 而曲调是我自创的. “
Lewis Carroll, 爱丽丝镜中奇遇
学习目标
- 区分规范与实现, 亦即区分数学函数与算法/程序.
- 将对象表示为字符串(通常由 0 和 1 构成).
- 常见对象(如自然数、向量、列表与图)的表示实例.
- 前缀无关编码.
- Cantor定理: 实数无法被有限长字符串精确表示.
从初步的角度看, 计算 是一个将 输入 映射为 输出 的过程.
在谈论计算时, 一个关键点是要区分两个问题: 需要完成的任务是什么(即规范), 以及 如何去实现这一任务(即实现方式). 例如, 正如我们已经看到的, 计算两个整数的乘积这一任务, 并不只有唯一的一种实现方式.
在本章中, 我们将聚焦于 “是什么” 部分, 即如何定义计算任务. 而这首先要求我们明确定义 输入与输出. 要囊括所有可能的输入和输出似乎颇具挑战性, 因为如今计算已经被应用在各种各样的对象上, 不仅是数字, 还可以是文本, 图像, 视频, 例如社交网络的连接图, MRI 扫描结果, 基因组数据, 甚至是其它程序.
我们将尝试把所有这些对象表示为 由 0 和 1 组成的字符串, 也就是诸如 或任意有限个 与 组成的序列. (当然, 这样的选择只是出于方便, 0 和 1 并非 “神圣” 而不可替代: 我们完全可以用任何其他有限集合的符号来表示.)
如今, 我们已经对数字化的表示习以为常, 因而并不会对这种编码的存在感到惊讶, 但这实际上是一个深刻的结果, 并带来了许多重要的影响. 许多动物也能够表达某种恐惧或欲望, 但人类独特之处在于 语言: 我们使用有限的一组基本符号来描述潜在无限范围的体验. 语言使得信息能够跨越时间与空间进行传递, 并让社会能够涵盖大量的人群, 随时间积累出共享的知识体系.
在过去的几十年里, 我们见证了一场关于数字化表示与传递的革命: 我们现在几乎可以完美地捕捉视觉与听觉的体验, 并几乎瞬间将其传播给无限的受众. 更重要的是, 一旦信息以数字形式存在, 我们便能够对其进行 计算, 并从中获取以往无法触及的数据洞见. 这场革命的核心, 是一个简单却深刻的观察: 我们能够用有限的一组符号 (事实上仅需两个符号 0 和 1) 来表示无穷多样的对象.
在后续的章节中, 我们通常会默认这种表示方法的存在, 因此会使用诸如 “程序 以 为输入” 这样的表述, 即便 可能是一个数字、向量、图, 或者其他任意对象. 不过我们真正的意思是, 的输入实际上是 的 二进制字符串表示. 在本章中, 我们会更深入地探讨如何构造这样的表示方法.
阅读本章, 我们希望读者能够有以下收获:
-
我们可以使用 二进制字符串 来表示所有我们想作为输入和输出的对象. 例如, 可以利用 二进制基 将整数和有理数表示为二进制字符串 (参见 第2.2.1节 和 第2.2节).
-
我们可以通过 组合 简单对象的表示, 来构造复杂对象的表示. 这样一来, 就可以表示整数或有理数的列表, 并进一步用来表示矩阵、图像和图等对象. 前缀无关编码 (prefix-free encoding) 是实现这种组合的一种方式 (参见 第2.5.2节).
-
一个 计算任务 指定了从输入到输出的映射 – 即一个 函数. 区分 “what” 与 “how”, 或者说 规范 (specification) 与 实现 (implementation), 至关重要 (参见 第2.6.1节). 一个函数仅仅定义了哪个输入对应哪个输出, 而并没有规定 如何 从输入计算出输出. 正如我们在乘法的例子中所看到的, 计算同一个函数可能存在多种方式.
-
虽然所有可能的二进制字符串的集合是无限的, 它仍然无法表示 一切. 特别地, 并不存在将 实数 (绝对精确地) 表示为二进制字符串的方法. 这一结果也被称为 Cantor定理 (Cantor’s Theorem) (参见 第2.4节), 通常表述为 “实数是不可数的”. 这也暗示了无限还存在 不同的层次, 不过在本书中我们不会深入讨论这一话题 (参见 备注 2.3).
本章讨论的两个 “核心思想” 是: 重要提示 2.1 – 我们可以通过组合简单对象的表示来表示更复杂的对象; 以及 重要提示 2.2 – 区分 函数 的 “what” 与 程序 的 “how” 至关重要. 后者将是本书中反复提到的一个主题.
2.1 定义表示
每当我们在计算机中存储数字、图像、声音、数据库或其他对象时, 实际上存储在计算机内存中的只是这些对象的 表示.
此外, “表示” 的概念并不限于电子计算机, 当我们写下文字或画一幅图时, 我们同样是在将思想或体验 表示 为符号序列 (这些符号也完全可以是由 0 和 1 构成的字符串), 甚至我们的脑中也并非储存真实的感官输入, 而是仅仅存储它们的 表示.
为了在计算中使用数字、图像、图或其他对象作为输入, 我们需要精确定义如何将这些对象表示为二进制字符串.
一个 表示方案 (representation scheme) 就是将对象 映射到一个二进制字符串 的方法, 例如, 自然数的一个表示方案就是一个函数
当然, 我们不能把所有的数字都表示成相同的字符串 (比如 “”), 一个最基本的要求是, 如果两个数 和 不同, 那么它们必须被表示为不同的字符串, 换句话说, 我们要求编码函数 是 一一对应 的 (one-to-one).
2.1.1 表示自然数
现在我们来展示如何将自然数表示为二进制字符串.
多年来, 人们已经尝试了各种方式来表示数字, 包括绳结计数, 雅玛数字, 罗马数字, 我们熟悉的十进制, 以及许多其它方法. 我们当然可以使用其中任意一种将一个数字表示为字符串 (参见 图 2.3), 然而, 出于计算上的方便, 我们采用 二进制基 作为默认的自然数字符串表示法.
例如, 我们将数字 6 表示为字符串 因为
类似地, 我们将数字 35 表示为字符串 它满足
更多示例见下表.

图 2.3. 将数字 0, 1, 2, …, 9 的每个数字表示为一个 12×8 的位图图像, 该图像可以被视为属于 的一个字符串. 使用这个方案, 我们可以把具有 位十进制数字的自然数 表示为属于 的一个字符串. 图片来源: A. C. Andersen 的博客文章.
| 十进制表示 | 二进制表示 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 5 | 101 |
| 16 | 10000 |
| 40 | 101000 |
| 53 | 110101 |
| 389 | 110000101 |
| 3750 | 111010100110 |
表格: 使用二进制基表示数字. 左列包含自然数在十进制下的表示, 右列包含相同数字在二进制下的表示.
如果 是偶数, 那么 的二进制表示的最低有效位为 如果 是奇数, 那么该位为
就像数字 对应于“去掉“最低有效的十进制位 (例如, 数字 对应于“去掉“最低有效的 二进制 位.
因此, 二进制表示可以形式化定义为以下函数 ( 表示 “natural numbers to strings”):
其中, 是函数, 定义为: 如果 为偶数, 则 如果 为奇数, 则
像往常一样, 对于字符串 表示字符串 与 的连接.
函数 是 递归定义 的: 对于每个 我们通过较小的数字 的表示来定义
同样, 也可以用非递归方式定义 参见 习题 2.2.
在本书的大部分内容中, 将数字表示为二进制字符串的具体选择并不重要: 我们只需要知道这样的表示是存在的.
事实上, 对于许多用途, 我们甚至可以使用更简单的表示方法, 将自然数 映射为长度为 的全零字符串
备注 2.1 (二进制表示的Python实现 (选读)). 我们可以在 Python 中实现如下的二进制表示:
def NtS(n):# 自然数(Natural number) to 字符串(String)
if n > 1:
return NtS(n // 2) + str(n % 2)
else:
return str(n % 2)
print(NtS(236))
# 11101100
print(NtS(19))
# 10011
我们一样可以使用 Python 实现逆向的转换: 将一个字符串映射回它表示的自然数.
def StN(x):# 字符串 to 自然数
k = len(x)-1
return sum(int(x[i])*(2**(k-i)) for i in range(k+1))
print(StN(NtS(236)))
# 236
2.1.2 表示的意义(讨论)
初学时, 我们自然会认为 是“实际“的数字, 而 只是它的表示.
然而, 对于中世纪的大多数欧洲人来说, CCXXXVI 才是“实际“的数字, 而 (如果他们甚至听说过的话)则是奇怪的印度-阿拉伯位置记数法表示. 1
或许未来当我们的 AI 机器人统治者出现时, 它们可能会认为 才是“实际“的数字, 而 只是它们在向人类下达命令时需要使用的表示方法.
那么, 什么才是“实际“的数字呢? 这是数学哲学家们自古以来一直思考的问题.
柏拉图认为, 数学对象存在于某种理想的存在领域中 (在某种程度上比我们通过感官感知的世界更“真实“, 因为后者不过是理想领域的影子).
在柏拉图的视角中, 符号 仅仅是某个理想对象的记号, 为了向 已故音乐家 致敬, 我们可以称之为 “通常由 表示的数字”.
而奥地利哲学家路德维希·维特根斯坦则认为, 数学对象根本不存在, 唯一存在的只有构成 、 或 CCXXXVI 的实际纸上符号.
在维特根斯坦看来, 数学仅仅是对没有固有意义的符号进行形式操作.
你可以将“实际“的数字理解为(有些递归地)“、 和 CCXXXVI 以及所有旨在表示同一对象的过去和未来的表示方式共同指向的那个东西”.
阅读本书时, 你可以自由选择自己的数学哲学, 只要你能区分数学对象本身与表示它们的各种具体方式, 无论是墨迹斑点、屏幕上的像素、零和一, 还是任何其他形式.
2.2 自然数以外对象的表示
我们已经看到, 自然数可以表示为二进制字符串. 而现在我们将展示, 这对于其他类型的对象也同样适用, 包括(可能为负的)整数、有理数、向量、列表、图以及许多其他对象.
在很多情况下, 为一条数据选择“合适的“字符串表示是非常复杂的任务, 寻找“最佳“表示(例如, 最紧凑, 保真度最高, 最易操作、鲁棒性强(抗干扰能力强), 信息量最大等)一直都是研究的热点.
但目前, 我们先专注于展示一些简单的表示方法, 用于将各种对象作为计算的输入和输出.
2.2.1 表示带有负数的全体整数
既然我们可以将自然数表示为字符串, 我们也可以基于此表示 整数 的全集 (即集合 的成员), 只需增加一位用于表示符号.
为了表示一个(可能为负的)数字 我们在自然数 的表示前加上一个比特 若 则 若 则
形式上, 我们将函数 定义如下:
其中, 的定义如 (2.1) 所示.
虽然表示的编码函数必须是一一对应的, 但不必是 满射.
例如, 在上述表示法中, 没有任何数字被表示为空字符串, 但这仍然是有效的表示方法, 因为每个整数都能被唯一地表示为某个字符串.
给定一个字符串 我们如何判断它“应该“表示一个(非负的)自然数还是一个(可能为负的)整数?
更进一步, 即便我们知道 “应该“是一个整数, 我们又如何知道它使用的是哪种表示方案?
事实上, 除非上下文提供该信息, 否则我们不一定知道. (在编程语言中, 编译器或解释器会根据变量的 类型 决定对应变量的比特序列的表示方法.)
我们可以将同一个字符串 视作表示自然数、整数、一段文本、一幅图像, 或者一个绿色的小妖精.
每当我们说类似 “令 为字符串 表示的数字” 这样的句子时, 我们假设固定某种规范表示方案, 比如上文所示的那些.
具体选择哪种表示方案通常无关紧要, 只需要确保在使用时保持一致即可.
2.2.2 补码表示(选读)
第2.2.1节 中使用特定的“符号位“来表示整数的方法被称为 有符号数表示法 (Signed Magnitude Representation), 曾在一些早期计算机中使用.
然而, 二进制补码表示 在实际中更为常见.
整数 在集合 的 二进制补码表示 是长度为 的字符串 定义如下:
其中, 表示数字 的标准二进制表示, 作为长度为 的字符串, 并根据需要用前导零填充.
例如, 如果 则 而
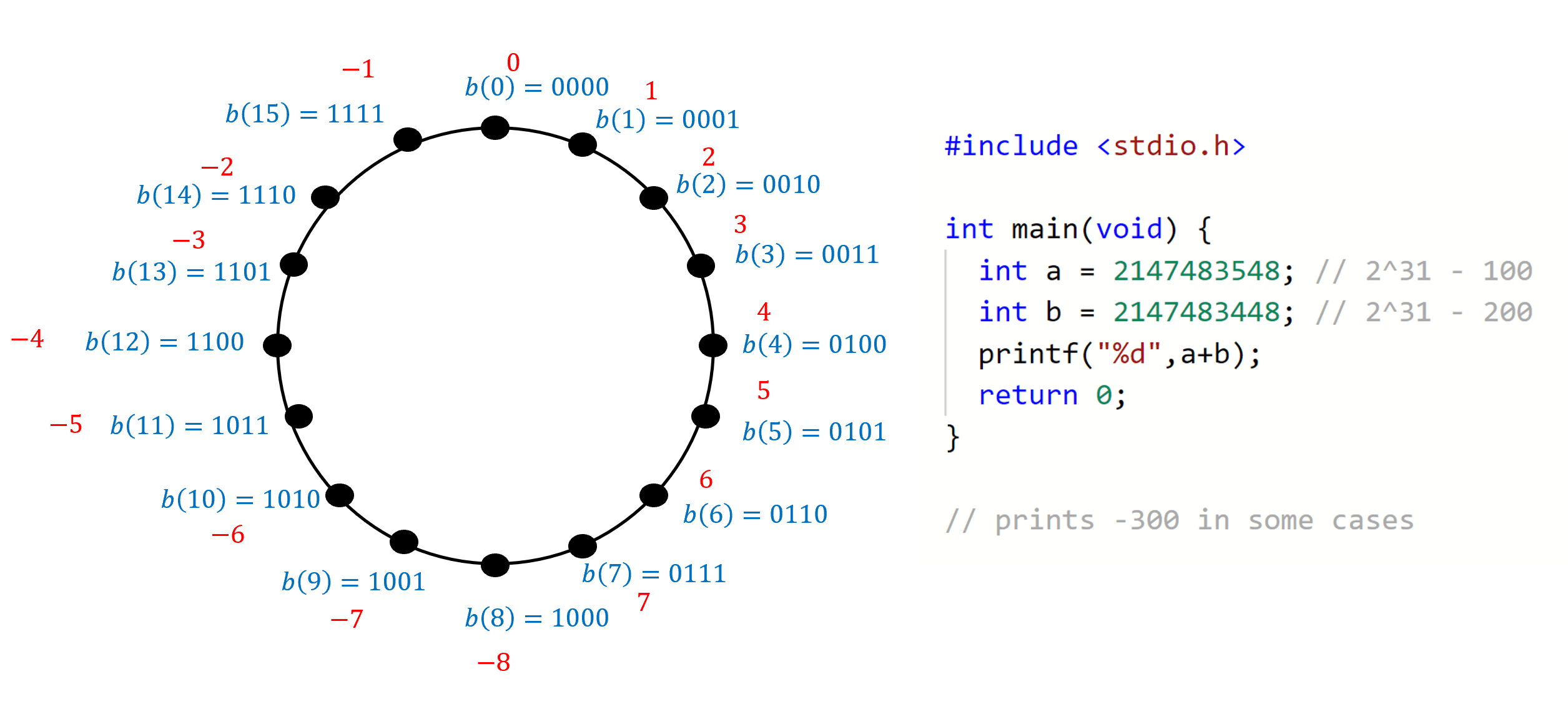
如果 是大于或等于 的负数, 那么 是一个位于 和 之间的数字.
因此, 该数字 的二进制补码表示是长度为 的字符串, 其首位为
换句话说, 我们将一个可能为负的数字 表示为非负数 (参见 图 2.4).
这意味着, 如果两个可能为负的数字 和 不太大 (即 那么我们可以通过将 和 的表示当作非负整数来进行模 加法, 从而得到 的表示.
二进制补码表示的这一特性是其主要优势, 因为根据微处理器的架构, 它们通常可以非常高效地执行模 的算术运算(对于某些 值, 如 32 或 64).
许多系统将检查值是否过大留给程序员, 无论数字大小如何, 系统都会执行这种模运算.
因此, 在某些系统中, 两个大的正数相加可能得到一个 负数 (例如, 将 与 相加可能得到 因为 参见 图 2.4).
2.2.3 有理数及字符串表示对
我们可以通过表示两个数字 和 来表示分数形式的有理数
然而, 仅仅将 和 的表示简单连接起来是行不通的.
例如, 数字 的二进制表示是 数字 的二进制表示是 但将它们简单连接得到的字符串 也可以看作是 的表示 与 的表示 的连接.
因此, 如果使用这种简单连接方式, 我们将无法判断字符串 是表示 还是
我们通过给 字符串对 提供通用表示来解决这个问题.
如果使用纸笔, 我们只需使用一个分隔符号如 将表示数字 和 的一对数字表示为长度为 9 的字符串 “”.
换句话说, 存在一个一一对应的映射 将 字符串对 映射为一个在字母表 上的单个字符串 (即
使用分隔符类似于英语中使用空格和标点来分隔单词.
通过增加少量冗余, 我们可以在数字领域实现同样的效果.
我们可以将三元素集合 映射到三元素集合 并保持一一对应, 从而将长度为 的字符串 编码为长度为 的字符串
我们对有理数的最终表示通过以下步骤组合得到:
- 将一个(可能为负的)有理数表示为一对整数 使得
- 将整数表示为二进制字符串.
- 将步骤 1 和 2 结合, 得到有理数作为字符串对的表示.
- 将 上的字符串对表示为 上的单个字符串.
- 将 上的字符串表示为更长的 字符串.
同样的思想可以用来表示字符串三元组、四元组, 甚至更多, 作为单个字符串.
实际上, 这是一个非常通用的原则的实例, 我们会在计算机科学的理论与实践中反复使用它(例如, 在面向对象编程中):
重复同样的思想, 一旦我们可以表示类型为 的对象, 我们也可以表示这些对象的 列表的列表, 甚至是列表的列表的列表, 如此类推.
当我们讨论 第2.5.2节 中的 前缀无关编码 (prefix free encoding) 时, 我们会再次回到这一点.
2.3 实数的表示
实数集 包含所有正数、负数、分数, 以及像 或 这样的 无理数.
每个实数都可以用有理数近似, 因此我们可以用一个接近 的有理数 来表示实数
例如, 我们可以用 来表示 误差约为 若希望误差更小(例如约 可以使用 以此类推.
实数通过近似有理数来表示是一个可行的表示方案.
然而, 在计算机应用中, 通常更常用 浮点表示法 (参见 图 2.5) 来表示实数.
在浮点表示法中, 我们用一对 表示 其中 和 是某些规定长度的(可能为正或负的)整数, 并且 最接近
浮点表示是 科学计数法 的二进制版本, 即将一个数字 表示为 的近似.
称之为“浮点“是因为可以将 看作指定一串二进制数字, 描述这串数字中“二进制小数点“的位置.
正是浮点表示的使用, 导致许多编程系统中, 表达式 0.1+0.2 的输出为 0.30000000000000004 而不是 0.3.
更多信息可见: 这里, 这里, 这里.
读者可能会(合理地)担心, 浮点表示法(或有理数表示法)只能 近似 表示实数.
在许多(但不是全部)计算应用中, 可以将精度调得足够高, 以至于不会影响最终结果.
但有时我们仍需要谨慎. 事实上, 浮点数错误有时可能造成严重后果.
例如, 浮点舍入误差曾导致美国爱国者导弹未能拦截伊拉克飞毛腿导弹, 造成 28 人死亡 (详细报道), 以及在计算 英国养老金发放金额 时出现过的 1 亿英镑的错误.
2.4 Cantor定理, 可数集, 以及实数的字符串表示
“对于任意一组水果, 我们可以制作的水果沙拉数量总可以比水果数量更多. 如果不是这样, 我们可以给每个沙拉贴上一个不同水果的标签, 最后再考虑这样一个沙拉, 它包含所有未被标签所指的水果, 那么某个水果恰好在这个沙拉的标签中当且仅当它不在其中.”
鉴于浮点数对实数的近似问题, 一个自然的问题是: 是否可以将实数 精确地 表示为字符串.
不幸的是, 下述定理表明这是不可能的:
不存在一一对应的函数 2
可数集. 我们说一个集合 是 可数的, 如果存在一个满射 或者换句话说, 我们可以将 写成序列
由于二进制表示给出了从 到 的满射, 并且两个满射的复合仍然是满射, 集合 是可数的当且仅当存在从 到 的满射.
利用函数的基本性质(见 第1.4.3节), 一个集合可数当且仅当存在从 到 的一一函数.
因此, 我们可以将 定理 2.1 重述如下:
定理 2.2 由 Georg Cantor 于 1874 年证明.
这一结果(以及相关结论)震惊了当时的数学家. 通过证明不存在从 到 (或 的一一映射, Cantor 展示了这两个无限集合有“不同的无限形式“, 并且实数集 在某种意义上比无限集合 “更大”.
“无限的层次“这一概念当时让数学家和哲学家深感困惑. 哲学家 Ludwig Wittgenstein(前面提到过)称 Cantor 的结果为“完全的胡扯“且“可笑”, 其他人甚至认为更糟: Leopold Kronecker 称 Cantor 是“腐蚀青年的人“, 而 Henri Poincaré 说 Cantor 的思想“应从数学中彻底剔除“.
不过事实证明 Cantor 看得更远. 如今 Cantor 的工作已被普遍接受为集合论和数学基础的基石.
正如 David Hilbert 在 1925 年所说, “无人能将我们从 Cantor 为我们创造的天堂中驱逐出去”.
也正如我们稍后将在本书中看到的, Cantor 的思想在计算理论中也起着重要作用.
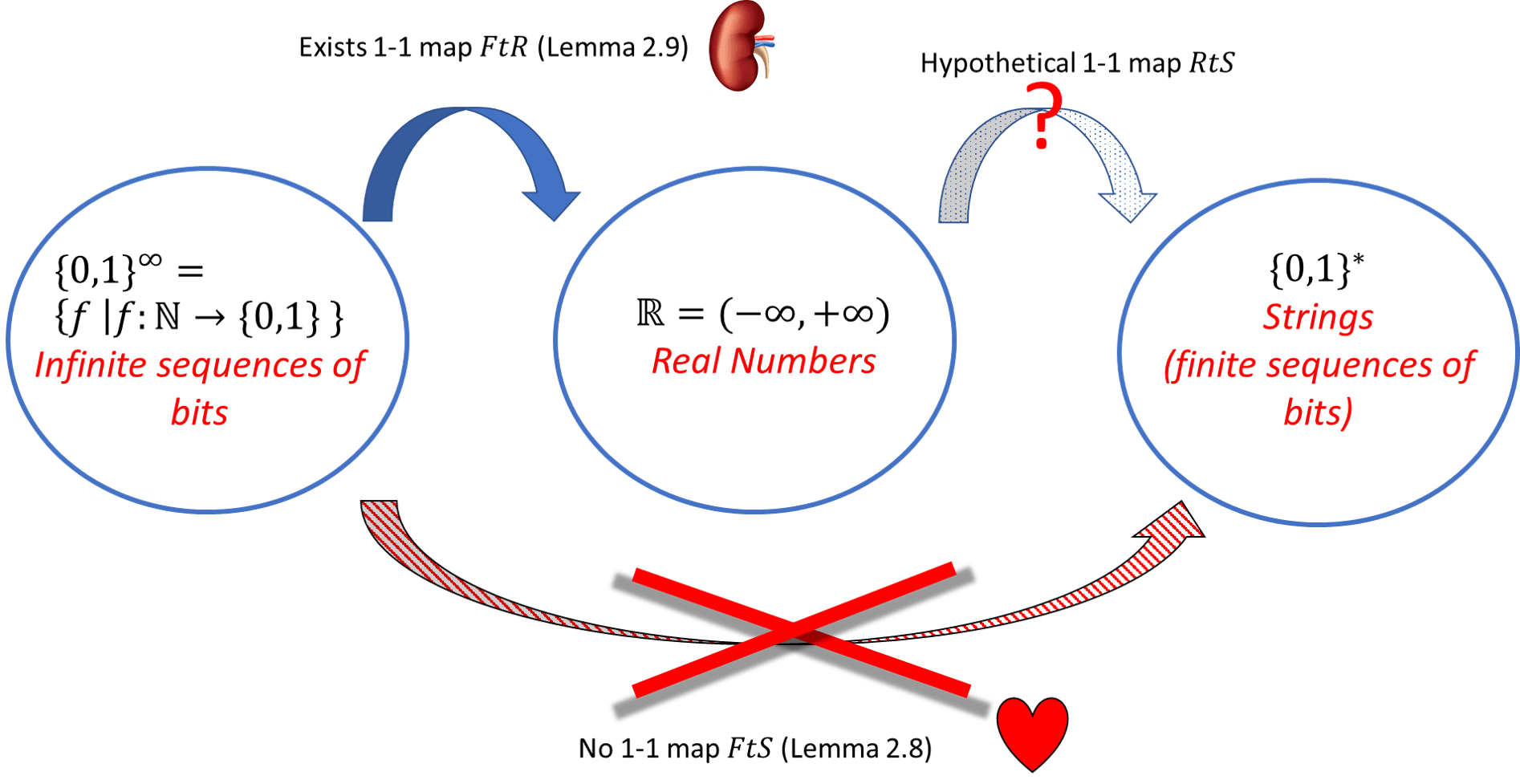
我们已经讨论了 定理 2.1 的重要性, 让我们来看看它的证明. 这将分两步进行:
- 定义一个无限集合 对于它证明不可数更加容易(即证明不存在从 到 的一一函数更容易).
- 证明存在一个一一函数 将 映射到
利用反证法, 这两条事实结合起来可以推出 定理 2.1.
具体来说, 如果假设(为了反证)存在某个一一函数 将 映射到
那么通过将 与步骤 2 中的函数 复合得到的函数 就是从 到 的一一函数,
这与步骤 1 中的结论矛盾!
为了将这个想法完整地转化为 定理 2.1 的证明, 我们需要:
- 定义集合
- 证明不存在从 到 的一一函数.
- 证明存在从 到 的一一函数.
接下来我们将精确地做到这些:
我们将定义集合 它将扮演 的角色,
然后陈述并证明两个引理, 说明该集合满足我们所需的两个性质.
简单来说, 是一个 函数的集合, 并且一个函数 属于 当且仅当它的定义域是 而值域是
我们可以将 理解为所有无限长 比特序列 的集合, 因为函数 正好一一对应于无限序列
下面两个引理说明, 可以作为 来证明 定理 2.1:
引理 2.1. 不存在从 到 的一一映射 3
引理 2.2. 存在从 到 的一一映射 4
如上所示, 引理 2.1 和 引理 2.2 结合起来即可推出 定理 2.1.
为了更正式地重复这一论证, 为了反证, 假设存在一一函数
由 引理 2.2, 存在一一函数
因此, 根据假设, 由于两个一一函数的复合仍是一一函数(见 习题 2.12),
函数 定义为 将是一一函数,
这与 引理 2.1 矛盾.
参见 图 2.7 获取该论证的图示说明.
现在只剩下证明这两个引理. 我们先从证明 引理 2.1 开始, 这实际上是 定理 2.1 的核心部分.
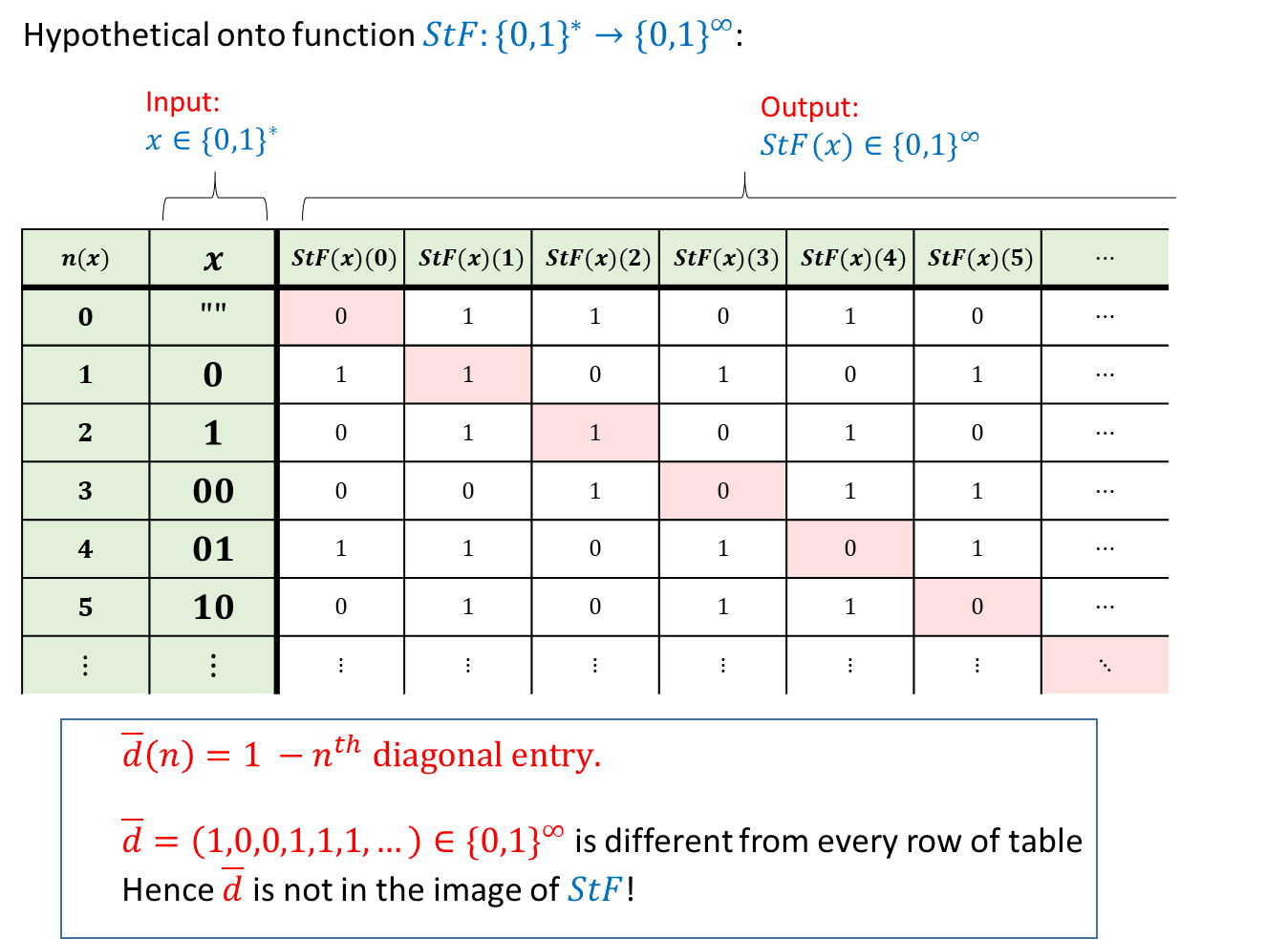
热身运动: “Cantor定理青春版”. 引理 2.1 的证明相当微妙. 一种获得对该证明的直觉的方法是考虑以下有限版本的陈述: “不存在一个满射函数 ”. 当然我们知道这是正确的, 因为集合 比集合 更大, 但让我们来看一个不太直接的证明: 对于任意 我们可以定义字符串 如下: 如果 是满射, 那么必然存在某个 使得 但我们声称不存在这样的 实际上, 如果存在这样的 那么 的第 个分量应当等于 但根据定义这个分量等于 另见此陈述的 “proof by code”.
对引理 2.1的证明
对引理 2.1的证明
我们将证明不存在一个 满射 函数
这将推出该引理, 因为对于任意两个集合 和 当且仅当存在一个从 到 的一一映射时, 才存在一个从 到 的满射 (见 引理 1.1).
这个证明技巧被称为 “diagonal argument” (对角线论证), 详情可见 图 2.8.
为了得到矛盾, 我们假设存在这样一个函数 然后我们通过构造一个函数 使得对每个 都有 来证明 不是满射.
考虑二进制字符串的字典序排列 (即 “”,
对于每个 我们令 为此顺序中的第 个字符串.
也就是说 等等.
对每个 我们定义函数 如下:
也就是说, 为了计算 在输入 时的值, 我们首先计算 其中 是字典序中的第 个字符串.
由于 它是一个将 映射到 的函数.
值 被定义为 的取反.
函数 的定义有些微妙.
一种理解方式是将函数 想象为由一张无限长的表格指定, 其中每一行对应一个字符串 (字符串按字典序排列), 并包含序列
然后, 我们取该表格中的 对角线 元素如下:
这些元素对应于表格中第 行第 列的 对于
我们上面定义的函数 将每个 映射到第 个对角线元素的取反值.
为了完成 不是满射的证明, 我们需要说明对每个 都有
事实上, 令 为某个字符串, 并令
如果 是 在字典序中的位置, 则根据构造有 这意味着 这正是我们需要的.
引理 2.1 实际上与自然数或字符串没有太大关系.
仔细审视这个证明可以发现, 它实际上说明对于 任意 集合 不存在一个一一映射 其中 表示所有以 为定义域的布尔函数的集合
由于我们可以将子集 与其特征函数 对应 (即 当且仅当 我们也可以将 看作 的所有 子集 的集合.
这个子集集合有时被称为 的 幂集, 记作 或
引理 2.1 的证明可以推广, 说明不存在一个集合与其幂集之间的一一映射.
特别地, 这意味着集合 “比” 更大.
Cantor 利用这些思想构建了无限的无穷层级.
这些无穷的数量远大于 甚至
他将 的基数记作 并将下一个更大的无限数记作 ( 是希伯来字母表的第一个字母).
Cantor 还提出了 连续统假设, 即
我们将在本书后续回到这个假设背后的精彩故事.
Aaronson 的这节讲座 提到了一些相关问题 (另见 Berkeley CS 70 lecture).
为了完成 定理 2.1 的证明, 我们需要证明 引理 2.2.
这个证明虽然需要一些微积分基础, 但使用了的地方都比较直接易懂.
不过如果你之前处理实数列极限的经验不多, 那么下面的证明还是可能会有些难以理解.
当然, 这部分并非 Cantor 论证的核心, 此类极限对于本书后续内容也不重要, 因此你完全可以选择相信 引理 2.2 并跳过这些繁琐的证明.
对引理 2.2的证明思路
对引理 2.2的证明思路
我们定义 为介于 和 之间的数, 其十进制展开为 换句话说,
如果 和 是 中的两个不同函数, 那么必然存在某个输入 使它们在该输入上不一致.
取最小的这样的 那么数字 与 在小数点后的第 到 位完全相同, 并在第 位上不同.
因此这些数字必然不同.
具体来说, 如果 且 则第一个数字大于第二个; 否则 ( 且 第一个数字小于第二个.
在证明中我们需要稍微注意, 因为某些数字可以被 无限展开, 例如, 数字 有两种十进制展开: 和
但在这里不会出现这个问题, 因为按上述定义, 我们使用的数字的十进制展开中永远不会包含数字
对引理 2.2的证明
对引理 2.2的证明
对于每个 我们定义 为其十进制展开为 的数字.
形式上,
在微积分中有一个已知结论(这里我们不重复证明): (2.2) 右侧的级数在 中收敛到一个确定的极限.
现在我们证明 是一一映射.
设 是 中的两个不同函数.
由于 和 不同, 必然存在某个输入它们的值不同, 我们令 为最小的这样的输入, 并且不失一般性地假设 且
(否则, 如果 且 我们可以简单地交换 和 的角色.)
数字 和 在小数点后的前 位完全相同.
由于这第 位在 中为 而在 中为 我们声称 比 至少大
要理解这一点, 注意 的差值在以下情况下最小: 对于所有 且 此时(由于 和 在前 位相同)
由于无穷级数 收敛到 可得对于每一对这样的 和
特别地, 我们看到对于每一对不同的 从而函数 是一一映射.
在上面的证明中, 我们使用了级数 收敛到 的事实, 将其代入 (2.3) 可得 与 的差值至少为
虽然我们为 选择的十进制表示是任意的, 但我们不能用二进制表示代替.
如果使用 二进制 展开而非十进制, 相应的级数 收敛到 并且由于 我们无法推导出 是一一映射.
事实上, 确实存在一些不同的序列对 满足
(例如, 序列 与序列 就具有此性质.)
2.4.1 推论: 布尔函数全体不可数.
Cantor 定理得出如下推论, 我们将在本书中多次使用: 所有 布尔函数(将 映射到 的函数)构成的集合是不可数的.
这是 引理 2.1 的直接推论, 因为我们可以用二进制表示构造一个从 到 的一一映射. 因此, 的不可数性意味着 的不可数性.
对定理 2.3的证明
对定理 2.3的证明
由于 是不可数的, 我们只需展示一个从 到 的一一映射, 便可得到该结论.
原因在于, 这样的映射存在意味着如果 是可数的, 从而存在一个从 到 的一一映射, 那么就会存在一个从 到 的一一映射, 与 引理 2.1 矛盾.
现在我们展示这个一一映射. 我们简单地将一个函数 映射到函数 如下.
我们令 等等.
也就是说, 对于每个 如果它在二进制下表示自然数 我们定义
如果 不表示这样的数字(例如, 它有前导零), 则我们令
这个映射是一一映射, 因为如果 是 中的两个不同元素, 那么必然存在某个输入 使
于是, 如果 是表示 的字符串, 我们看到 其中 是 映射到的 中的函数, 而 是 映射到的函数.
2.4.2 可数性的等价条件
上述结果建立了多种等价的方式来表述集合可数的事实.
具体来说, 以下陈述都是等价的:
- 集合 是可数的
- 存在一个从 到 的满射
- 存在一个从 到 的满射
- 存在一个从 到 的一一映射
- 存在一个从 到 的一一映射
- 存在一个从某个可数集合 到 的满射
- 存在一个从 到某个可数集合 的一一映射
2.5 数字以外元素的表示
当然, 数字并不是我们唯一可以表示为二进制字符串的对象.
用于表示某个集合 中对象的 表示方案 由一个将 中对象映射为字符串的 编码 函数和一个将字符串解码回 中对象的 解码 函数组成.
形式化地, 我们作如下定义:
注意, 对每个 都有 的条件意味着 是 满射(你能看出为什么吗? ).
事实上, 构造一个表示方案时, 我们只需要找到一个 编码 函数.
也就是说, 每个一一的编码函数都有对应的解码函数, 如下引理所示:
对引理 2.3的证明
对引理 2.3的证明
设 为 中任意一个元素.
对于每个 要么不存在, 要么仅存在一个 使 (否则 将不是一一映射).
我们将 定义为在第一种情况取 在第二种情况取该唯一对象
根据定义, 对每个 都有
虽然表示方案的解码函数通常可以是一个 局部 函数, 但 引理 2.3 的证明表明, 每个表示方案都有一个 全域 解码函数. 这一观察有时是很有用的.
2.5.1 有限表示
如果 是 有限 的, 那么我们可以将 中的每个对象表示为长度至多为某个数 的字符串.
那么 的取值是多少呢?
我们记 为长度至多为 的字符串集合
集合 的大小等于
这使用 等比数列 的标准求和公式即可得到.
为了将 中的对象表示为长度至多为 的字符串, 我们需要构造一个从 到 的一一映射. 而当且仅当 我们才能做到这一点, 如以下引理所示:
对于任意两个非空有限集合 当且仅当 时, 存在一个一一映射
设 且 并将 和 的元素分别写为 和
我们需要证明, 存在一个一一映射 当且仅当
对“当“方向, 如果 我们可以简单地定义 对每个
显然, 对于 有 因此该函数是一一映射.
对“仅当“方向, 假设 且 是某个函数. 那么 不可能是一一映射.
事实上, 对 我们“标记“ 中的元素
如果 已经被标记过, 那么我们就找到了两个映射到同一元素 的 中的对象.
否则, 由于 有 个元素, 当我们标记到 时, 中的所有对象都已被标记.
因此, 在这种情况下, 必须映射到一个已经被标记过的元素.
(这一观察有时被称为“鸽巢原理“: 假设有 个巢和 只鸽子, 则必有两只鸽子在同一个巢中.)
2.5.2 前缀无关编码
在展示有理数的表示方案时, 我们使用了一个“技巧“: 将字母表 编码, 以便将字符串元组表示为单个字符串.
这是 前缀无关编码 的一个特例.
前缀无关编码的思想如下, 如果我们的表示具有如下性质: 表示对象 的字符串 不是表示不同对象 的字符串 的 前缀 (即初始子串), 那么我们可以仅通过将列表中所有成员的表示串联起来, 来表示一个对象列表.
例如, 因为在英文中每个句子都以标点符号结束, 如句号, 感叹号或问号, 没有句子可以成为另一个句子的前缀, 因此我们可以仅通过将句子一个接一个地串联来表示一个句子列表. (英文中存在一些复杂情况, 例如缩写中的句点 (如 “e.g.”)或句子引号包含标点, 但高层次上前缀自由表示句子的原理仍然成立.)
事实上, 我们可以将 每一个 表示转换为前缀无关形式.
这为 重要提示 2.1 提供了依据, 并允许我们将类型 对象的表示方案转换为类型 对象 列表 的表示方案.
通过重复同样的技术, 我们还可以表示类型 对象的列表的列表, 以此类推.
但首先, 让我们正式定义前缀无关性:
回忆一下, 对于每个集合 集合 包含所有有限长度的元组(即 列表)的 中元素.
下述定理表明, 如果 是 的前缀自由编码, 则通过串联编码, 我们可以得到 的一个有效的(一一)表示:
定理 2.4 可能有点难以理解, 但一旦你理解了它的含义, 实际上证明起来相当直接.
因此, 我强烈建议你在此处停下来, 确保你理解了该定理的陈述. 你也应该尝试自己证明它, 然后再继续阅读.
证明的思路很简单.
例如, 假设我们想从表示 中解码三元组
我们首先找到 的第一个前缀 它是某个对象的表示.
然后解码该对象, 从 中去掉 得到新的字符串 再继续找到 的第一个前缀 以此类推(参见 习题 2.9).
的前缀自由性质保证了 实际上就是 是 依此类推.
对定理 2.4的证明
对定理 2.4的证明
现在我们给出正式证明.
使用反证法, 假设存在两个不同的元组 和 使得
我们将字符串 记为
设 为第一个使得 的索引.
(如果对所有 都有 由于假设这两个元组不同, 则其中一个元组的长度必须大于另一个. 在这种情况下, 不失一般性, 我们假设 并令 )
在 的情况下, 我们看到字符串 可以用两种不同的方式表示:
以及
其中 对所有 成立.
令 为从 中去掉前缀 后得到的字符串.
我们看到 可以写成两种形式: 对某个字符串 也可以写成 对某个
但这意味着 与 中的一个必须是另一个的前缀, 这与 的前缀自由性矛盾.
若 且 我们通过如下方式得到矛盾: 在这种情况下
这意味着 必须对应于空字符串
但在这种情况下, 也必须是空字符串, 而空字符串显然是任意其他字符串的前缀, 这与 的前缀自由性矛盾.
备注 2.6 (列表表示的前缀无关性).
即使集合 中对象的表示 是前缀无关的, 也并不意味着这些对象的 列表 的表示 也会是前缀无关的. 例如: 对于任意三个对象 列表 的表示将是列表 的表示的前缀.
然而, 如下的 引理 2.4 所示, 我们可以将 每一个 表示转换为前缀无关的, 因此如果需要表示列表的列表、列表的列表的列表等, 我们就可以使用该转换.
2.5.3 构造前缀无关表示
有一些自然的表示是前缀无关的.
例如, 每个 固定输出长度 的表示(即一一函数 自动是前缀无关的, 因为只有当 和 相等时, 长度相同的 才可能有 作为前缀.
此外, 我们用来表示有理数的方法也可以用来证明如下结论:
为了完整起见, 我们将在下方给出证明. 不过你可以在这里停下来, 尝试用我们表示有理数时使用的相同技巧自己证明它.
对引理 2.4证明
对引理 2.4证明
证明的核心思想是使用映射 来“加倍“字符串 中的每一位, 然后通过在其后拼接 来标记字符串的结束.
如果我们以这种方式对字符串 进行编码, 它可以确保 的编码绝不会是不同字符串 的编码的前缀.
形式上, 我们对每个 定义函数 如下:
如果 是 的(可能不是前缀无关的)表示, 我们可以通过定义 将其转换为前缀无关的表示
为了证明该引理, 我们需要证明 (1) 是一一函数, 并且 (2) 是前缀无关的.
事实上, 前缀无关是比一一更强的条件(如果两个字符串相等, 则其中一个必然是另一个的前缀), 因此只需证明 (2) 即可, 我们现在来证明它.
设 为 中两个不同的对象.
我们将证明 不是 的前缀, 或换句话说, 不是 的前缀, 其中
由于 是一一函数, 所以 我们分三种情况讨论, 取决于 或
- 如果 则 中位置 的两位为 而 中对应位将等于 或 (取决于 的第 位), 因此 不可能是 的前缀.
- 如果 由于 必然存在某个位置 使它们不同, 这意味着 和 在位置 上不同, 同样 不是 的前缀.
- 如果 则 因此 比 长, 不可能是其前缀.
在所有情况下, 我们可以预见 都不是 的前缀, 从而完成了证明.
引理 2.4 的证明并不是将任意表示转换为前缀无关形式的唯一方法, 也不一定是最优方法.
习题 2.10 就要求你构造一个更高效的前缀无关转换, 满足
2.5.4 “基于Python的证明” (选读)
定理 2.4 和 引理 2.4 的证明是 构造性的, 意味着它们给出了:
- 将任意对象 的表示的编码和解码函数转换为前缀无关的编码和解码函数的方法, 以及
- 将单个对象的前缀无关编码和解码扩展到 对象列表 的编码和解码的方法(通过串联实现).
具体来说, 我们可以将任意一对 Python 函数 encode 和 decode 转换为函数 pfencode 和 pfdecode, 对应于前缀无关的编码和解码.
同样, 给定单个对象的 pfencode 和 pfdecode, 我们可以将它们扩展到列表的编码.
下面展示了如何对上文定义的 NtS 和 StN 函数进行这种处理.
我们从 引理 2.4 的“Python 证明“开始: 一种将任意表示转换为 前缀无关 表示的方法.
下面的函数 prefixfree 接受一对编码和解码函数作为输入, 并返回一个三元组函数, 其中包含 前缀无关 的编码和解码函数, 以及一个检查字符串是否为对象有效编码的函数.
# 接受 encode 和 decode 函数, 分别将对象映射为比特列表以及反向映射,
# 并返回 pfencode 和 pfdecode 函数,
# 以前缀无关的方式将对象映射为比特列表以及反向映射.
# 同时返回一个 pfvalid 函数, 用于判断一个比特列表是否为有效编码
def prefixfree(encode, decode):
def pfencode(o):
L = encode(o)
return [L[i//2] for i in range(2*len(L))]+[0,1]
def pfdecode(L):
return decode([L[j] for j in range(0,len(L)-2,2)])
def pfvalid(L):
return (len(L) % 2 == 0 ) and all(L[2*i]==L[2*i+1] for i in range((len(L)-2)//2)) and L[-2:]==[0,1]
return pfencode, pfdecode, pfvalid
pfNtS, pfStN , pfvalidN = prefixfree(NtS,StN)
NtS(234)
# 11101010
pfNtS(234)
# 111111001100110001
pfStN(pfNtS(234))
# 234
pfvalidM(pfNtS(234))
# true
注意, 上述 Python 函数 prefixfree 接受两个 Python 函数 作为输入, 并输出三个 Python 函数作为结果. (无歧义的情况下, 我们会使用 “Python 函数” 或 “子程序” 这个术语来区分 Python 程序片段和数学意义上的函数.)
在本书中, 你不需要掌握 Python, 但你需要熟悉函数作为独立的数学对象的概念, 可以被用作其他函数的输入或输出.
下面我们给出 定理 2.4 的 “Python 证明”. 具体来说, 我们展示一个函数 represlists, 它接受一个前缀无关表示方案作为输入 (通过编码、解码和有效性检测函数实现), 并输出一个用于表示该类对象 列表 的表示方案. 如果我们希望使这个表示也是前缀无关的, 那么可以再将其放入上面的 prefixfree 函数中.
def represlists(pfencode,pfdecode,pfvalid):
"""
接受函数 pfencode, pfdecode 和 pfvalid,
并返回函数 encodelists, decodelists,
它们可以分别对该类对象的 **列表** 进行编码和解码.
"""
def encodelist(L):
"""Gets list of objects, encodes it as list of bits"""
return "".join([pfencode(obj) for obj in L])
def decodelist(S):
"""Gets lists of bits, returns lists of objects"""
i=0; j=1 ; res = []
while j<=len(S):
if pfvalid(S[i:j]):
res += [pfdecode(S[i:j])]
i=j
j+= 1
return res
return encodelist,decodelist
LtS , StL = represlists(pfNtS,pfStN,pfvalidN)
LtS([234,12,5])
# 111111001100110001111100000111001101
StL(LtS([234,12,5]))
# [234, 12, 5]
2.5.5 字母和文本的表示
我们可以用一个字符串来表示一个字母或符号, 然后如果这种表示是前缀无关的, 我们就可以通过简单地连接每个符号的表示来表示一个符号序列.
其中一种表示是 ASCII, 它用 7 位的字符串表示 128 个字母和符号.
由于 ASCII 表示是固定长度的, 它自动是前缀无关的 (你能看出原因吗?).
Unicode 是一种将 (在撰写本文时) 约 128,000 个符号表示为介于 0 和 1,114,111 之间的数字的表示方法 (称为 code points).
对于这些 code points 有几种前缀无关的表示方法, 一种流行的方法是 UTF-8, 它将每个 code point 编码为长度在 8 到 32 之间的字符串.
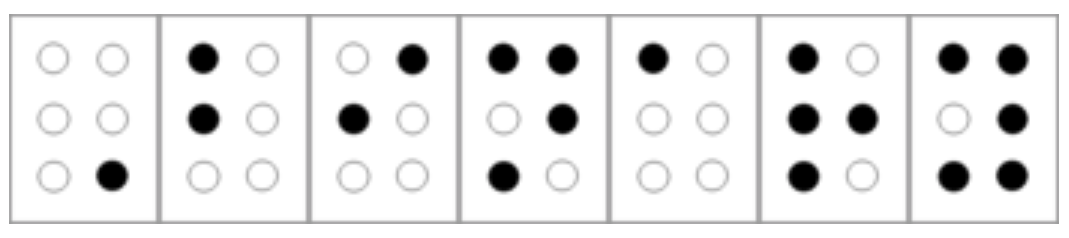
样例 2.2 (Braille 编码(盲文)).
Braille 编码(盲文) 是另一种将字母和其他符号编码为二进制字符串的方法. 具体来说, 在盲文中, 每个字母被编码为一个属于 的字符串, 该字符串通过排列成两列三行的凸起点来书写, 参见 图 2.10.
(一些符号需要用超过一个六位字符串来编码, 因此盲文使用了更通用的前缀无关编码.)
Louis Braille 是一个法国男孩, 因事故在 5 岁时失明. 盲文由 Braille 于 1821 年发明, 当时他只有 12 岁 (尽管他在一生中不断改进和完善它).
样例 2.3 (C语言中对象的表示(选读)).
我们可以使用编程语言来探究我们的计算环境如何表示各种数值.
在允许直接访问内存的 “不安全” 编程语言(如 C语言)中, 这种操作最为简单.
使用一个 简单的 C 程序, 我们可以得到各种数值的表示方法.
可以看到, 对于整数, 乘以 2 对应于每个字节内部的 “左移”.
相比之下, 对于浮点数, 乘以 2 对应于表示中指数部分加 1.
在我们使用的架构中, 负数使用 二进制补码 方法表示.
C语言通过确保字符串末尾有一个零字节, 来以前缀无关的形式表示字符串.
int 2 : 00000010 00000000 00000000 00000000
int 4 : 00000100 00000000 00000000 00000000
int 513 : 00000001 00000010 00000000 00000000
long 513 : 00000001 00000010 00000000 00000000 00000000 00000000 00000000 00000000
int -1 : 11111111 11111111 11111111 11111111
int -2 : 11111110 11111111 11111111 11111111
string Hello: 01001000 01100101 01101100 01101100 01101111 00000000
string abcd : 01100001 01100010 01100011 01100100 00000000
float 33.0 : 00000000 00000000 00000100 01000010
float 66.0 : 00000000 00000000 10000100 01000010
float 132.0: 00000000 00000000 00000100 01000011
double 132.0: 00000000 00000000 00000000 00000000 00000000 10000000 01100000 01000000
2.5.6 向量, 矩阵及图片的表示
一旦我们可以表示数字和数字列表, 我们就可以表示 向量(本质上就是数字的列表).
同样, 我们可以表示列表的列表, 因此特别地, 可以表示 矩阵.
为了表示一张图像, 我们可以通过一个长度为3的数字列表表示每个像素的颜色, 分别对应红色、绿色和蓝色的强度.
(我们可以只使用三种原色, 因为 大多数 人类视网膜中只有三种类型的视锥细胞; 而如果要表示 螳螂虾 可见的颜色, 我们需要 16 种原色.)
因此, 一张包含 个像素的图像可以表示为一个包含 个长度为三的列表的列表.
视频可以表示为图像的列表.
当然, 这些表示方法相当浪费, 对于图像和视频通常使用 更 紧凑 的表示方法, 虽然本书不会涉及这些内容.
2.5.7 图的表示
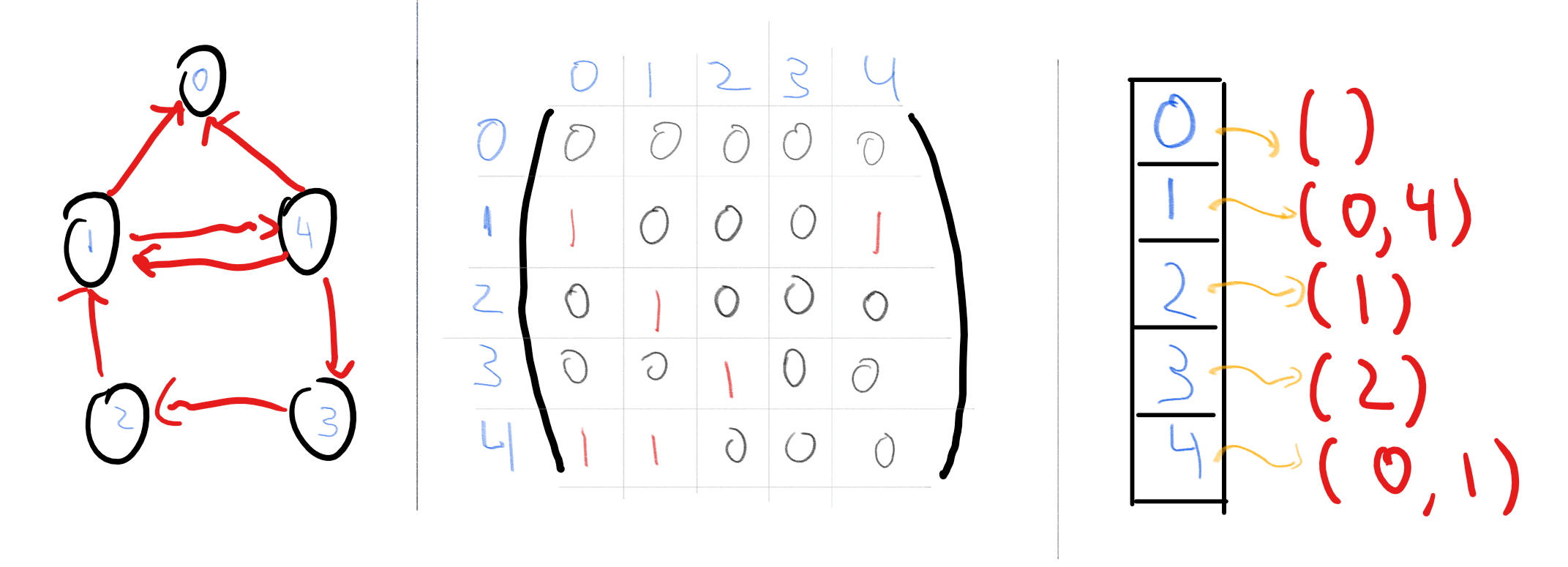
一个 图 在 个顶点上可以表示为一个 的 邻接矩阵, 其第 个元素为 1 当且仅当边 存在, 否则为 0.
也就是说, 我们可以将一个 顶点的有向图 表示为一个字符串 使得 当且仅当边
我们可以通过将每条无向边 替换为两条有向边 和 来将无向图转换为有向图.
另一种图的表示方法是 邻接表 表示. 也就是说, 我们将图的顶点集合 与集合 对应, 其中 并将图 表示为 个列表组成的列表, 其中第 个列表包含顶点 的出邻居.
对于某些应用, 这些表示方法之间的差异可能很大, 虽然对于我们而言通常无关紧要.
2.5.8 列表和嵌套列表的表示
如果我们有一种方法将集合 中的对象表示为二进制字符串, 那么我们可以通过应用前缀无关变换来表示这些对象的列表.
此外, 我们可以使用类似上述的技巧来处理 嵌套 列表.
其思想是, 如果我们有某种表示 那么我们可以使用五元素字母表 0,1,[ , ] , , 上的字符串来表示来自 的嵌套列表.
例如, 如果 表示为 0011, 表示为 10011, 表示为 00111, 那么我们可以将嵌套列表 表示为字母表 上的字符串 "[0011,[10011,00111]]".
通过将 的每个元素本身编码为三位二进制字符串,
我们可以将任意对象集合 的表示转换为一种表示, 使得可以表示这些对象的(潜在嵌套)列表.
2.5.9 一些注释
我们通常会将一个对象与其字符串表示等同起来.
例如, 如果 是某个将字符串映射到字符串的函数, 且 是一个整数, 我们可能会说 “ 是质数”, 这意味着如果我们将 表示为字符串 那么由字符串 表示的整数 满足 是质数.
(你可以看到, 这种将对象与其表示等同的约定可以为我们节省大量繁琐的形式化表达.)
同样地, 如果 是某些对象, 且 是一个以字符串为输入的函数, 那么 表示将 应用于有序对 的表示的结果.
我们对任意 元组对象使用相同的符号表示函数的调用.
这种将对象与其字符串表示等同的约定, 是我们人类一直在使用的.
例如, 当人们说 “ 是质数” 时, 他们真正的意思是, 十进制表示为字符串 “17” 的整数是质数.
当我们说
“ 是一个计算自然数乘法的算法”
时, 我们真正的意思是
“ 是一个计算函数 的算法, 满足对于每一对 如果 是表示有序对 的字符串, 那么 将是表示它们乘积 的字符串”.
天呐!
2.6 将计算任务定义为数学函数
抽象地讲, 计算过程 是一种将输入(二进制字符串)转换为输出(二进制字符串)的过程.
这种从输入到输出的变换可以通过现代计算机、遵循指令的人、某些自然系统的演化或其他任何手段完成.
在后续章节中, 我们将转向对计算过程的数学定义, 但正如上文所讨论的, 目前我们关注 计算任务. 也就是说, 我们关注的是 规范 而非 实现.
同样地, 在抽象层面上, 一个计算任务可以指定输出需要满足的任意输入输出关系.
然而, 在本书的大部分内容中, 我们将专注于最简单、最常见的任务: 计算函数.
下面是一些例子:
- 给定两个整数 的表示, 计算它们的乘积 使用上面的表示方法, 这对应于从 到 的函数计算. 我们已经看到, 解决这个计算任务的方法不止一种, 事实上, 我们仍然不知道该问题的最优算法.
- 给定一个整数 的表示, 计算其 因式分解; 即, 找出质数列表 使得 这同样对应于从 到 的函数计算. 对于该问题的复杂性, 我们的认知差距甚至更大.
- 给定图 的表示和两个顶点 与 计算 中从 到 的最短路径长度, 或者计算从 到 的 最长路径(不重复顶点)的长度. 这两个任务都对应于从 到 的函数计算, 但它们的计算难度却差别极大.
- 给定一个 Python 程序的代码, 判断是否存在输入会使程序进入无限循环. 该任务对应于从 到 的 部分函数 计算, 因为并非每个字符串都对应语法有效的 Python 程序. 我们会看到, 我们 确实 理解该问题的计算状态(见下文的状态机), 但答案相当令人惊讶.
- 给定图像 的表示, 判断 是猫的照片还是狗的照片. 这对应于从 到 的某个(部分)函数的计算.
计算任务的一个重要特例是计算 布尔函数, 其输出为单比特
计算这类函数对应于回答 是/否 问题, 因此该任务也被称为 判定问题.
给定任意函数 和 计算 的任务对应于判定 是否属于集合 其中 被称为与函数 对应的 语言.(语言这个术语源于计算理论与诺姆·乔姆斯基发展的形式语言学之间的历史联系.)
因此, 许多文献将这类计算任务称为 判定一个语言.
对于每一个特定函数 可能存在多种 算法 来计算
我们将关注如下问题:
- 对于给定函数 是否可能 不存在算法 来计算 ?
- 如果存在算法, 哪一个是最优的? 是否可能 在某种意义上是 “有效不可计算“的, 即计算 的每个算法都需要极其庞大的资源?
- 如果我们无法回答这个问题, 能否在不同函数 和 之间证明某种等价性, 即它们要么都容易(有快速算法), 要么都困难?
- 一个函数难以计算是否可能是 好事? 我们能否将其应用于密码学等领域?
为了回答这些问题, 我们需要对 算法 的概念进行数学定义, 这将在 第三章 中完成.
2.6.1 注意区分 函数 和 程序!
你应始终注意 规范 与 实现 之间可能产生的混淆, 或等价地, 数学函数 与 算法/程序 之间的混淆.
编程语言(包括 Python)使用 函数 这个术语来表示(部分)程序, 这只会增加混乱.
这种混淆还源于数千年的数学历史, 在历史上人们通常通过一种计算方法来定义函数.
例如, 考虑自然数上的乘法函数.
这是函数 将一对自然数 映射为它们的乘积
正如我们提到的, 它可以通过多种方式实现:
def mult1(x,y):
res = 0
while y>0:
res += x
y -= 1
return res
def mult2(x,y):
a = str(x) # represent x as string in decimal notation
b = str(y) # represent y as string in decimal notation
res = 0
for i in range(len(a)):
for j in range(len(b)):
res += int(a[len(a)-i])*int(b[len(b)-j])*(10**(i+j))
return res
print(mult1(12,7))
# 84
print(mult2(12,7))
# 84
无论是 mult1 还是 mult2, 给定相同的自然数输入对, 都会产生相同的输出.
(不过当数字变大时, mult1 所需时间会长得多.)
因此, 尽管它们是两个不同的 程序, 它们计算的是相同的 数学函数.
区分 程序或算法 与 计算的函数 对本课程至关重要 (参见 图 2.13).
区分 函数 与 程序(或其他计算方式, 包括 电路 和 机器)是本课程的一个核心主题.
因此, 这也是我(以及许多其他教师)在作业和考试中经常提出的问题主题(暗示一下, 暗示一下).
备注 2.7 (超越于函数的计算 (进阶主题, 选读)).
函数能够涵盖相当多的计算任务, 但我们也可以考虑更一般的情形.
首先, 我们可以且将要讨论 部分函数, 它们并不在所有输入上都有定义.
在计算部分函数时, 我们只需关注函数定义域内的输入.
换句话说, 我们可以在假设有人“承诺“所有输入 都使得 有定义的前提下, 设计部分函数 的算法(否则我们不关心结果).
因此, 这种任务也被称为 承诺问题 (promise problems).
另一种推广是考虑 关系, 它可能有多个可接受的输出.
例如, 考虑求解给定方程组的任意解的任务.
一个 关系 将字符串 映射为一个 字符串集合 (例如, 可能描述一组方程, 此时 对应于 的所有解的集合).
我们也可以将关系 与字符串对 的集合对应起来, 其中
如果一个计算过程对于每个 都输出某个 则称它求解了关系
在本书后续章节, 我们将考虑更一般的任务, 包括 交互式任务(如在游戏中寻找良好策略)、使用概率概念定义的任务等.
然而, 在本书的大部分内容中, 我们将专注于 计算函数 的任务, 并且常常是 布尔函数, 输出仅为单比特.
事实证明, 在这个任务背景下可以研究大量计算理论, 所获得的见解在更一般的情形中同样适用.
- 我们可以使用二进制字符串来表示希望计算的对象.
- 一个集合 的表示方案是从 到 的一一映射.
- 我们可以使用前缀无关编码将集合 的表示“升级“为集合中元素列表的表示.
- 一个基本的计算任务是 计算函数 的任务. 这个任务不仅包括乘法、因式分解等算术计算, 还涵盖了科学计算、人工智能、图像处理、数据挖掘等众多领域中的其他任务.
- 我们将研究如何找到(或至少给出界限)计算各种有趣函数 的 最优算法 的问题.
2.7 习题
习题 2.1.
以下哪个对象可以用二进制字符串表示?
a. 一个整数
b. 一个无向图
c. 一个有向图
d. 以上所有
习题 2.2 (二进制表示). a. 证明在 (2.1) 中定义的二进制表示函数 满足对于每个 如果 那么 且
b. 给出一个函数 使得对于每个 都有 从而证明 是一个单射函数.
习题 2.3 (更加紧凑的ASCII表示). ASCII 编码可以将由 个英文字母组成的字符串编码为一个 位的二进制字符串, 但在本练习中, 我们要求为小写英文字母字符串寻找一种更紧凑的表示方法.
-
证明存在一种表示方案 用于将字母表 (共 26 个字母)上的字符串编码为二进制字符串, 使得对于每个 和长度为 的字符串 表示 是一个长度不超过 的二进制字符串. 换言之, 证明对于每个 存在一个单射函数
-
证明不存在一种表示方案, 用于将字母表 上的字符串编码为二进制字符串, 使得对于每个长度为 的字符串 表示 是一个长度为 的二进制字符串. 换言之, 证明存在某个 使得不存在单射函数
-
Python 的
bz2.compress函数是一个从字符串到字符串的映射, 它使用无损(因此是单射)的 bzip2 算法进行压缩. 在转换为小写并截去空格和数字后, 托尔斯泰的《战争与和平》文本包含 个字符. 然而, 如果我们对《战争与和平》的文本字符串运行bz2.compress, 会得到一个长度为 位的字符串, 这只有 (尤其远小于 解释为什么这不与你对前一个问题的回答相矛盾. -
有趣的是, 如果我们尝试对随机字符串应用
bz2.compress, 性能会差得多. 在我的实验中, 输出位数与输入字符数之间的比率约为 然而, 有人可能会想象可以做得更好, 并且存在一家名为“Pied Piper”的公司, 其算法可以将由 个随机小写字母组成的字符串无损压缩到少于 位. 5 通过证明对于每个 和单射函数 如果我们令 为随机变量 (即 的长度), 其中 是从集合 中均匀随机选择的, 则 的期望值至少为 来说明这种情况不可能发生.
习题 2.7. 假设 对应于将一个数 表示为一个由 个 1 组成的字符串( 例如, 等). 如果 和 是介于 和 之间的数, 那么当以 表示形式给出它们时, 我们是否仍然能用 次操作将 和 相乘?
习题 2.8. 回忆一下, 如果 是一个一一对应且满射的函数, 将有限集 中的元素映射到有限集 那么 和 的大小相同. 令 是一个函数, 使得对于每个 是 的二进制表示.
证明 当且仅当
使用第1题来计算集合 的大小, 其中 表示字符串 的长度.
使用第1题和第2题来证明
习题 2.10 (更高效的前缀无关转换). 假设 是集合 中对象的一种表示法( 不一定前缀无关), 且 是自然数的一种前缀无关表示法. 定义 ( 即, 将 的长度的表示与 本身连接起来).
a. 证明 是 的一种前缀无关表示法.
b. 证明我们可以通过一种修改将任何表示法转换为前缀无关的表示法, 该修改将一个 位字符串转换为长度至多为 的字符串.
c. 证明我们可以通过一种修改将任何表示法转换为前缀无关的表示法, 该修改将一个 位字符串转换为长度至多为 的字符串. 6
- 我们已经证明了自然数可以表示为字符串. 证明反方向也成立: 存在一个一对一映射 ( 表示“字符串到数字”. )
- 回忆一下, Cantor 证明了不存在一对一映射 证明 Cantor 的结果蕴含 定理 2.1.
2.8 参考书目
将数据表示为字符串的研究( 包括 压缩 和 纠错 等问题)属于 信息论 的范畴, 这在 Cover 和 Thomas 的经典教材 (Cover, Thomas, 2006) 中有涵盖. 表示法也在 数据结构设计 领域中被研究, 相关教材如 (Cormen, Leiserson, Rivest, Stein, 2009).
关于用最高有效位在前还是在后表示整数的问题, 被称为大端序与小端序表示法. 这一术语来源于 Cohen 的 (Cohen, 1981) 那篇兼具趣味性与知识性的论文, 他在文中将两派拥护者之间的冲突比作乔纳森·斯威夫特的《格列佛游记》中交战不休的部落. 有符号整数的二进制补码表示法是在冯·诺依曼的经典报告 (von Neumann, 1945) 中提出的, 该报告详细阐述了存储程序计算机的设计方案, 不过类似的表示法甚至更早就在算盘和其他机械计算设备中得到了使用.
我们应当将函数的 定义 或 规范 与其 实现 或 计算 分离开来, 这一想法看似“显而易见“, 但数学家们花了相当长的时间才达成这一观点. 历史上, 函数 是通过展示如何从输入推导出输出的规则或公式来标识的. 正如我们在第9章中更深入讨论的那样, 在 19 世纪, 这种有些非正式的函数概念开始“出现裂痕“, 最终数学家们得出了更严谨的定义, 即函数是输入到输出的任意赋值. 虽然许多函数可以通过一个或多个公式来描述( 或计算), 但如今我们并不认为这是函数的基本属性, 也允许存在不对应于任何“优美“公式的函数.
我们已经提到, 实数的所有表示法本质上都是 近似的. 因此, 一项重要的努力是理解, 我们能够就算法输出的近似质量提供何种保证, 并将其作为输入近似质量的函数. 这个问题被称为确定给定方程的数值稳定性的问题. 浮点数指南网站 详细描述了浮点数表示法及其可能微妙失效的多种方式, 另请参阅网站 0.30000000000000004.com.
Dauben (Dauben, 1990) 撰写了康托尔的传记, 重点介绍了他的数学思想发展历程. (Halmos, 1960) 是一本关于集合论的经典教材, 也包括了康托尔定理. 康托尔定理也在许多离散数学教材中有所涵盖, 包括 (Meyer, 2018)(Lewis, Zax, 2019).
图的邻接矩阵表示法不仅仅是将图映射成二进制字符串的便捷方法, 而且事实证明, 矩阵的许多自然概念和运算对图也很有用. ( 例如, 谷歌的 PageRank 算法就依赖于这一观点. )Spielman 课程 的笔记是这个领域( 称为 谱图论 )的极佳资源. 我们将在本书后面讨论 随机游走 时, 重新回到这一观点.
1: 尽管巴比伦人早已发明了位置记数法, 我们今天使用的十进制位置记数法是印度数学家约在公元三世纪发明的, 再由阿拉伯数学家在八世纪采用与发展. 它在欧洲首次受到显著关注是在 1202 年 Fibonacci(又名 Leonardo of Pisa)出版的著作 “Liber Abaci” 中, 但直到十五世纪, 它才在日常使用中取代罗马数字.
2: 其中 代表 “real numbers to strings”.
3: 代表 “functions to strings”.
4: 代表 “functions to reals”.
5: 实际上, 这家虚构公司使用的指标更关注压缩速度而非压缩率, 参见这里和这里.
6: 提示: 递归地思考如何表示字符串的长度.