Warning

本章施工中

通用性和不可计算性

通用性和不可计算性

学习目标

通用机器/程序: “以一驭万“的单一程序
计算机科学与数学的基础结论: 不可计算函数的存在性
停机问题: 不可计算函数的典型范例
了解归约(reduction)这一技巧
RIce定理: 不可计算性研究的“元工具“, 亦是编译器, 编程语言与软件验证领域众多研究的起点

“变量函数是由该变量与数字或常量以任意方式组合而成的解析表达式. “

——Leonhard Euler, 1748年

“通用机器的重要性显而易见. 我们无需制造无数台执行不同任务的机器……生产各类专用机器的工程问题, 已被为通用机器’编程’这类文书工作所取代. “

——Alan Turing, 1948年

我们在布尔电路(或等价的直线程序)研究中取得的最重要成果之一即是通用性(universality)这一概念: 存在可运行所有其他电路的单一电路. 然而该结论存在重要限制:运行包含 $s$ 个门电路的电路时, 通用电路所需门电路数量必须大于 $s .$ 事实证明, 图灵机或NAND-TM程序等均匀计算模型能帮助我们“突破此循环“, 并真正实现能运行所有其他机器的通用图灵机(universal turing machine) $U,$ 其甚至能处理比 $U$ 自身更复杂(如具备更多状态)的机器. (同理, 存在能运行所有NAND-TM程序的通用NAND-TM程序(universialNAND-TMprogram) $U^{'},$ 包括那些比 $U^{'}$ 具有更多代码行的程序)

可以毫不夸张地说, 此类通用程序/机器的存在奠定了二十世纪后半叶(并持续至今)的信息技术革命根基. 在此之前的漫长历史中, 人类虽创造了诸如算盘, 计算尺及各类三角级数计算装置等专用计算设备, 但正如图灵(或许是最早洞见通用性的深远影响的思想家)所指出的, 通用计算机具有更强大的潜力. 当我们构建出能计算单一通用函数的设备后, 便获得了通过软件扩展其实现任意计算的能力. 例如要模拟新图灵机 $M$ 时, 无需重新构建实体机器, 只需将 $M$ 表示为字符串(即代码)并输入至通用机器 $U$ 即可.

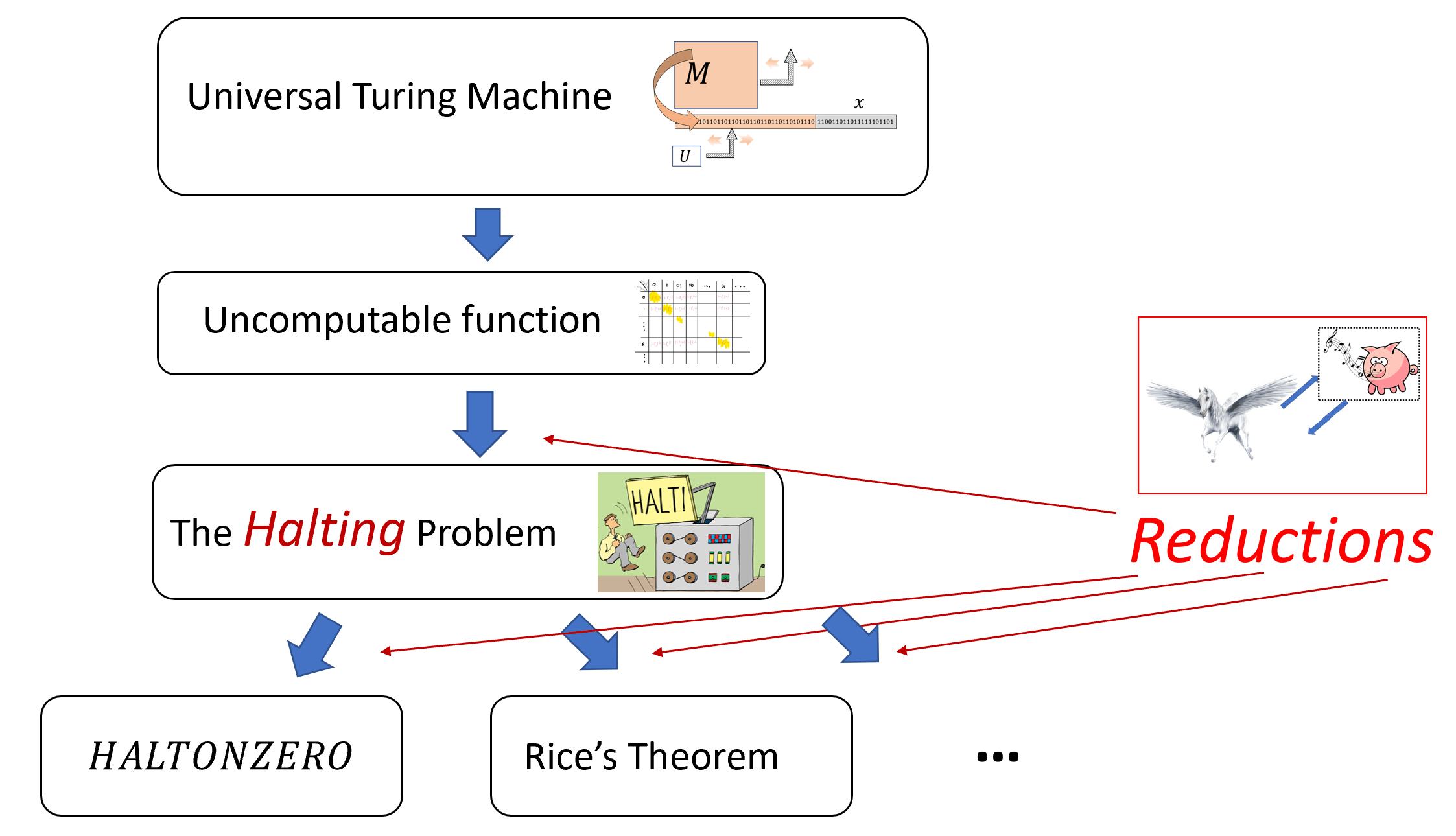
除实际应用外, 通用算法的存在更具深远的理论意义, 尤其可用于证明不可计算函数(uncomputable functions)的存在, 此举颠覆了自Euler至Hilbert等数学家数百年来形成的数学直觉. 本章将论证通用程序的存在性, 并阐释其对不可计算性研究的启示, 详见图 9.1.

简要概述

本章将展现计算机科学中的两项重大成果:

通用图灵机的存在性: 可运行所有其他算法的单一算法
不可计算函数的存在性: 任何算法都无法计算的函数(包括著名的“停机问题“)

我们将通过归约(reductions)技巧论证函数计算的困难性. 归约是借助“假想“能力(假设某函数可被计算)来推导其他函数计算途径的方法. 该技术当然广泛运用于编程领域:我们常将某些任务作为“黑箱“子程序来构建其他任务的算法. 但本章将采用“逆否“视角: 不再通过归约证明前项任务的“简易性“, 而是用以揭示后项任务的“困难性“. 如果你觉得归约费解无需担忧, 这一概念需要时日与实践方能掌握.

universalchapoverviewfig

图 9.1. 本章将证明通用图灵机的存在, 据此推导出某些不可计算函数的存在性, 进而揭示图灵著名“停机问题“(即 $HALT$ 函数)的不可计算性, 并引申出诸多不可计算性结论. 我们同时引入归约方法, 通过函数F的不可计算性推导新函数 $G$ 的不可计算性.

9.1 通用性或自循环解释器

我们首先证明通用图灵机的存在性. 这是一个独立的图灵机 $U,$ 能够模拟任意图灵机 $M$ 在任意输入 $x$ 上的运行, 甚至包括那些状态数和字母表规模都超过 $U$ 本身的图灵机 $M .$ 特别地, $U$ 甚至可以用来运行自身! 这种自指(self reference)概念将在本书中反复出现, 并且正如我们将要看到的, 它会引发计算领域中诸多反直觉的现象.

定理 9.1 (通用图灵机).

存在一个图灵机 $U,$ 使得对于每个表示图灵机的字符串 $M$ 以及任意 $x \in {0, 1}^{*},$ 满足 $U (M, x) = M (x) .$

即若机器 $M$ 在输入 $x$ 上停机并输出某个 $y \in {0, 1}^{*},$ 则 $U (M, x) = y;$ 若 $M$ 在 $x$ 上不停机(即 $M (x) = ⊥),$ 则 $U (M, x) = ⊥.$

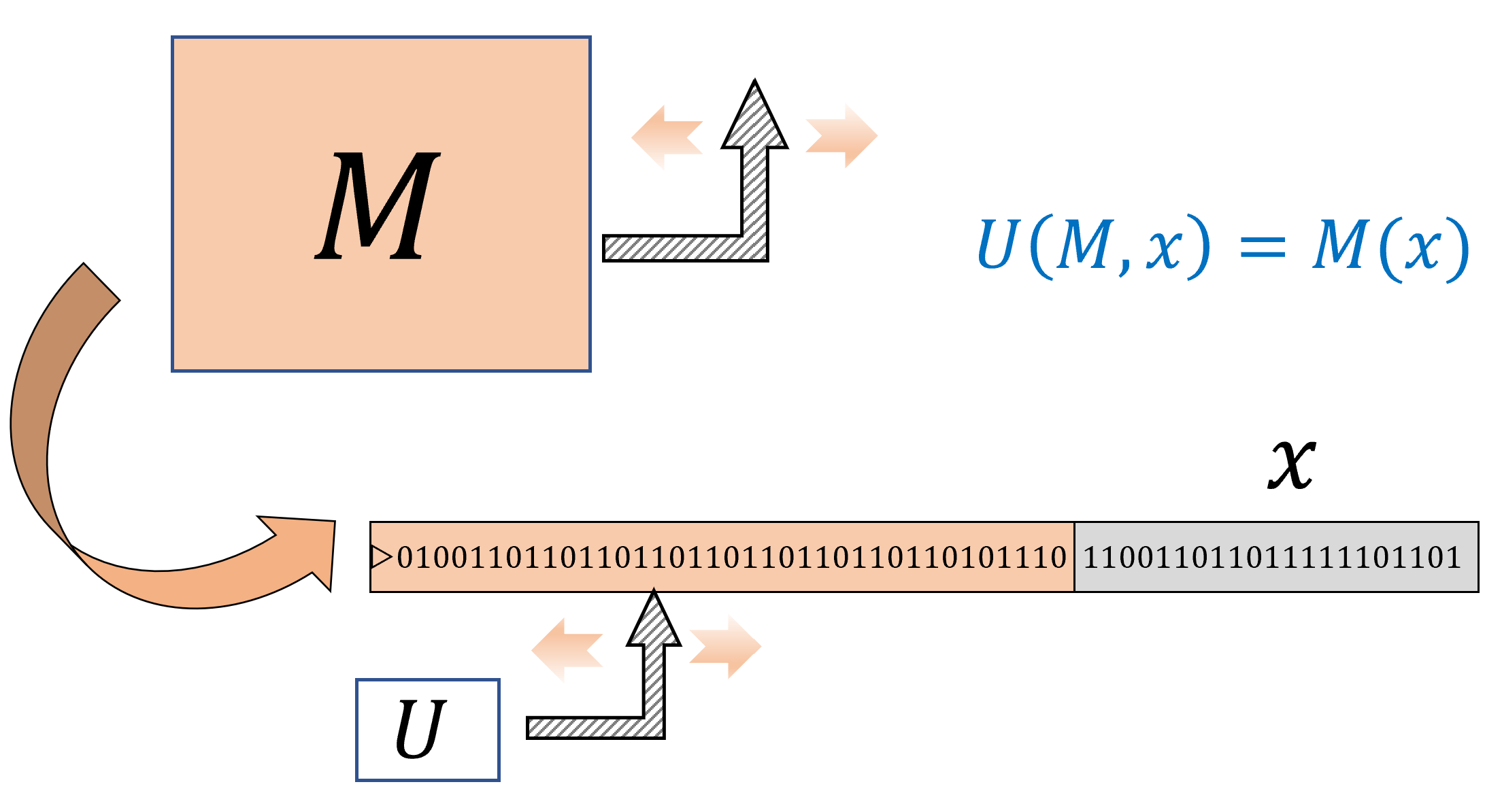
universaltmfig

图 9.2. 通用图灵机是一个独立的图灵机 $U,$ 当输入任意图灵机 $M$ (以字符串形式描述)及其输入 $x$ 时, 能够计算 $M$ 在 $x$ 上的输出. 与图5.6所示的通用电路不同, 机器 $M$ 可以比 $U$ 复杂得多(例如具有更多状态或磁带字母符号).

重要启示

重要提示 9.1.

存在一种“通用“算法, 能够在任意输入上运行任意算法.

定理 9.1的证明思路

只要理解定理的含义, 证明并不困难. 目标程序 $U$ 本质上是图灵机的解释器: 它获取机器 $M$ 的表述(可视为源代码)和输入 $x,$ 通过模拟执行 $M$ 在 $x$ 上的运算过程.

设想如何用常用编程语言实现 $U :$ 首先需要设计 $M$ 的编码方案(例如用数组或字典表示状态转移函数), 随后使用链表等数据结构存储 $M$ 的磁带内容, 逐步模拟 $M$ 的运行并动态更新数据. 解释器将持续模拟直至机器停机.

接下来只需依照第8章的方法, 将该解释器从编程语言转化为图灵机. 最终得到的就是“自循环解释器“(meta-circular evaluator), 即用同一语言实现该语言的解释器. 这一概念自通用图灵机诞生伊始便贯穿计算机科学史, 亦可参见图 9.3的示意.

9.1.1 证明通用图灵机的存在性

为证明(甚至准确表述)定理 9.1, 我们需要确定一种将图灵机表示为字符串的编码方式. 一种可能的方案是利用图灵机与NAND-TM程序的等价性, 从而用对应NAND-TM程序 $P$ 源代码的ASCII编码来表示图灵机 $M .$ 但我们将采用更直接的编码方式.

定义 9.1 (图灵机的字符串表示).

设 $M$ 是一个具有 $k$ 个状态, 字母表 $Σ = {σ_{0}, \dots, σ_{ℓ - 1}}$ (遵循 $σ_{0} = 0,$ $σ_{1} = 1,$ $σ_{2} = \emptyset,$ $σ_{3} = ▹$ 的约定)的图灵机. 我们将 $M$ 表示为三元组 $(k, ℓ, T),$ 其中 $T$ 是 $δ_{M}$ 的函数值表:

$T = (δ_{M} (0, σ_{0}), δ_{M} (0, σ_{1}), \dots, δ_{M} (k - 1, σ_{ℓ - 1})),$

这里每个 $δ_{M} (s, σ)$ 的值是一个三元组 $(s^{'}, σ^{'}, d),$ 其中 $s^{'} \in [k],$ $σ^{'} \in Σ,$ $d$ 是编码 ${L, R, S, H}$ 中某个方向的数字 ${0, 1, 2, 3} .$ 因此这类图灵机 $M$ 可由包含 $2 + 3 k \cdot ℓ$ 个自然数的列表编码. $M$ 的字符串表示是由通过连接这些整数的前缀无关编码获得. 若字符串 $α \in {0, 1}^{*}$ 不符合上述整数列表形式, 则视其表示一个在任意输入上立即停机的单状态平凡图灵机.

Info

备注 9.1 (表示方法的要点).

将图灵机编码为字符串的具体细节在绝大多数应用中并不重要. 只需牢记以下要点:

每个图灵机都可表示为字符串.
给定图灵机 $M$ 的字符串表示和输入 $x,$ 我们可以模拟 $M$ 在输入 $x$ 上的运行过程(这是定理 9.1的核心内容).

另一个细节是为了方便起见, 我们假设每个字符串都表示某个图灵机. 通过将不符合要求的字符串映射到某个固定的平凡图灵机, 很容易满足这一假设. 该假设虽不重要, 但能使某些结论(如Rice定理: 定理 9.7)的表述更简洁.

利用此表示法, 我们可以严格证明定理 9.1.

定理 9.1的证明

此处仅概述证明的主要思路. 首先注意到我们可以轻松编写一个Python程序, 该程序根据图灵机 $M$ 的表示 $(k, ℓ, T)$ 和输入 $x,$ 在 $X$ 上对 $M$ 进行求值. 以下是该程序的具体代码(若不熟悉或不感兴趣可跳过):

# constants
def EVAL(δ,x):
    '''Evaluate TM given by transition table δ
    on input x'''
    Tape = ["▷"] + [a for a in x]
    i = 0; s = 0 # i = head pos, s = state
    while True:
        s, Tape[i], d = δ[(s,Tape[i])]
        if d == "H": break
        if d == "L": i = max(i-1,0)
        if d == "R": i += 1
        if i>= len(Tape): Tape.append('Φ')

    j = 1; Y = [] # produce output
    while Tape[j] != 'Φ':
        Y.append(Tape[j])
        j += 1
    return Y

在输入转移表 $δ$ 时, 该程序将逐步模拟对应图灵机 $M$ 的运行过程, 始终维持数组Tape包含 $M$ 的磁带内容, 变量s包含 $M$ 当前状态的不变性.

上述内容并未完全证明定理, 因为我们需要展示计算 $EVAL$ 的是图灵机而非Python程序. 通过足够努力, 我们可以将此Python代码逐行转换为图灵机. 但为证明定理, 我们无需实际完成这一转换, 而是可以运用“鱼与熊掌兼得”范式: 虽然需要运行图灵机, 但在编写解释器代码时允许使用更强大的模型(如NAND-RAM), 因为根据定理8.1, 其与图灵机在计算能力上等价.

将上述Python代码转换为NAND-RAM程序非常直接. 唯一的问题是NAND-RAM没有内置存储转移函数δ的字典数据结构. 但我们可以将形如 ${k e y_{0} : v a l_{0}, \dots, k e y_{m - 1} : v a l_{m - 1}}$ 的字典 $D$ 表示为简单的键值对列表. 通过扫描所有键值对直到找到 $(k, v)$ 形式, 即可计算 $D [k] .$ 类似地, 通过扫描列表并修改或追加 $(k ey, v a l)$ 键值对, 即可更新字典.

Info

备注 9.2 (模拟的效率).

定理 9.1证明中实现字典数据结构的方式在实践中效率很低, 但足以满足证明目的. 这种实现方式下对包含 $m$ 个值的字典进行读写需要 $Ω (m)$ 步, 但实际使用搜索树数据结构可在 $O (lo g m)$ 步内完成, 甚至通过哈希表在“典型”情况下仅需 $O (1)$ 步. NAND-RAM和RAM机器对应现代电子计算机架构, 因此我们可以在NAND-RAM中实现哈希表和搜索树, 就像在其他编程语言中实现那样.

上述构造产生的通用图灵机具有非常多的状态. 但由于通用图灵机具有重要的哲学和技术意义, 研究人员一直致力于寻找最小的通用图灵机(见第9.7节).

9.1.2 通用性的影响(讨论)

lispinterpreterfig

图 9.3. a) “元循环求值器”的一个特别优雅的示例来自John McCarthy在1960年的论文, 他在定义Lisp编程语言时给出了一个可求值任意Lisp程序的Lisp函数(见上图). Lisp最初并非作为实用编程语言设计, 此示例旨在说明Lisp通用函数比通用图灵机更优雅. 但麦卡锡的研究生史蒂夫·罗素建议将其实现. 据麦卡锡后来回忆: “我对他说, 呵呵, 你把理论和实践搞混了, 这个eval函数是用来阅读而不是计算的. 但他坚持做了下去——他将我论文中的eval编译成IBM 704机器码, 修复了一个错误, 然后将其作为Lisp解释器发布, 这确实名副其实. ” b) 汤普逊的经典论文(Thompson, 1984)中的自复制C程序.

满足定理 9.1条件的图灵机 $U$ 不止一个, 但即使仅存在一个这样的机器, 对计算机科学的理论与实践都具有极其重要的意义. 定理 9.1的影响超越了图灵机这一特定模型. 由于每个图灵机都可以被NAND-TM程序模拟, 反之亦然, 定理 9.1直接表明存在通用NAND-TM程序 $P_{U}$ 使得 $P_{U} (P, x) = P (x)$ 对每个NAND-TM程序 $P$ 成立. 我们还可以“混合搭配”不同模型: 由于每个NAND-RAM程序可被图灵机模拟, 每个图灵机可被 $λ$ 演算模拟, 定理 9.1表明存在 $λ$ 表达式 $e,$ 使得对每个满足 $P (x) = y$ 的NAND-RAM程序 $P$ 和输入 $x,$ 若将 $(P, x)$ 编码为 $λ$ 表达式 $f$ (使用 $λ$ 演算将字符串编码为0和1的列表), 则 $(e f)$ 会求值为 $y$ 的编码. 更一般地说, 对于图灵等价模型集合{图灵机, RAM机器, NAND-TM, NAND-RAM, $λ$ 演算, JavaScript, Python……}中的任意 $X$ 和 $Y,$ 都存在 $X$ 中的程序/机器, 可计算每个程序/机器 $P \in Y$ 的映射关系 $(P, x) \mapsto P (x) .$

“通用程序”的思想当然不仅限于理论. 例如编程语言的编译器常被用于编译自身以及比编译器更复杂的程序(Fabrice Bellard的Obfuscated Tiny C编译器就是典型例子: 这个2048字节的C程序能编译C编程语言的一个大型子集, 尤其能编译自身). 这也与可打印自身源代码的程序相关(见图 9.3). 目前已知存在需要极少状态或字母符号的通用图灵机, 特别是存在一种(基于特定图灵机字符串表示方法的)通用图灵机, 其磁带字母表为 ${▹, \emptyset, 0, 1}$ 且状态数少于25个(见第9.7节).

9.2 所有函数都可计算吗?

在定理4.6中, 我们看到NAND-CIRC程序可以计算每个有限函数 $f : {0, 1}^{n} \to {0, 1} .$ 因此, 一个很自然的猜想是, NAND-TM程序(或者等价地说, 图灵机)能够计算每个无限函数 $F : {0, 1}^{*} \to {0, 1} .$ 然而, 事实并非如此. 也就是说, 存在一个函数 $F : {0, 1}^{*} \to {0, 1}$ 是不可计算的!

不可计算函数的存在是相当令人惊讶的. 我们对“函数“的直观概念(也是直到20世纪大多数数学家所持有的概念)是, 函数 $f$ 定义了某种从输入 $x$ 计算输出 $f (x)$ 的隐式或显式方法. 因此, “不可计算函数“这个概念看起来似乎自相矛盾, 但下面的定理表明, 这样的函数确实存在:

定理 9.2 (不可计算函数).

存在一个函数 $F^{*} : {0, 1}^{*} \to {0, 1},$ 它不能被任何图灵机计算.

定理 9.2的证明思路

证明背后的思路与康托尔证明实数是不可数(定理2.2)的思路非常接近, 实际上, 这个定理也可以相当直接地从那个结果推导出来(见练习7.11). 然而, 看看直接证明是有启发性的. 思路是构造 $F^{*}$ 的方式将确保每一台可能的机器 $M$ 实际上都无法计算 $F^{*} .$ 我们通过如下方式实现: 如果 $x$ 描述了一台满足 $M (x) = 1$ 的图灵机 $M,$ 则定义 $F^{*} (x)$ 等于 $0;$ 否则定义 $F^{*} (x) = 1.$ 根据构造, 如果 $M$ 是任意图灵机且 $x$ 是描述它的字符串, 那么 $F^{*} (x) \neq = M (x),$ 因此 $M$ 不能计算 $F^{*} .$

定理 9.2的证明

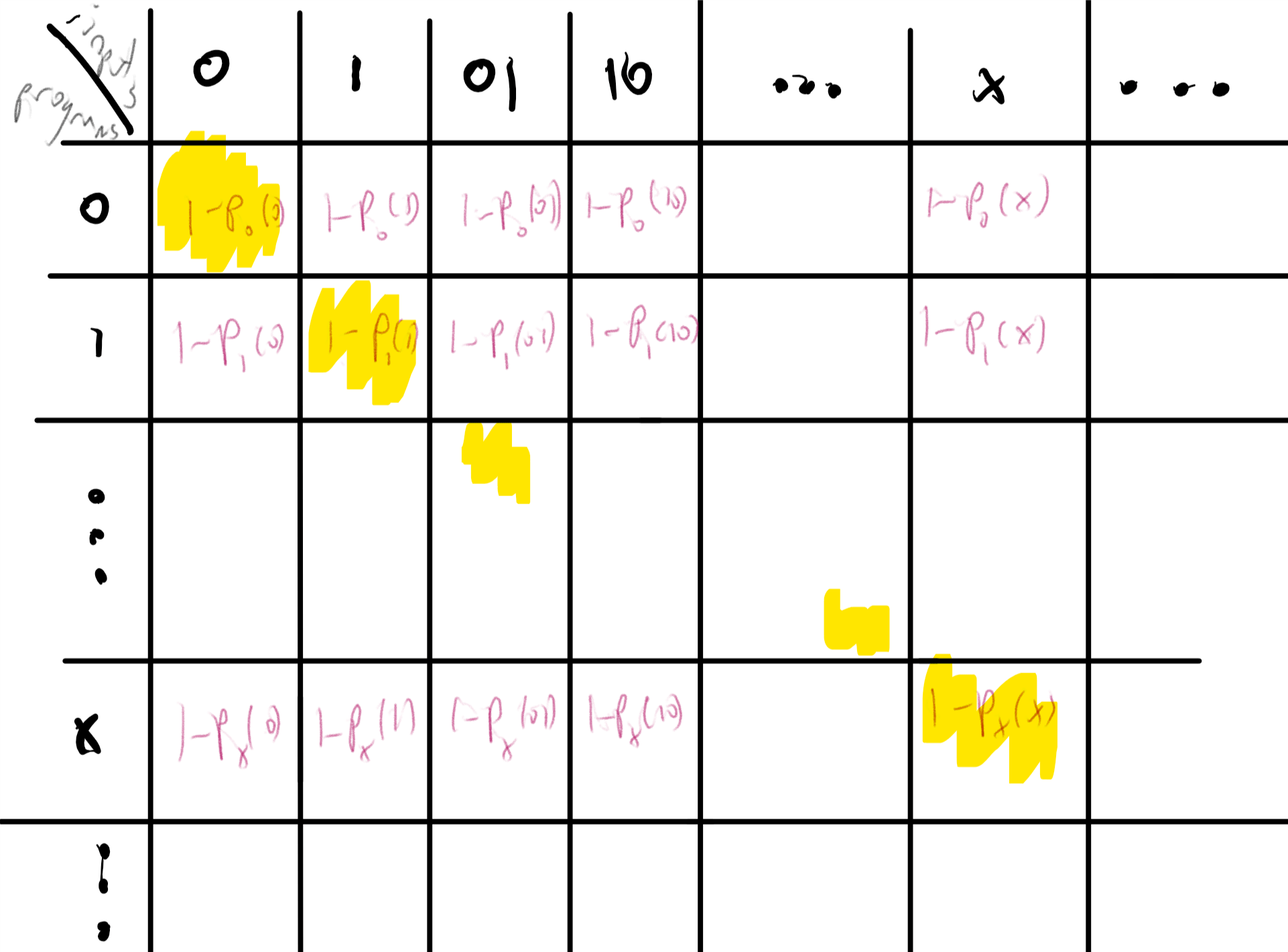
证明过程如图 9.4所示. 我们首先定义以下函数 $G : {0, 1}^{*} \to {0, 1} :$

对于每个字符串 $x \in {0, 1}^{*},$ 如果 $x$ 满足**(1) $x$ 是某个图灵机 $M$ 的有效表示(根据上述表示方案), 并且(2)**当程序 $M$ 在输入 $x$ 上执行时它停机并产生一个输出, 那么我们将 $G (x)$ 定义为此输出的第一个比特. 否则(即, 如果 $x$ 不是图灵机的有效表示, 或者机器 $M_{x}$ 在 $x$ 上永不停机), 我们定义 $G (x) = 0.$ 我们定义 $F^{*} (x) = 1 - G (x) .$

我们声称不存在计算 $F^{*}$ 的图灵机. 确实, 假设为了推出矛盾, 存在一台机器 $M$ 计算 $F^{*},$ 并令 $x$ 是表示机器 $M$ 的二进制字符串. 一方面, 根据我们的假设, $M$ 计算 $F^{*},$ 在输入 $x$ 上, 机器 $M$ 停机并输出 $F^{*} (x) .$ 另一方面, 根据 $F^{*}$ 的定义, 由于 $x$ 是机器 $M$ 的表示, $F^{*} (x) = 1 - G (x) = 1 - M (x),$ 从而产生矛盾.

diagonal-fig

图 9.4. 我们通过为每对字符串 $x, y$ 定义值 $1 - M_{y} (x)$ 来构造一个不可计算函数, 如果由 $y$ 描述的机器在 $x$ 上输出 $1,$ 则该值为 $0,$ 否则为 $1.$ 然后我们定义 $F^{*} (x)$ 为该表的“对角线“, 即对每个 $x,$ $F^{*} (x) = 1 - M_{x} (x) .$ 函数 $F^{*}$ 是不可计算的, 因为如果它可由某个字符串描述为 $x^{*}$ 的机器计算, 那么我们将得到 $M_{x^{*}} (x^{*}) = F^{*} (x^{*}) = 1 - M_{x^{*}} (x^{*}) .$

重要启示

重要提示 9.2.

存在一些函数是任何算法都无法计算的.

暂停一下

定理 9.2的证明简短但精妙. 我建议你在这里暂停, 回头再读一遍并思考一下——这是一个值得读至少两遍, 如果不是三四遍的证明. 用几行数学推理就确立了一个意义深远的事实——即存在我们根本无法解决的问题——这种情况并不常见.

用于证明定理 9.2的论证类型被称为对角线法, 因为它可以像图 9.4中那样, 被描述为基于表的对角线项来定义一个函数. 这个证明可以看作是我们用于在定理5.3中证明NAND-CIRC程序下界的计数论证的无限版本. 也就是说, 我们证明了不可能用图灵机计算所有从 ${0, 1}^{*} \to {0, 1}$ 的函数, 仅仅因为这样的函数比图灵机要多.

如备注7.4所述, 许多文献使用“语言“术语, 因此如果函数 $F : {0, 1}^{*} \to {0, 1}$ 满足 $F (x) = 1 \leftrightarrow x \in L$ 是不可计算的, 则称集合 $L \subseteq {0, 1}^{*}$ 为不可判定或非递归语言.

9.3 停机问题

定理 9.2表明存在某个无法计算的函数. 但是, 这个函数是否等同于“森林中无人听闻其倒下的树“呢? 也就是说, 它或许是一个实际上没有人想要计算的函数. 事实证明, 确实存在一些自然的不可计算函数：

定理 9.3 (停机函数的不可计算性).

令 $HALT : {0, 1}^{*} \to {0, 1}$ 为如下函数：对于每个字符串 $M \in {0, 1}^{*},$ 如果图灵机 $M$ 在输入 $x$ 上停机, 则 $HALT (M, x) = 1;$ 否则 $HALT (M, x) = 0.$ 那么 $HALT$ 是不可计算的.

在着手证明定理 9.3之前, 我们注意到 $HALT$ 是一个非常自然, 人们会想要计算的函数. 例如, 可以将 $HALT$ 视为管理“应用商店“任务的一个特例. 也就是说, 给定某个应用程序的代码, 商店的守门员需要决定此代码是否足够安全以允许进入商店. 至少, 我们似乎应该验证该代码不会进入无限循环.

定理 9.3的证明思路

理解此证明的一种方式如下： $F^{*} 的不可计算性 + 通用性 = HALT 的不可计算性$ 也就是说, 我们将使用计算 $EVAL$ 的通用图灵机, 从定理 9.2所证明的 $F^{*}$ 的不可计算性, 推导出 $HALT$ 的不可计算性. 具体来说, 我们将采用反证法进行证明. 即, 我们将为了引出矛盾而假设 $HALT$ 是可计算的, 然后利用该假设, 连同定理 9.1中的通用图灵机, 推导出 $F^{*}$ 是可计算的, 这将与定理 9.2相矛盾.

重要启示

重要提示 9.3.

如果一个函数 $F$ 是不可计算的, 我们可以通过给出一种将计算 $F$ 的任务归约到计算 $H$ 的方法, 来证明另一个函数 $H$ 也是不可计算的.

定理 9.3的证明

该证明将使用先前已建立的结果定理 9.2. 回顾定理 9.2表明以下函数 $F^{*} : {0, 1}^{*} \to {0, 1}$ 是不可计算的：

$F^{*} (x) = {01 x (x) = 1 其他情况$ 其中 $x (x)$ 表示由字符串 $x$ 描述的图灵机在输入 $x$ 上的输出(按照通常约定, 如果此计算不停机, 则 $x (x) = ⊥) .$

我们将证明 $F^{*}$ 的不可计算性意味着 $HALT$ 的不可计算性. 具体来说, 我们将为了引出矛盾而假设存在一个能够计算 $HALT$ 函数的图灵机 $M,$ 并利用它来得到一个计算函数 $F^{*}$ 的图灵机 $M^{'} .$ (这被称为_归约_证明, 因为我们将计算 $F^{*}$ 的任务归约到了计算 $HALT$ 的任务. 根据逆否命题, 这意味着 $F^{*}$ 的不可计算性蕴含着 $HALT$ 的不可计算性)

确实, 假设 $M$ 是一个计算 $HALT$ 的图灵机. 算法 9.1描述了一个计算 $F^{*}$ 的图灵机 $M^{'} .$ (我们使用图灵机的“高层次“描述, 援引“鱼与熊掌兼得“范式, 见核心思想10)

我们断言算法 9.1计算了函数 $F^{*} .$ 确实, 假设 $x (x) = 1$ (因此 $F^{*} (x) = 0) .$ 在这种情况下, $HALT (x, x) = 1,$ 因此在我们假设 $M (x, x) = HALT (x, x)$ 的条件下, 值 $z$ 将等于 $1,$ 因此算法 9.1将设定 $y = x (x) = 1,$ 并输出正确的值 $0.$

假设否则 $x (x) \neq = 1$ (因此 $F^{*} (x) = 1) .$ 在这种情况下, 有两种可能性：

情况1：: 由 $x$ 描述的机器在输入 $x$ 上不停机(因此 $F^{*} (x) = 1) .$ 在这种情况下, $HALT (x, x) = 0.$ 由于我们假设 $M$ 计算 $HALT,$ 这意味着在输入 $x, x$ 上, 机器 $M$ 必须停机并输出值 $0.$ 这意味着算法 9.1将设定 $z = 0$ 并输出 $1.$
情况2：: 由 $x$ 描述的机器在输入 $x$ 上停机并输出某个 $y^{'} \neq = 1$ (因此 $F^{*} (x) = 0) .$ 在这种情况下, 由于 $HALT (x, x) = 1,$ 根据我们的假设, 算法 9.1将设定 $y = y^{'} \neq = 1,$ 从而输出 $1.$

我们看到在所有情况下, $M^{'} (x) = F^{*} (x),$ 这与 $F^{*}$ 不可计算的事实相矛盾. 因此, 我们对我们最初关于 $M$ 计算 $HALT$ 的假设得出了矛盾.

算法 9.1 ( $F^{*}$ 到 $HALT$ 的归约). $Input : x \in {0, 1}^{*} Output : F^{*} (x) # 假设图灵机 M_{HALT} 计算 HALT Let z \leftarrow M_{HALT} (x, x) # 假设 z = HALT (x, x) if (z = 0) return 1 endif Let y \leftarrow U (x, x) # U 是通用图灵机, 即 y = x (x) if (y = 1) return 0 endif return 1$

暂停一下

这又是一个值得多次阅读的证明. 停机问题的不可计算性是计算机科学的基本定理之一, 并且是我们后续将看到的许多研究的起点. 更好地理解定理 9.3的一个极好方法是仔细阅读9.3.2节, 该节给出了同一结果的另一种证明.

9.3.1 停机问题真的困难吗? (讨论)

许多人在初次看到定理 9.3的证明时, 第一反应是不敢相信. 也就是说, 虽然大多数人都相信这个数学结论, 但从直觉上看, 停机问题似乎并不真的那么困难. 毕竟, 不可计算性仅仅意味着 $HALT$ 无法被图灵机计算.

但程序员们似乎总能通过非正式或正式地论证其程序会终止, 来解决 $HALT$ 问题. 虽然他们的程序是用C或Python编写的, 而不是图灵机, 但这并无区别: 我们可以轻松地在这个模型与任何其他编程语言之间进行转换.

尽管每个程序员都曾遇到过无限循环, 但真的没有办法解决停机问题吗? 有些人声称, 只要他们足够努力地思考, 就能够判断任何给定的具体程序是否会终止. 甚至有人认为, 人类普遍具有这种能力, 因此人类天生就拥有优于计算机或其他由图灵机建模的事物的智能. ¹

我们目前最好的答案是, 确实没有办法解决 $HALT,$ 无论是使用Mac, 个人电脑, 量子计算机, 人类, 还是任何其他电子, 机械和生物设备的组合. 实际上, 这一断言正是Church-Turing论题的内容. 当然, 这并不意味着对于每一个可能的程序 $P,$ 判断 $P$ 是否进入无限循环都很困难. 有些程序甚至根本没有循环(因此显然会终止), 并且还有许多其他不那么平凡的程序示例, 我们可以证明它们永远不会进入无限循环(或者我们确信它们会进入这样的循环). 然而, 并不存在一种通用方法, 能够对任意程序 $P$ 判断它是否终止. 此外, 有一些非常简单的程序, 没有人知道它们是否会终止. 例如, 以下Python程序当且仅当哥德巴赫猜想为假时才会终止:

def isprime(p):
    return all(p % i for i in range(2,p-1))

def Goldbach(n):
    return any( (isprime(p) and isprime(n-p))
           for p in range(2,n-1))

n = 4
while True:
    if not Goldbach(n): break
    n+= 2

鉴于哥德巴赫猜想自1742年提出以来一直未被解决, 人类是否拥有任何神奇的能力来判断这个(或其他类似程序)是否会终止, 尚不清楚.

xkcdhaltingfig

图 9.5. SMBC对解决停机问题的看法.

9.3.2 $HALT$ 不可计算性的直接证明(可选)

事实证明, 我们可以结合定理 9.2和定理 9.3的证明思路, 给出后者的一个简短证明, 而不需要诉诸 $F^{*}$ 的不可计算性. 这个简短证明出现在1965年Christopher Strachey写给《计算机杂志》编辑的一封信中:

致《计算机杂志》编辑.

一个不可能的程序

先生:

程序员间流传的一个众所周知的民间传说认为, 不可能编写一个程序来检查任何其他程序, 并在所有情况下判断它运行时是会终止还是进入封闭循环. 我从未在出版物上见过此事的证明, 尽管Alan Turing曾给过我一个口头证明(1953年在前往国家物理实验室参加会议的火车车厢里), 但我不幸立刻忘记了细节. 这让我有一种不安的感觉, 认为证明一定很长或很复杂, 但实际上它如此简短和简单, 一般的读者可能也会感兴趣. 以下版本使用了CPL, 但并非本质性的.

假设T[R]是一个布尔函数, 它以没有形式或自由变量的例程(或程序)R作为参数, 并且对于所有R, 如果R运行时终止, 则T[R] = True; 如果R不终止, 则T[R] = False.

考虑如下定义的例程P:

rec routine P
§L: if T[P] go to L
Return §

如果T[P] = True, 例程P将进入循环, 只有T[P] = False时它才会终止. 在每种情况下,T[P]的值都恰好是错误的, 这个矛盾表明函数T不可能存在.

您诚挚的,
C. Strachey

丘吉尔学院, 剑桥

暂停一下

尝试停下来, 从上面的信中提取证明定理 9.3的论证.

由于CPL如今已不常见, 让我们复现这个证明. 思路如下: 为了推出矛盾, 假设存在一个程序T, 使得T(f,x)等于True当且仅当f在输入x上停机. (Strachey的信考虑的是 $HALT$ 的无输入变体, 但我们会看到, 这一区别并非本质上的)然后我们可以构造一个程序P和一个输入x, 使得T(P,x)给出错误的答案. 思路是, 在输入x上, 程序P将执行以下操作: 运行T(x,x), 如果答案是True, 则进入无限循环, 否则停机. 现在你可以看到T(P,P)会给出错误的答案: 如果P在以其自身代码作为输入时停机, 那么T(P,P)本应为True, 但P(P)将进入无限循环. 而如果P不停机, 那么T(P,P)本应为False, 但P(P)却会停机. 我们也可以用Python编写这段代码:

def CantSolveMe(T):
    """
    接受一个声称能解决停机问题的函数T. 
    返回一个由代码和输入组成的二元组(P,x)使
    T(P,x) ≠ HALT(x)
    """
    def fool(x):
        if T(x,x):
            while True: pass
        return "我停机了"

    return (fool,fool)

例如, 考虑以下天真的Python程序T, 它猜测一个给定的函数如果其输入包含while或for就不会停机:

def T(f,x):
    """粗略的停机测试器——如果程序含包含循环, 则判定其不停机"""
    import inspect
    source = inspect.getsource(f)
    if source.find("while"): return False
    if source.find("for"): return False
    return True

如果我们现在设置(f,x) = CantSolveMe(T), 那么T(f,x)=False, 但f(x)实际上却停机了. 这当然不是这个特定T独有的问题: 对于每个程序T, 如果我们运行(f,x) = CantSolveMe(T), 我们都会得到一个输入, 在该输入上T对 $HALT$ 给出了错误的答案.

9.4 归约

停机问题被证明是不可计算性的关键, 因为定理 9.3已被用来证明大量有趣函数的不可计算性. 我们将在本章和练习中看到几个这样的结果示例, 但还有更多此类结果(见图 9.6).

haltreductions-fig

图 9.6. 一些不可计算性结果. 从问题X指向问题Y的箭头表示我们通过将计算X归约为计算Y, 利用X的不可计算性来证明Y的不可计算性. 除MRDP定理外, 所有这些结果都出现在正文或练习中. 停机问题 $HALT$ 是我们所有这些不可计算性结果以及许多其他结果的起点.

这类不可计算性结果背后的思路在概念上很简单, 但起初可能相当令人困惑. 如果我们知道 $HALT$ 是不可计算的, 并且我们想证明某个其他函数 $BLAH$ 是不可计算的, 那么我们可以通过逆否论证(即反证法)来实现. 也就是说, 我们证明如果存在一个计算 $BLAH$ 的图灵机, 那么就存在一个计算 $HALT$ 的图灵机. (实际上, 这正是我们证明 $HALT$ 本身不可计算的方式, 即从定理 9.2的函数 $F^{*}$ 的不可计算性推导出这一事实)

例如, 为了证明 $BLAH$ 是不可计算的, 我们可以证明存在一个可计算函数 $R : {0, 1}^{*} \to {0, 1}^{*},$ 使得对于每对 $M$ 和 $x,$ 都有 $HALT (M, x) = BLAH (R (M, x)) .$ 存在这样一个函数 $R$ 意味着, 如果 $B L A H$ 是可计算的, 那么 $HALT$ 也将是可计算的, 从而导致矛盾! 关于归约令人困惑的部分在于, 我们假设一些我们相信为假的东西(即 $BLAH$ 有算法), 以推导出一些我们知道为假的东西(即 $HALT$ 有算法). Michael Sipser将这类结果描述为具有 “如果猪能吹口哨, 那么马就能飞” 的形式.

基于归约的证明有两个组成部分. 首先, 由于我们需要 $R$ 是可计算的, 我们应该描述计算它的算法. 计算 $R$ 的算法被称为归约, 因为变换 $R$ 将 $HALT$ 的输入修改为 $BLAH$ 的输入, 从而将计算 $HALT$ 的任务归约为计算 $BLAH$ 的任务. 基于归约的证明的第二个组成部分是对算法 $R$ 的分析: 即证明 $R$ 确实满足所需的性质.

基于归约的证明与其他反证法类似, 但它们涉及那些并不真正存在的假设性算法, 这往往使得归约相当令人困惑. 唯一的一点慰藉是, 归根结底, 归约的概念在数学上非常简单, 因此, 即使你每次都需要回到基本原理来记住归约的方向, 也并不是那么糟糕.

Info

备注 9.3 (归约是算法). 归约是一个算法, 这意味着, 如备注0.3所讨论的, 一个归约有三个组成部分:

规范(做什么): 在从 $HALT$ 到 $BLAH$ 的归约中, 规范是函数 $R : {0, 1}^{*} \to {0, 1}^{*}$ 应满足对于每个图灵机 $M$ 和输入 $x,$ $HALT (M, x) = BLAH (R (M, x)) .$ 一般来说, 要将函数 $F$ 归约到 $G,$ 归约应满足对于 $F$ 的每个输入 $w,$ $F (w) = G (R (w)) .$
实现(怎么做): 算法的描述: 将输入 $w$ 转换为输出 $y = R (w)$ 的精确指令.
分析(为什么): 证明算法符合规范的证明. 特别地, 在从 $F$ 到 $G$ 的归约中, 这是证明对于每个输入 $w,$ 算法的输出 $y = R (w)$ 满足 $F (w) = G (y) .$

9.4.1 示例: 零输入停机问题

这里有一个通过归约进行证明的具体例子. 我们定义函数 $HALTONZERO : {0, 1}^{*} \to {0, 1}$ 如下: 给定任意字符串 $M,$ $HALTONZERO (M) = 1$ 当且仅当 $M$ 描述了一个在给定字符串 $0$ 作为输入时会停机的图灵机. 先验地, $HALTONZERO$ 似乎比完整的 $HALT$ 函数可能更容易计算, 因此我们或许可以希望它是可计算的. 然而, 下面的定理表明情况并非如此:

定理 9.4 (无输入停机问题).

$HALTONZERO$ 是不可计算的.

暂停一下

定理 9.4的证明在下方, 但在阅读之前, 你可能需要暂停几分钟, 思考您自己将如何证明它. 特别是, 尝试思考从 $HALT$ 到 $HALTONZERO$ 的归约会是什么样子. 这样做是初步熟悉归约证明概念的绝佳方式, 这是我们将在本书中反复使用的一种技术. 你也可以查看图 9.8和随附的Colab笔记本, 了解此归约的Python实现.

haltonzerofig

图 9.7. 为了证明定理 9.4, 我们通过给出从计算 $HALT$ 的任务到计算 $HALTONZERO$ 的任务的归约, 来证明 $HALTONZERO$ 是不可计算的. 这表明如果存在一个假设计算 $HALTONZERO$ 的算法 $A,$ 那么就会存在一个计算 $HALT$ 的算法 $B,$ 这与定理 9.3矛盾. 由于 $A$ 和 $B$ 实际上都不存在, 这是一个“如果猪能吹口哨, 那么马就能飞“形式的蕴含示例.

定理 9.4的证明

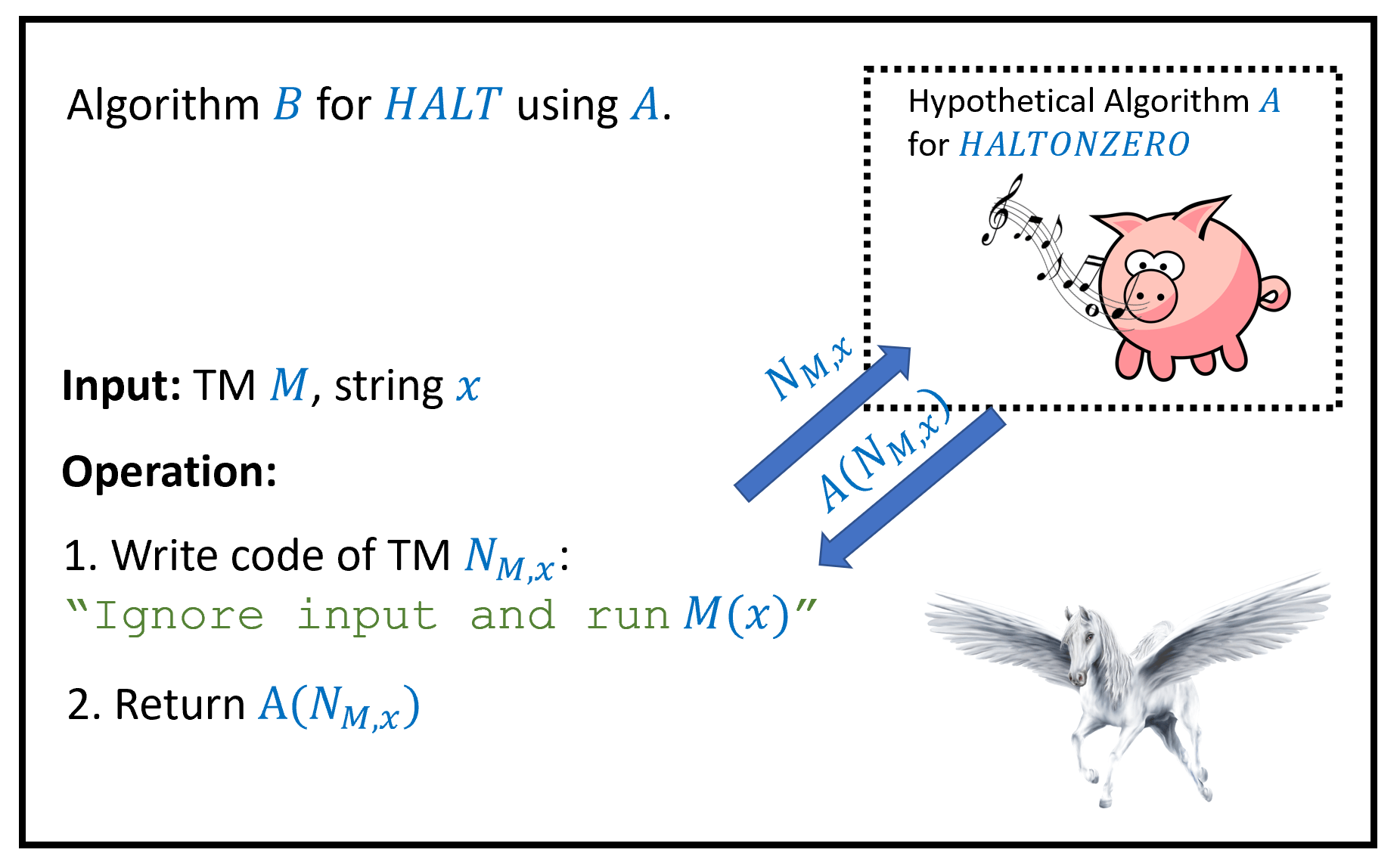
该证明通过从 $HALT$ 归约来完成, 参见图 9.7. 为了推出矛盾, 我们假设 $HALTONZERO$ 可由某个算法 $A$ 计算, 并利用这个假想的算法 $A$ 来构造一个计算 $HALT$ 的算法 $B,$ 从而得到与定理 9.3的矛盾. (如重要启示10中所讨论的, 遵循我们“鱼与熊掌兼得“的范式, 我们只使用通用名称“算法“, 而不关心是将它们建模为图灵机, NAND-TM程序, NAND-RAM等; 这没有区别, 因为所有这些模型都是彼此等价的)

由于这是我们第一次从停机问题出发进行归约证明, 我们将比往常更详细地阐述它. 这样的归约证明包括两个步骤:

归约描述: 我们将描述我们的算法 $B$ 的操作, 以及它如何对假想的算法 $A$ 进行“函数调用“.
归约分析: 然后我们将证明, 在算法 $A$ 计算 $HALTONZERO$ 的假设下, 算法 $B$ 将计算 $HALT .$

我们的算法 $B$ 工作如下: 在输入 $M, x$ 上, 它运行算法 9.1以获得一个图灵机 $M^{'},$ 然后返回 $A (M^{'}) .$ 机器 $M^{'}$ 忽略其输入 $z,$ 只运行 $M$ 于 $x$ 上.

在伪代码中, 程序 $N_{M, x}$ 看起来大致如下:

def N(z):
    M = r'.......'  # 包含 M 描述的字符串常量
    x = r'.......'  # 包含 x 的字符串常量
    return eval(M,x) # 注意我们忽略了输入 z

也就是说, 如果我们将 $N_{M, x}$ 视为一个程序, 那么它是一个包含 $M$ 和 $x$ 作为“硬编码常量“的程序, 给定任何输入 $z,$ 它 simply 忽略输入并总是返回在 $x$ 上运行 $M$ 的结果. 算法 $B$ 并不实际执行机器 $N_{M, x} .$ $B$ 仅仅将 $N_{M, x}$ 的描述作为字符串写下(就像我们上面做的那样), 并将这个字符串作为输入提供给 $A .$

以上完成了归约的描述. 分析通过证明以下断言获得:

断言: 对于每个字符串 $M, x, z,$ 由算法 $B$ 在步骤1中构造的机器 $N_{M, x}$ 满足: $N_{M, x}$ 在 $z$ 上停机当且仅当由 $M$ 描述的程序在输入 $x$ 上停机.

断言证明: 由于 $N_{M, x}$ 忽略其输入并使用通用图灵机在 $x$ 上评估 $M,$ 它在 $z$ 上停机当且仅当 $M$ 在 $x$ 上停机.

特别地, 如果我们用输入 $z = 0$ 来实例化这个断言, 我们看到 $HALTONZERO (N_{M, x}) = H A L T (M, x) .$ 因此, 如果假想的算法 $A$ 对每个 $M$ 满足 $A (M) = HALTONZERO (M),$ 那么我们构造的算法 $B$ 对每个 $M, x$ 满足 $B (M, x) = H A L T (M, x),$ 这与 $H A L T$ 的不可计算性相矛盾.

haltonzeropythonfig

图 9.8. 一个Python实现, 展示了如果 $HALT$ 不可计算, 则 $HALTONZERO$ 也不可计算的归约. 有关此归约的完整实现, 请参见此Colab笔记本.

算法 9.2 ( $HALT$ 到 $HALTONZERO$ 的归约).

$Input : 图灵机 M 和字符串 x Output : 图灵机 M^{'} 使得 M 在输入 x 上停机当且仅当 M^{'} 在输入 0 时停机 procedure N_{M, x} (w) # 图灵机 N_{M, x} 的描述 return EVAL (M, x) # 忽略输入, 并在 x 上运行 M endproc return N_{M, x} # 我们并不运行 N_{M, x}, 只返回其描述$

Info

备注 9.4 (硬编码技术).

在定理 9.4的证明中, 我们使用了将输入 $x$ “硬编码“到程序/机器 $P$ 中的技术. 也就是说, 我们取一个计算函数 $x \mapsto f (x)$ 的程序, 并将一些输入“固定“或“硬编码“为某个常数值. 例如, 如果你有一个程序, 它接受一对数字 $x, y$ 作为输入并输出它们的乘积(即计算函数 $f (x, y) = x \times y),$ 那么你可以将第二个输入“硬编码“为 $17,$ 从而获得一个程序, 它接受一个数字 $x$ 作为输入并输出 $x \times 17$ (即计算函数 $g (x) = x \times 17) .$ 这种技术在归约证明和其他地方非常常见, 我们将在本书中反复使用它.

9.5 Rice定理与通用软件验证的不可能性

停机问题的不可计算性其实是一个更普遍现象的特殊情况. 即, 我们无法证明通用程序的语义属性. “语义属性“指的是程序计算的函数的属性, 而不是依赖于程序使用的特定语法的属性.

程序 $P$ 的语义属性的一个例子是: 只要 $P$ 被给定一个具有偶数个 $1$ 的输入字符串, 它就输出 $0.$ 另一个例子是: 当输入以 $1$ 结尾时, $P$ 将始终停机. 相比之下, C程序在每个函数声明之前包含注释的属性不是语义属性, 因为它依赖于实际的源代码, 而不是输入/输出关系.

检查程序的语义属性非常重要, 因为它对应于检查程序是否符合规范. 但结果证明这样的属性通常是不可计算的. 我们已经看到了一些不可计算语义函数的例子, 即 $HALT$ 和 $HALTONZERO,$ 但这些只是“冰山一角“. 我们首先观察另一个这样的例子:

定理 9.5 (计算全零函数).

设 $ZEROFUNC : {0, 1}^{*} \to {0, 1}$ 为如下函数: 对于每个 $M \in {0, 1}^{*},$ $ZEROFUNC (M) = 1$ 当且仅当 $M$ 表示一个图灵机, 且该图灵机在每个输入 $x \in {0, 1}^{*}$ 上都输出 $0.$ 那么 $ZEROFUNC$ 是不可计算的.

暂停一下

尽管名称相似, $ZEROFUNC$ 和 $HALTONZERO$ 是两个不同的函数. 例如, 如果 $M$ 是一个图灵机, 在输入 $x \in {0, 1}^{*}$ 上, 停机并输出 $x$ 的所有坐标的与, 那么 $HALTONZERO (M) = 1$ (因为 $M$ 在输入 $0$ 上确实停机), 但 $ZEROFUNC (M) = 0$ (因为 $M$ 不计算常数零函数).

定理 9.5的证明

证明通过从 $HALTONZERO$ 归约来完成. 为了推出矛盾, 假设存在一个算法 $A,$ 使得对每个 $M \in {0, 1}^{*},$ $A (M) = ZEROFUNC (M) .$ 那么我们将构造一个算法 $B$ 来解决 $HALTONZERO,$ 从而与定理 9.4矛盾.

给定一个图灵机 $N$ (它是 $HALTONZERO$ 的输入), 我们的算法 $B$ 执行以下操作:

构造一个图灵机 $M,$ 它在输入 $x \in {0, 1}^{*}$ 上, 首先运行 $N (0),$ 然后输出 $0.$
返回 $A (M) .$

现在, 如果 $N$ 在输入 $0$ 上停机, 那么图灵机 $M$ 计算常数零函数, 因此在我们假设 $A$ 计算 $ZEROFUNC$ 的情况下, $A (M) = 1.$ 如果 $N$ 在输入 $0$ 上不停机, 那么图灵机 $M$ 在任何输入上都不会停机, 因此特别地, 它不计算常数零函数. 因此在我们假设 $A$ 计算 $ZEROFUNC$ 的情况下, $A (M) = 0.$ 我们看到在两种情况下, $ZEROFUNC (M) = HALTONZERO (N),$ 因此算法 $B$ 在步骤 2 返回的值等于 $HALTONZERO (N),$ 这正是我们需要证明的.

另一个类似的结果如下:

定理 9.6 (验证奇偶性的不可计算性).

以下函数是不可计算的: $COMP U TES - P A R I T Y (P) = {10 P 计算奇偶函数否则$

暂停一下

我们将定理 9.6的证明留作练习(习题 9.6). 我强烈建议你停在这里, 尝试解决这个练习.

9.5.1 Rice定理

定理 9.6可以推广到远不止奇偶校验函数. 事实上, 这种推广排除了对程序进行任何类型的语义规约验证的可能性. 我们将程序上的一个语义规约(semantic specification)定义为某种不依赖于程序代码, 而只依赖于程序所计算的函数的性质.

例如, 考虑以下两个C程序:

int First(int n) {
    if (n<0) return 0;
    return 2*n;
}

int Second(int n) {
    int i = 0;
    int j = 0
    if (n<0) return 0;
    while (j<n) {
        i = i + 2;
        j = j + 1;
    }
    return i;
}

First和Second是两个不同的C程序, 但它们计算相同的函数. 一个语义性质, 对这两个程序要么同时为真, 要么同时为假, 因为它依赖于程序计算的函数, 而不是它们的代码. First和Second都满足的一个语义性质的例子是: “程序 $P$ 计算一个将整数映射到整数的函数 $f,$ 满足对于每个输入 $n,$ $f (n) \geq n$ ”.

如果一个性质依赖于源代码本身而不是输入/输出行为, 那么它就是非语义的. 例如, “程序包含变量k” 或 “程序使用了while操作” 等性质就不是语义的. 这样的性质可能对一个程序为真, 而对其他程序为假.

形式化地, 我们定义语义性质如下:

定义 9.2 (语义性质).

如果对于每个 $x \in {0, 1}^{*},$ 都有 $M (x) = M^{'} (x),$ 则称一对图灵机 $M$ 和 $M^{'}$ 是功能等价的(functionally equivalent). (特别地, 对于所有 $x,$ $M (x) = ⊥$ 当且仅当 $M^{'} (x) = ⊥)$

一个函数 $F : {0, 1}^{*} \to {0, 1}$ 是语义的, 如果对于每一对表示功能等价图灵机的字符串 $M, M^{'},$ 都有 $F (M) = F (M^{'}) .$ (回想一下, 我们假设每个字符串都表示某个图灵机, 参见备注 9.1)

语义函数有两个平凡的例子: 常值1函数和常值0函数. 例如, 如果 $Z$ 是常零函数(即, 对于每个 $M,$ $Z (M) = 0),$ 那么显然对于每一对功能等价的图灵机 $M$ 和 $M^{'},$ 都有 $F (M) = F (M^{'}) .$ 下面是一个非平凡的例子:

Question

练习 9.1 ( $ZEROFUNC$ 是语义的).

证明函数 $ZEROFUNC$ 是语义的.

对练习 9.1的解答

回想一下, $ZEROFUNC (M) = 1$ 当且仅当对于每个 $x \in {0, 1}^{*},$ $M (x) = 0.$ 如果 $M$ 和 $M^{'}$ 功能等价, 那么对于每个 $x,$ $M (x) = M^{'} (x) .$ 因此, $ZEROFUNC (M) = 1$ 当且仅当 $ZEROFUNC (M^{'}) = 1.$

通常, 我们最感兴趣计算的程序性质是语义的, 因为我们希望理解程序的功能. 不幸的是, Rice定理告诉我们这些性质都是不可计算的:

定理 9.7 (Rice定理).

设 $F : {0, 1}^{*} \to {0, 1} .$ 如果 $F$ 是语义的且非平凡的, 那么它是不可计算的.

定理 9.7的证明思路

证明背后的思路是表明, 每个语义的非平凡函数 $F$ 至少和计算 $HALTONZERO$ 一样困难. 这将完成证明, 因为根据定理 9.4, $HALTONZERO$ 是不可计算的. 如果一个函数 $F$ 是非平凡的, 那么存在两个机器 $M_{0}$ 和 $M_{1},$ 使得 $F (M_{0}) = 0$ 且 $F (M_{1}) = 1.$ 因此, 目标是取一个机器 $N,$ 并设法将其映射到一个机器 $M = R (N),$ 使得**(i)**如果 $N$ 在输入0上停机, 则 $M$ 功能等价于 $M_{1};$ (ii) 如果 $N$ 在输入0上不停机, 则 $M$ 功能等价于 $M_{0} .$

因为 $F$ 是语义的, 如果我们实现了这一点, 那么我们将保证 $HALTONZERO (N) = F (R (N)),$ 从而表明如果 $F$ 是可计算的, 那么 $HALTONZERO$ 也将是可计算的, 这与定理 9.4矛盾.

定理 9.7的证明

我们不会给出完全形式化的证明, 而是通过将注意力限制在一个特定的语义函数 $F$ 上来阐述证明思路. 然而, 同样的技术可以推广到所有可能的语义函数. 定义 $MONOTONE : {0, 1}^{*} \to {0, 1}$ 如下: $MONOTONE (M) = 1,$ 如果不存在 $n \in N$ 和两个输入 $x, x^{'} \in {0, 1}^{n},$ 使得对于每个 $i \in [n],$ $x_{i} \leq x_{i}^{'},$ 但 $M (x)$ 输出 $1$ 且 $M (x^{'}) = 0.$ 也就是说, $MONOTONE (M) = 1$ 如果不可能找到一个输入 $x,$ 使得将 $x$ 的某些位从0翻转为1会将 $M$ 的输出从1反方向改变为0. 我们将证明 $MONOTONE$ 是不可计算的, 但该证明很容易推广到任何语义函数.

我们首先注意到 $MONOTONE$ 既不是常值零函数, 也不是常值一函数:

在所有输入上直接进入无限循环的机器 $INF$ 满足 $MONOTONE (INF) = 1,$ 因为 $INF$ 在任何地方都没有定义, 因此特别地, 不存在两个输入 $x, x^{'},$ 使得对于每个 $i$ 有 $x_{i} \leq x_{i}^{'},$ 但 $INF (x) = 0$ 且 $INF (x^{'}) = 1.$
计算其输入的 $XOR$ 或奇偶性(异或)的机器 $PAR$ 不是单调的(例如, $PAR (1, 1, 0, 0, \dots, 0) = 0$ 但 $PAR (1, 0, 0, \dots, 0) = 0),$ 因此 $MONOTONE (PAR) = 0.$

(注意 $INF$ 和 $PAR$ 是机器而不是函数)

现在, 我们将给出一个从 $HALTONZERO$ 到 $MONOTONE$ 的归约. 也就是说, 我们假设存在一个计算 $MONOTONE$ 的算法 $A,$ 并由此导出矛盾, 然后我们将构建一个计算 $HALTONZERO$ 的算法 $B .$ 我们的算法 $B$ 将如下工作:

算法 $B :$
输入: 描述图灵机的字符串 $N .$ (目标: 计算 $HALTONZERO (N))$
假设: 可以访问计算 $MONOTONE$ 的算法 $A .$
操作:
- 构造以下机器 $M :$ “对于输入 $z \in {0, 1}^{*},$ 执行: (a) 运行 $N (0),$ (b) 返回 $PAR (z)$ ”.
- 返回 $1 - A (M) .$

为了完成证明, 我们需要证明, 在我们假设 $A$ 计算 $MONOTONE$ 的前提下, $B$ 输出了正确答案. 换句话说, 我们需要证明 $HALTONZERO (N) = 1 - MONOTONE (M) .$ 假设 $N$ 在输入 0 上不停机. 在这种情况下, 算法 $B$ 构造的程序 $M$ 在步骤 (a) 进入无限循环, 并且永远不会到达步骤 (b). 因此, 在这种情况下, $N$ 功能等价于 $INF .$ (机器 $N$ 与 $INF$ 不是同一个机器: 它的描述或代码不同. 但它的输入/输出行为(在这种情况下)确实相同, 即在任何输入上都不停机. 另外, 虽然程序 $M$ 将在每个输入上进入无限循环, 但算法 $B$ 从未实际运行 $M :$ 它只生成其代码并将其提供给 $A .$ 因此, 即使在这种情况下, 算法 $B$ 也不会进入无限循环)所以在这种情况下, $MONOTONE (M) = MONOTONE (INF) = 1.$

如果 $N$ 在输入0上确实停机, 那么 $M$ 中的步骤**(a)** 最终将结束, 并且 $M$ 的输出将由步骤**(b)** 决定, 即它简单地输出其输入的奇偶性. 因此, 在这种情况下, $M$ 计算的是非单调的奇偶性函数(即功能等价于 $PAR),$ 所以我们得到 $MONOTONE (M) = MONOTONE (PAR) = 0.$ 在这两种情况下, $MONOTONE (M) = 1 - H A L TONZERO (N),$ 这正是我们想要证明的.

检查这个证明可以发现, 除了 $MONOTONE$ 是语义且非平凡的之外, 我们没有使用关于它的任何其他信息. 对于每个语义的非平凡函数 $F,$ 我们可以使用相同的证明, 只需将 $PAR$ 和 $INF$ 替换为两个机器 $M_{0}$ 和 $M_{1},$ 使得 $F (M_{0}) = 0$ 且 $F (M_{1}) = 1.$ 如果 $F$ 是非平凡的, 这样的机器必须存在.

Info

备注 9.5 (语义性不等于不可计算性).

Rice定理非常强大, 并且是证明不可计算性的一种流行方法, 以至于人们有时会感到困惑, 认为它是证明不可计算性的唯一方法. 特别地, 一个常见的误解是, 如果一个函数 $F$ 不是语义的, 那么它就是可计算的. 这完全不是事实.

例如, 考虑以下函数 $HALTNOYALE : {0, 1}^{*} \to {0, 1} .$ 这个函数在输入一个表示NAND-TM程序 $P$ 的字符串时, 输出 $1$ 当且仅当 (i) $P$ 在输入 $0$ 上停机, 并且 (ii) 程序 $P$ 不包含标识符为Yale的变量. 函数 $HALTNOYALE$ 显然不是语义的, 因为当输入以下两个功能等价程序之一时, 它将输出两个不同的值:

Yale[0] = NAND(X[0],X[0])
Y[0] = NAND(X[0],Yale[0])

Harvard[0] = NAND(X[0],X[0])
Y[0] = NAND(X[0],Harvard[0])

然而, $HALTNOYALE$ 是不可计算的, 因为每个程序 $P$ 都可以被转换成一个等价的(实际上是更好的:)) 程序 $P^{'},$ 该程序不包含变量Yale. 因此, 如果我们能计算 $HALTNOYALE,$ 那么我们就能判定NAND-TM程序(从而也能判定图灵机)在输入0上是否停机.

此外, 正如我们将在第11章中看到的, 存在一些不可计算函数, 其输入不是程序, 因此形容词“语义的“并不适用.

诸如“程序包含变量Yale“之类的性质有时被称为语法性质. “语义的“和“语法的“这两个术语的使用超出了编程语言的范围: 英语中一个著名的语法正确但语义无意义的句子是乔姆斯基的“Colorless green ideas sleep furiously.”(无色的绿色思想愤怒地睡觉)然而, 形式化定义“语法性质“相当微妙, 本书将不使用这个术语, 只使用“语义的“和“非语义的“这两个术语.

9.5.2 其他图灵完备模型的停机问题与Rice定理

正如我们之前所见, 许多自然计算模型被证明是彼此等价的, 因为我们可以将一个模型的“程序“(例如 $λ$ 表达式, 或生命游戏的格局)转换成另一个模型(例如NAND-TM程序). 这种等价性意味着, 我们可以将NAND-TM程序的停机问题的不可计算性转化为其他模型中停机问题的不可计算性. 例如:

定理 9.8 (NAND-TM机器停机问题).

设 $NANDTMHALT : {0, 1}^{*} \to {0, 1}$ 为函数, 对于输入字符串 $P \in {0, 1}^{*}$ 和 $x \in {0, 1}^{*},$ 如果由 $P$ 描述的NAND-TM程序在输入 $x$ 上停机, 则输出 $1,$ 否则输出 $0.$ 那么 $NANDTMHALT$ 是不可计算的.

暂停一下

再次强调, 这是你停下来尝试自己证明结果的好时机, 然后再阅读下面的证明.

定理 9.8的证明

我们在定理7.11中已经看到, 对于每个图灵机 $M,$ 都存在一个等价的NAND-TM程序 $P_{M},$ 使得对于每个 $x,$ $P_{M} (x) = M (x) .$ 特别地, 这意味着 $H A L T (M) = NANDTMHALT (P_{M}) .$

从定理7.11的证明中获得的变换 $M \mapsto P_{M}$ 是构造性的(constructive). 也就是说, 该证明提供了一种计算映射 $M \mapsto P_{M}$ 的方法. 这意味着该证明产生了一个从计算 $H A L T$ 的任务到计算 $NANDTMHALT$ 的任务的归约, 由于 $H A L T$ 是不可计算的, 所以 $NANDTMHALT$ 也是不可计算的.

同样的证明也适用于其他计算模型, 如 $λ$ 演算, 二维(甚至一维)自动机等. 因此, 例如, 没有算法可以判定一个 $λ$ 表达式是否计算恒等函数, 也没有算法可以判定生命游戏的初始格局最终是否会将单元格 $(0, 0)$ 染成黑色.

事实上, 我们可以将Rice定理推广到所有这些模型. 例如, 如果 $F : {0, 1}^{*} \to {0, 1}$ 是一个非平凡函数, 使得对于每对功能等价的NAND-TM程序 $P, P^{'}$ 都有 $F (P) = F (P^{'}),$ 那么 $F$ 是不可计算的, 这对于NAND-RAM程序, $λ$ 表达式以及所有其他图灵完备模型(如定义8.5所定义)同样成立, 另见习题 9.12.

9.5.3 软件验证被摧毁了吗? (讨论)

程序正越来越多地用于关键任务, 无论是运行我们的银行系统, 驾驶飞机还是监控核反应堆. 如果我们甚至无法提供一个认证算法来证明一个程序正确计算了奇偶校验函数, 那么我们怎么能确信一个程序做了它应该做的事情呢？关键见解是, 虽然不可能认证一个通用程序符合规约, 但可以在最初编写程序时采用一种使其更容易认证的方式. 举个简单的例子, 如果你编写一个没有循环的程序, 那么你可以证明它会停机. 此外, 虽然可能无法认证一个任意程序计算了奇偶校验函数, 但完全可以编写一个特定的程序 $P,$ 我们可以从数学上证明 $P$ 计算了奇偶校验. 事实上, 编写程序或算法并提供其正确性证明, 正是我们在算法研究中一直在做的事情.

软件验证(software verification)领域关注的是验证给定程序是否满足某些条件. 这些条件可以是程序计算了某个函数, 永远不会写入危险的内存位置, 遵守某些不变量等等. 虽然验证这些任务的一般性问题可能是不可计算的, 但研究人员已经成功地对许多有趣的案例进行了验证, 特别是如果程序最初就是用一种使验证更容易的形式化方法或编程语言编写的. 尽管如此, 验证, 尤其是大型复杂程序的验证, 在实践中仍然是一项极具挑战性的任务, 并且已被形式化证明正确的程序数量仍然很少. 此外, 即使是提出要证明的正确定理(即规约)本身, 也常常是一项非常重要的任务.

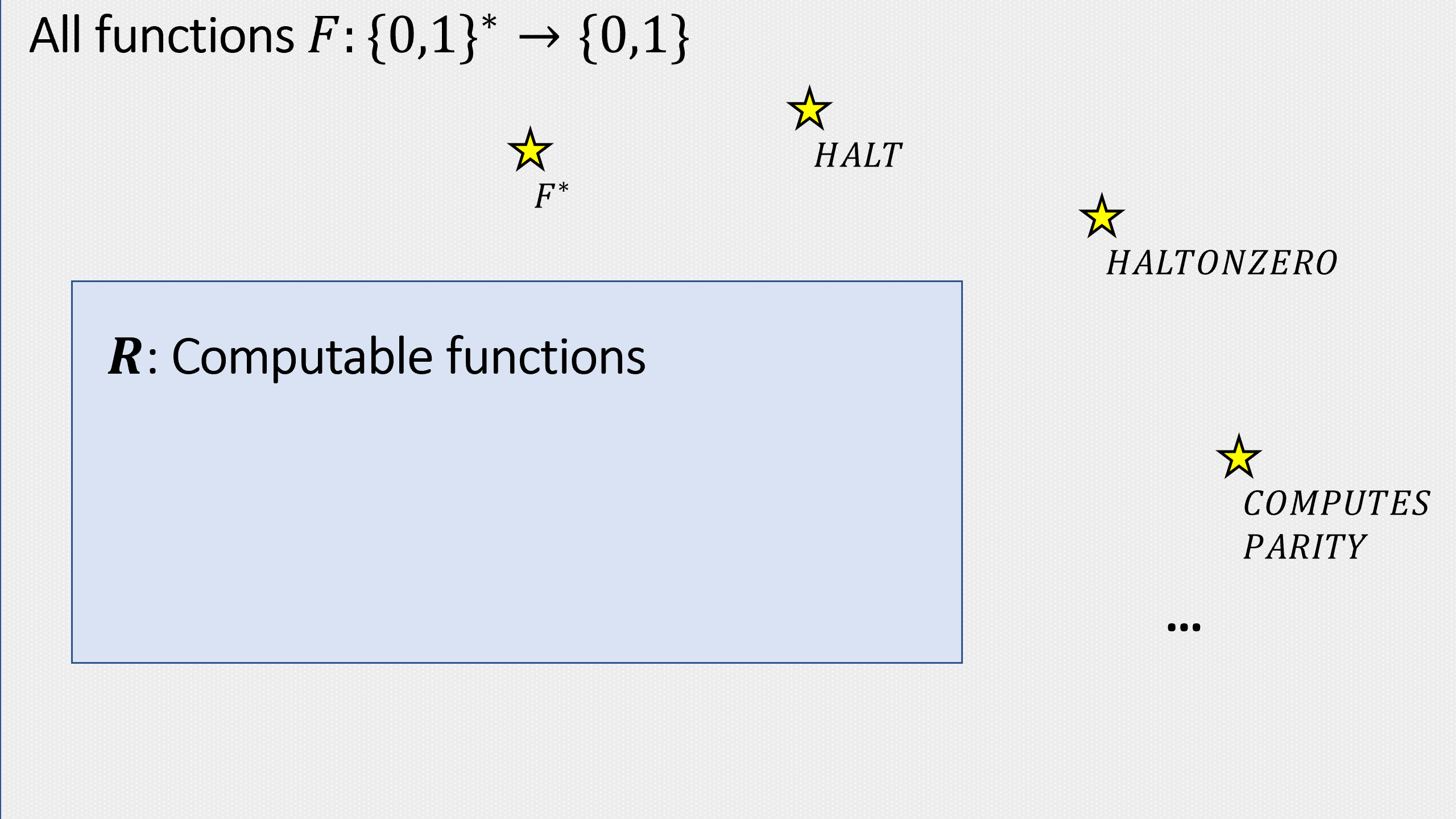
inclusionuncomputablefig

图 9.9. 可计算布尔函数集合 $R$ (定义7.3)是所有将 ${0, 1}^{*}$ 映射到 ${0, 1}$ 的函数集合的真子集. 在本章中, 我们看到了后者集合中一些不在前者集合中的元素的例子.

本章回顾

存在一个通用图灵机(或NAND-TM程序) $U,$ 使得在输入图灵机 $M$ 的描述和某个输入 $x$ 时, $U (M, x)$ 停机并输出 $M (x),$ 当(且仅当) $M$ 在输入 $x$ 上停机. 与有限计算(即NAND-CIRC程序/电路)的情况不同, 程序 $U$ 的输入可以是一个状态数比 $U$ 本身更多的机器 $M .$
与有限情况不同, 实际上存在一些本质上不可计算的函数, 即它们不能被任何图灵机计算.
这些不仅包括一些“退化“或“深奥“的函数, 还包括人们深切关注并曾猜想可以计算的函数.
如果Church-Turing论题成立, 那么根据我们的定义不可计算的函数 $F,$ 在我们的物理世界中无法通过任何方式计算.

9.6 习题

习题 9.1 (NAND-RAM停机问题).

设函数 $NANDRAMHALT : {0, 1}^{*} \to {0, 1}$ 满足: 对于输入 $(P, x),$ 其中 $P$ 表示一个NAND-RAM程序, $NANDRAMHALT (P, x) = 1$ 当且仅当程序 $P$ 在输入 $x$ 上停机. 证明 $NANDRAMHALT$ 是不可计算的.

习题 9.2 (时限停机问题).

设函数 $TIMEDHALT : {0, 1}^{*} \to {0, 1}$ 满足: 对于输入(表示三元组 $(M, x, T)$ 的)字符串, $TIMEDHALT (M, x, T) = 1$ 当且仅当图灵机 $M$ 在输入 $x$ 上至多在 $T$ 步内停机(其中一步定义为从纸带读取符号, 更新状态, 写入新符号以及(可能)移动读写头的一个完整操作序列). 证明 $TIMEDHALT$ 是可计算的.

习题 9.3 (空间停机问题(挑战)).

设函数 $SPACEHALT : {0, 1}^{*} \to {0, 1}$ 满足: 对于输入(表示三元组 $(M, x, T)$ 的)字符串, $SPACEHALT (M, x, T) = 1$ 当且仅当图灵机 $M$ 在输入 $x$ 上, 在其读写头到达其纸带的第 $T$ 个位置之前停机. (我们不关心 $M$ 执行了多少步, 只要读写头始终保持在位置 ${0, \dots, T - 1}$ 内即可)证明 $SPACEHALT$ 是可计算的. 提示见脚注²

习题 9.4 (可计算函数的组合).

假设 $F : {0, 1}^{*} \to {0, 1}$ 和 $G : {0, 1}^{*} \to {0, 1}$ 是可计算函数. 对于下列每个函数 $H,$ 要么证明 $H$ 必定是可计算的, 要么给出一对可计算函数 $F$ 和 $G$ 使得 $H$ 不可计算. 证明你的论断.

$H (x) = 1$ 当且仅当 $F (x) = 1$ 或 $G (x) = 1.$
$H (x) = 1$ 当且仅当存在两个非空字符串 $u, v \in {0, 1}^{*}$ 使得 $x = uv$ (即 $x$ 是 $u$ 和 $v$ 的连接), 并且 $F (u) = 1$ 且 $G (v) = 1.$
$H (x) = 1$ 当且仅当存在一个非空字符串的列表 $u_{0}, \dots, u_{t - 1},$ 使得对每个 $i \in [t]$ 都有 $F (u_{i}) = 1$ 且 $x = u_{0} u_{1} \dots u_{t - 1} .$
$H (x) = 1$ 当且仅当 $x$ 是NAND++程序 $P$ 的一个有效字符串表示, 并且满足对于每个 $z \in {0, 1}^{*},$ 程序 $P$ 在输入 $z$ 上的输出都是 $F (z) .$
$H (x) = 1$ 当且仅当 $x$ 是NAND++程序 $P$ 的一个有效字符串表示, 并且程序 $P$ 在输入 $x$ 上输出 $F (x) .$
$H (x) = 1$ 当且仅当 $x$ 是NAND++程序 $P$ 的一个有效字符串表示, 并且程序 $P$ 在输入 $x$ 上执行至多 $100 \cdot ∣ x ∣^{2}$ 行后输出 $F (x) .$

习题 9.5.

证明下列函数 $FINITE : {0, 1}^{*} \to {0, 1}$ 是不可计算的. 对于输入 $P \in {0, 1}^{*},$ 我们定义 $FINITE (P) = 1$ 当且仅当 $P$ 是一个表示NAND++程序的字符串, 并且只有有限个输入 $x \in {0, 1}^{*}$ 满足 $P (x) = 1.$ ³

习题 9.6 (计算奇偶性).

不使用Rice定理证明定理 9.6.

习题 9.7 (图灵机等价性).

定义函数 $EQ : {0, 1}^{*} :\to {0, 1}$ 如下: 给定一个表示图灵机对 $(M, M^{'})$ 的字符串, $EQ (M, M^{'}) = 1$ 当且仅当 $M$ 和 $M^{'}$ 根据定义 9.2是功能等价的. 证明 $EQ$ 是不可计算的.

注意, 你不能直接使用Rice定理, 因为该定理只处理以单个图灵机作为输入的函数, 而 $EQ$ 接收两个机器作为输入.

习题 9.8.

对于以下两个函数, 分别说明它们是否可计算:

给定一个NAND-TM程序 $P,$ 一个输入 $x$ 和一个数 $k,$ 当我们运行 $P$ 于 $x$ 时, 索引变量i是否曾达到 $k$ ?
给定一个NAND-TM程序 $P,$ 一个输入 $x$ 和一个数 $k,$ 当我们运行 $P$ 于 $x$ 时, $P$ 是否曾对数组索引 $k$ 的位置进行写操作?

习题 9.9.

设 $F : {0, 1}^{*} \to {0, 1}$ 为如下定义的函数. 对于输入一个表示NAND-RAM程序的字符串 $P$ 和一个表示图灵机的字符串 $M,$ $F (P, M) = 1$ 当且仅当存在某个输入 $x$ 使得 $P$ 在 $x$ 上停机而 $M$ 在 $x$ 上不停机. 证明 $F$ 是不可计算的. 提示见脚注. ⁴

习题 9.10 (递归可枚举性).

定义一个函数 $F : {0, 1}^{*} :\to {0, 1}$ 是递归可枚举的, 如果存在一台图灵机 $M$ 满足: 对于每个 $x \in {0, 1}^{*},$ 如果 $F (x) = 1$ 则 $M (x) = 1$ ；如果 $F (x) = 0$ 则 $M (x) = ⊥.$ (即, 如果 $F (x) = 0$ 则 $M$ 在 $x$ 上不停机)

证明每个可计算的 $F$ 也是递归可枚举的.
证明存在一个函数 $F,$ 它不是可计算的, 但是递归可枚举的. 提示见脚注. ⁵
证明存在一个函数 $F : {0, 1}^{*} \to {0, 1},$ 它不是递归可枚举的. 提示见脚注. ⁶
证明存在一个函数 $F : {0, 1}^{*} \to {0, 1},$ 它是递归可枚举的, 但由 $\overline{F} (x) = 1 - F (x)$ 定义的函数 $\overline{F}$ 不是递归可枚举的. 提示见脚注. ⁷

习题 9.11 (Rice定理: 标准形式).

在本练习中, 我们将证明文献中通常形式的Rice定理.

对于一台图灵机 $M,$ 定义 $L (M) \subseteq {0, 1}^{*}$ 为所有满足 $M$ 在输入 $x$ 上停机并输出 $1$ 的 $x \in {0, 1}^{*}$ 的集合. (集合 $L (M)$ 在文献中称为由 $M$ 识别的语言. 注意, 对于不在 $L (M)$ 中的输入 $x,$ $M$ 可能输出非 $1$ 的值或者根本不停机)

证明对于每台图灵机 $M,$ 如果我们定义函数 $F_{M} : {0, 1}^{*} \to {0, 1}$ 满足 $F_{M} (x) = 1$ 当且仅当 $x \in L (M),$ 那么 $F_{M}$ 是如习题 9.10所定义的递归可枚举函数.
使用定理 9.7证明, 对于每个函数 $G : {0, 1}^{*} \to {0, 1},$ 如果 (a) $G$ 既不是恒等于 $0$ 也不是恒等于 $1$ 的函数, 并且 (b) 对于每对满足 $L (M) = L (M^{'})$ 的 $M, M^{'}$ 都有 $G (M) = G (M^{'}),$ 那么 $G$ 是不可计算的. 提示见脚注. ⁸

习题 9.12 (适用于通用图灵等价模型的Rice定理(可选)).

设 $F$ 为所有从 ${0, 1}^{*}$ 到 ${0, 1}$ 的部分函数的集合, $M : {0, 1}^{*} \to F$ 是定义8.5中定义的图灵等价模型. 我们称一个函数 $F : {0, 1}^{*} \to {0, 1}$ 是* $M$ -语义的*, 如果存在某个 $G : F \to {0, 1}$ 使得对于每个 $P \in {0, 1}^{*}$ 都有 $F (P) = G (M (P)) .$

证明对于每个既非常数 $1$ 也非常数 $0$ 的 $M$ -语义函数 $F : {0, 1}^{*} \to {0, 1},$ $F$ 是不可计算的.

习题 9.13 (忙碌海狸).

本题中我们定义忙碌海狸函数的NAND-TM变体(参见Aaronson于1999年的论文, 2017年的博客文章和2020年的综述(Aaronson, 2020); 另见Tao关于文明科学进步如何通过我们能理解的量来衡量的演讲).

定义 $T_{BB} : {0, 1}^{*} \to N$ 如下: 对于每个字符串 $P \in {0, 1}^{*},$ 如果 $P$ 表示一个NAND-TM程序, 并且当 $P$ 在输入 $0$ 上执行时在 $M$ 步内停机, 则 $T_{BB} (P) = M .$ 否则(如果 $P$ 不代表一个NAND-TM程序, 或者它是一个在 $0$ 上不停机的程序), $T_{BB} (P) = 0.$ 证明 $T_{BB}$ 是不可计算的.
令 $TO W ER (n)$ 表示数 $n 次 2^{\cdot^{\cdot^{\cdot^{2}}}}$ (即高度为 $n$ 的“二的幂塔”). 为了体会这个函数增长有多快, $TO W ER (1) = 2,$ $TO W ER (2) = 2^{2} = 4,$ $TO W ER (3) = 2^{2^{2}} = 16,$ $TO W ER (4) = 2^{16} = 65536,$ 而 $TO W ER (5) = 2^{65536}$ 大约是 $1 0^{20000} .$ $TO W ER (6)$ 已经是一个即使用科学记数法也难以书写的巨大数字. 定义 $NBB : N \to N$ (代表“NAND-TM Busy Beaver“)为函数 $NBB (n) = max_{P \in {0, 1}^{n}} T_{BB} (P),$ 其中 $T_{BB}$ 如问题6.1所定义. 证明 $NBB$ 的增长速度快于 $TO W ER,$ 即 $TO W ER (n) = o (NBB (n)) .$ 提示见脚注⁹

5.9 参考书目

图 9.1中关于停机问题的漫画取自Charles Cooper的网站, 版权归2019年Charles F. Cooper所有.

(Moore与Mertens, 2011年)第7.2节对不可计算性作了高度推荐的概述. 《Gödel, Escher, Bach》(Hofstadter, 1999年)是一本经典科普著作, 涉及不可计算性, 不可证明性, 特别是我们将在第11章看到的哥德尔定理. 亦可参考Holt的新书(Holt, 2018年).

函数定义的历史与数学作为一个领域的发展交织在一起. 多年以来, 函数被(依照上述Euler的表述)视为从输入计算输出的方法. 19世纪, 随着Fourier级数的发明以及对连续性和可微性的系统研究, 人们开始关注更一般的函数类型, 但将函数定义为任意映射的现代定义尚未被普遍接受. 例如, Poincare在1899年写道：*“我们见到大量奇异的函数, 它们似乎被迫尽可能不像那些有实际用途的正当函数…这些函数被特意构造出来, 只为证明我们先辈的推理存在缺陷, 除此之外我们从中得不到任何东西”*部分精彩的历史论述可参阅(Grabiner, 1983)(Kleiner, 1991)(Lützen, 2002)(Grabiner, 2005).

通用图灵机的存在以及 $HALT$ 的不可计算性最早由Turing在其开创性论文(Turing, 1937)中证明, 但Church在前一年已证明了密切相关的结论. 这些工作建立在Gödel1931年的不完备性定理基础上, 我们将在第11章讨论该定理.

(Rogozhin, 1996)给出了一些字母表和状态数较小的通用图灵机, 包括采用二进制字母表且状态数少于 $25$ 的单带通用图灵机；亦可参阅综述(Woods与Neary, 2009). Adam Yedidia开发了辅助生成较少状态灵机的软件. 这与“代码高尔夫”这种娱乐活动相关, 旨在用尽可能短的程序解决特定计算任务. 寻找“高度复杂“的小型图灵机也与“忙碌海狸“问题有关, 参见习题 9.13及综述(Aaronson, 2020).

用于证明 $F^{*}$ 不可计算性的对角线论证法源于第2章讨论的康托尔关于实数不可数的论证.

Christopher Strachey是英国计算机科学家, CPL编程语言的发明者. 他也是早期人工智能领域的先驱, 在1950年代初期就编程使计算机能下跳棋甚至写情书, 详见《纽约客》文章与此网站.

Rice定理在(Rice, 1953)中被证明. 其常见表述形式与我们所采用的略有不同, 参见习题 9.11.

本章未讨论递归可枚举语言的概念, 但习题 9.10简要涉及了该内容. 我们照例使用函数记法而非语言记法.

1: 这一论点也与意识和自由意志的问题相关. 我个人对其与这些问题的相关性持怀疑态度. 或许推理过程是: 人类有能力解决停机问题, 但他们通过选择不这样做来行使自由意志和意识.

2: 一台字母表为 $Σ$ 的机器, 其纸带前 $T$ 个位置的内容最多有 $∣Σ ∣^{T}$ 种可能. 如果机器重复了之前出现过的配置(即纸带内容, 读写头位置和当前状态都与之前某个执行状态完全相同), 会发生什么?

3: 提示: 你可以使用Rice定理.

4: 提示: 虽然不能直接应用, 但稍作“调整“后, 你可以使用Rice定理来证明这一点.

5: $HALT$ 具有此性质.

6: 你可以使用对角化方法直接证明, 或者证明所有递归可枚举函数的集合是可数的.

7: $HALT$ 具有此性质: 证明如果 $HALT$ 和 $\overline{HALT}$ 都是递归可枚举的, 那么 $HALT$ 实际上将是可计算的.

8: 证明任何满足 (b) 的 $G$ 都必须是语义的.

9: 在本练习中, 你不需要使用 $TO W ER$ 函数非常具体的性质. 例如, $NBB (n)$ 的增长也快于Ackerman函数.

| 理论计算机科学导论 |