❗页面施工中: 目前状态: 创建教程中.
要求:
- ✅将所有numthm环境用灰色admonish(quote)框起.
- ✅标点符号统一为英文.
- ✅使用添加对文内特定位置的超链接.
- ✅使用添加引用.
- ⬛️重要概念框.
格式统一教程: 标题
随机引的名人名言, 用quote括起 – 译者, 2025
学习目标
- 此处填写学习目标
- 一些目标
- 二些目标
- 三些目标
目录
以下是教程正文.
-
每一章以一些插图引入比较合适, 如下图, 然后再写正文前的引子.
-
使用
<span>即可添加能够超链接的ID (源码:[引用](#templateimage)), 点击即可跳转. -
原文中用斜体强调的词, 在译文中统一用加粗, 如:
You might think that the “best” algorithm for multiplying numbers will differ if you implement it in Python on a modern laptop than if you use pen and paper.
译作
例如, 你也许会认为, 在现代笔记本电脑上用 Python 实现的乘法算法, 与用纸笔进行乘法运算时的“最佳“算法会有所不同.
- 对某一章的引用可以直接引
.md: 例如本章 ([本章](chapter_x.md)), 对章节的引用则使用html id语法糖, 如下方x.1小节([x.1小节](#templatesection))所示.
x.1 小节: 右侧花括号添加 #id 即可用于引用
-
渲染时看不到上面说的花括号, 实际语句是:
## x.1 小节: 右侧花括号添加 #id 即可用于引用 { #templatesection } -
quote 可以带标题, 遵照原文即可. 当原文需要引用的时候, 就使用 quote.
举例来说: “一个平方加上它的十倍平方根等于三十九迪拉姆. “ 换句话说, 求这样一个平方数: 它加上它自身的十倍平方根, 结果是三十九.
解法如下:
(见Chapter 3)
因此, 这个平方根为三, 对应的平方为九.
- 代码块照常写即可.
# 使用 Python 的 sqrt 函数来计算平方根
def solve_eq(b, c):
# 根据 al-Khwarizmi 的方法求解 x^2 + b*x = c
blablabla()
# 测试: 求解 x^2 + 10*x = 39
print(solve_eq(10, 39))
-
出现在公式中的函数名全部应该用
\text框起, 如 ($\text{XOR}$). 如果发现某个名字经常出现, 应该将其添加进./makros.txt. 如与( 或( 非( ($\AND, \OR, \NOT$) -
example 环境的示例. 注意其中嵌套了代码, 所以使用了
~~~取代 ```. admonish的title中如果需要使用公式, 反斜杠需要重复三次. 例如下方的标题就出现了$\\\text{MAJ}$.
考虑函数 其定义如下:
(…)
我们也可以将公式 (3.1) 以“编程语言“的形式表示: 将其表达为一组指令, 用于在给定基本操作 的情况下计算
def MAJ(X[0],X[1],X[2]):
firstpair = AND(X[0],X[1])
secondpair = AND(X[1],X[2])
thirdpair = AND(X[0],X[2])
temp = OR(secondpair,thirdpair)
return OR(firstpair,temp)
- 公式的引用: 在行间公式中添加
[{numeq}]{id}, 例如: 然后就可以直接引用: (1) ([{eqref: templatenumeq}])(为防止替换, 这里最外层的花括号替换成了方括号.)
x.1.1 依然是小节名示例. 小节名总是可以添加id.
- 所有 preprocessor
numthm引入的定理/例子/命题环境都需要套一个 admonish quote, 以和正文分隔开.book.toml中可以自定义这些环境. 已经定义了一些“常用缩写+c“为名的中文环境. 例如:
引理 1. 对于每个 在输入 时, 算法 3.1 输出
-
numthm的引用方式: 引理 1 ([{ref: templatelem}]) (为防止替换, 这里最外层的花括号替换成了方括号.) -
小练习对应的 admonish solution 以及证明对应的 admonish proof 应该是 collapsible 的. 如:
解答
解答
我们可以通过枚举 的所有 种可能取值来证明这一点, 但它也可以直接从标准的分配律推导出来.
假设我们将任意正整数视为“真“, 将零视为“假“. 那么对于每个数 为正当且仅当 为真, 而 为正当且仅当 为真.
这意味着对于每个 表达式 为真当且仅当 为正, 而表达式 为真当且仅当 为正.
根据标准的分配律 因此前者表达式为真当且仅当后者表达式为真.
对[{ref:id}]的证明
对[{ref:id}]的证明
对于任意 有 当且仅当 与 不同.
令 则在输入 时, 算法 3.1 输出
-
如果 则 因此输出为
-
如果 则 所以 输出为
-
如果 且 (或反之) , 则 且 此时算法输出
- 原文的 pause 也有对应的 admonish:
- 算法的写法, 以下是一个例子:
当然, 与图片一样, 也可以使用llm帮助转换.
依照示例, 将以下格式的算法转换为tex格式:
Input: $a,b \in \{0,1\}.$
Output: $XOR(a,b)$
$w1 \leftarrow AND(a,b)$
$w2 \leftarrow NOT(w1)$
$w3 \leftarrow OR(a,b)$
return $AND(w2,w3)$
转换为
$
\begin{array}{l}
\mathbf{Input:}\ a,b \in \{0,1\} \\
\mathbf{Output:}\ \XOR(a,b) \\
\hline
\mathbf{Step 1:}\ w_1 \leftarrow \AND(a,b) \\
\mathbf{Step 2:}\ w_2 \leftarrow \NOT(w_1) \\
\mathbf{Step 3:}\ w_3 \leftarrow\OR(a,b) \\
\mathbf{Step 4: return}\ \AND(w_2,w_3)
\end{array}
$
我将提供其它类似格式的算法输入.
-
脚注的例子 1 (
[{footnote: 这是一条脚注}]). 最外层的方括号替换为花括号, 文中出现脚注时需要使用. -
正文结束后, 用 admonish hint 写回顾
x.2 小节: 各类环境使用方式汇总
x.2.1 admonish
- 插入图片: 用pic环境框起, 再付一个numthm的pic编号环境. 源码:
```admonish pic id = '图片id'

<-- 这里的空行不能省
[{pic}] 图片描述 <-- 外层花括号改为方括号, 和描述之间的空格不能省
```
效果如下, 引用可直接使用pic id:
图 1. 这是图片描述.
插入图片的格式可以设计prompt交给llm处理. 下面给一个例子
请根据以下例子转换插入图片的格式:
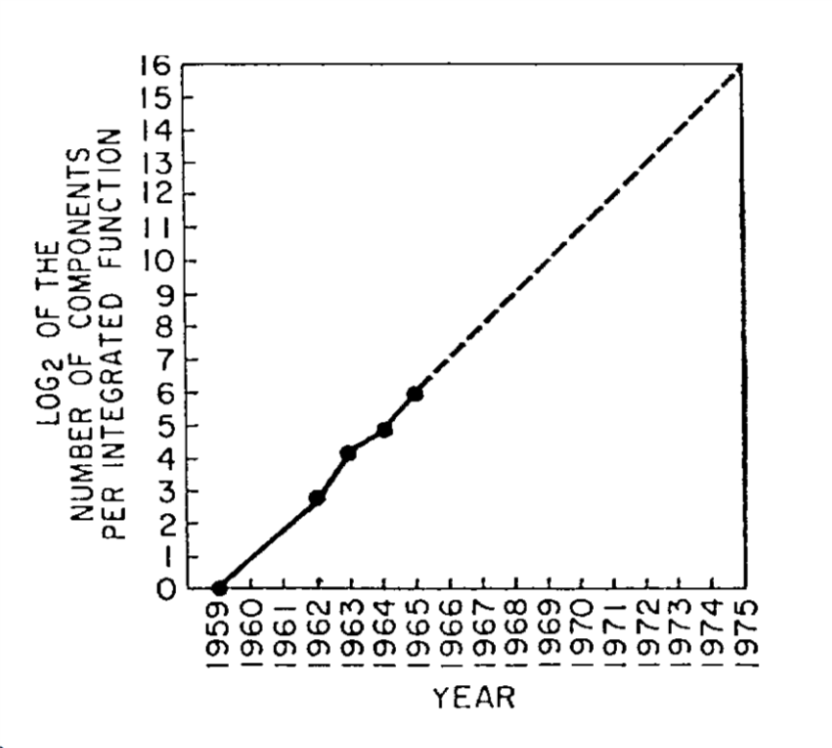{#moorefig .margin}
转换为
```admonish pic id = "moorefig"

[{pic}] 1959 至 1965 年间集成电路中的晶体管数量,并预测指数级增长至少能持续十年。取自戈登·摩尔 1965 年的文章 *Cramming More Components onto Integrated Circuits*。
```
我将提供其它相同格式的代码, 输出请装在代码块内: 要再套一层代码块, 而不是使用已有的.
- 原文出现的 Big Idea(重要启示):
习题
- 习题的专有
numthm环境是proc. 例如:
- 依然可以先翻译习题(和标题), 再用llm调整格式, 以下是可用的prompt.
改变以下我输入的习题框的格式: 例如
::: {.exercise title="比较 $4$bit 数字" #comparenumbersex}
给出一个布尔电路(使用 $\AND/\OR/\NOT$ 门),该电路计算函数 $ \text{CMP}_8:\{0,1\}^8 \rightarrow \{0,1\}$,使得当且仅当由 $a_0a_1a_2a_3$ 表示的数大于由 $b_0b_1b_2b_3$ 表示的数时,$ \text{CMP}_8(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)=1$。
:::
改为
[{proc}]{comparenumbersex}[比较 $4$bit 数字]
给出一个布尔电路(使用 $\AND/\OR/\NOT$ 门),该电路计算函数 $ \text{CMP}_8:\{0,1\}^8 \rightarrow \{0,1\}$,使得当且仅当由 $a_0a_1a_2a_3$ 表示的数大于由 $b_0b_1b_2b_3$ 表示的数时,$ \text{CMP}_8(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)=1$。
接下来我将提供输入.
注意上面proc的方括号要改掉.
杂记
- 杂记需要修复对文献的引用. 使用
<a>编写引用.
未完成章节中的引用:
以下是未完成的章节中的引用
1: 这是一条脚注