- 等价的计算模型
等价的计算模型
学习目标
- 了解RAM机(RAM Machine)与λ演算(λ Calculus)
- 掌握这些模型与图灵机及其他模型的等价关系
- 认识元胞自动机(Cellular Automata)与各种图灵机格局
- 理解Church-Turing论题
由于后续我们将使用函数表达式进行计算, 必须区分函数与形式, 并需要相应的表示法. 这一区分及其描述记法由Church提出, 我们仅作细微调整.
——约翰·麦卡锡(John McCarthy), 1960年(摘自描述LISP编程语言的论文)
到目前为止, 我们已经定义了使用图灵机计算函数的概念, 但这与实际的计算方法并不完全吻合. 本章将通过证明可计算函数的定义在各种计算模型下保持不变, 来论证这一选择的合理性. 这一概念被称为图灵完备性(Church completeness)或图灵等价性(Church equivalence), 是计算机科学中最基本的事实之一. 实际上, 被广泛认同的Church-Turing论题做了出了如下主张: 任何对可计算函数的“合理“定义, 都等价于通过图灵机可计算的概念. 我们将在8.8节讨论Church-Turing论题以及“合理“的可能定义.
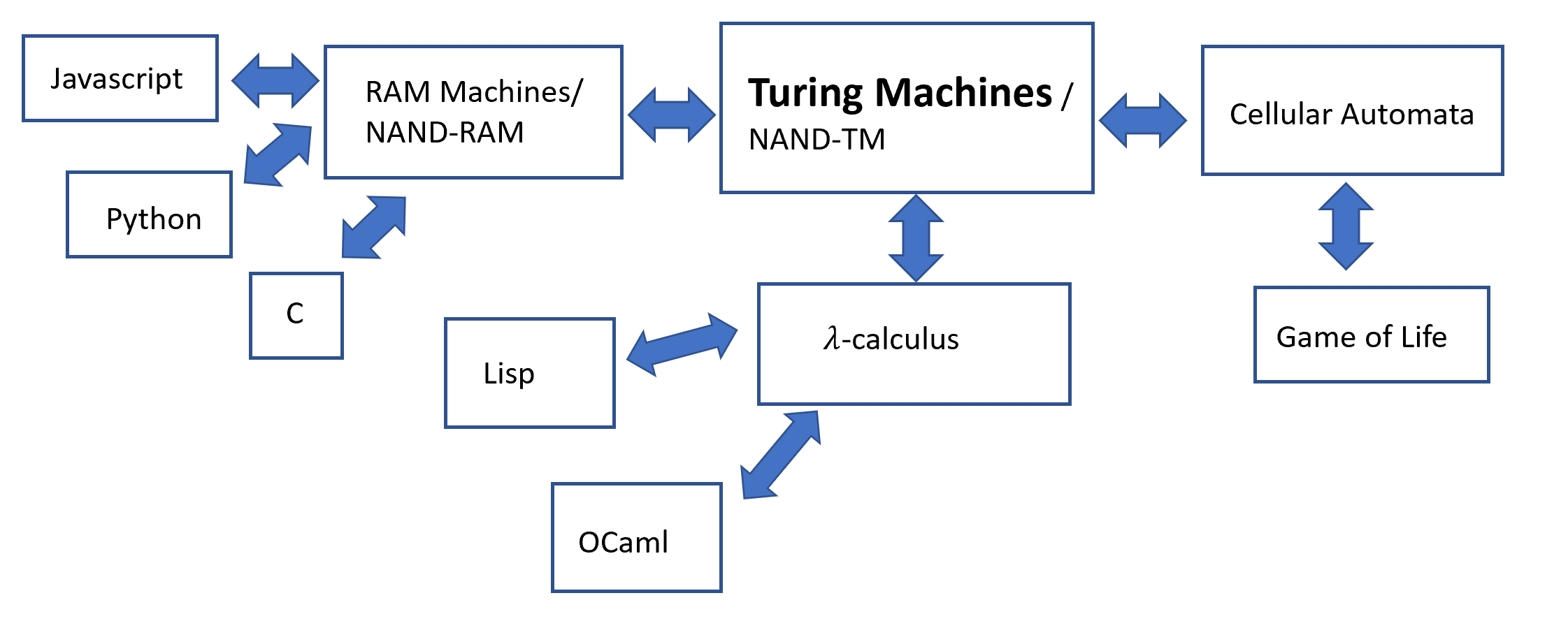
本章讨论的主要计算模型包括:
- RAM机: 图灵机与具备随机存取存储器(RAM, Random Access Memory)的标准计算架构并不对应, RAM机的数学模型更接近实际计算机, 但我们将看到它在计算能力上与图灵机等价. 我们还将讨论RAM机的一种编程语言变体, 称之为NAND-RAM. 图灵机与RAM机的等价性使得我们能够证明诸多流行编程语言的图灵等价性, 包括现实中使用的所有通用编程语言, 如C、Python、JavaScript等.
- 元胞自动机: 许多自然的和人工的系统都可以被建模为简单组件的集合, 每个组件根据其自身状态及其直接邻居的状态, 按照简单的规则进行演化. 一个著名的例子是康威的生命游戏(Conway’s Game of Life). 为了证明元胞自动机与图灵机等价, 我们将引入图灵机格局(configurations of Turing machines). 这些格局还有其他应用, 特别是在第11章用于证明哥德尔不完备定理——数学中的一个核心结果.
- λ演算: λ演算是一种表达计算模型, 起源于20世纪30年代, 不过它与当今广泛使用的函数式编程语言密切相关. 证明λ演算与图灵机等价涉及一种名为“Y组合子“(Y Combinator)的消除递归的巧妙方法.
本章中我们将研究不同模型间的等价性. 如果两个计算模型能够计算的函数构成的集合是相同的, 则称它们是等价的(也称之为图灵等价). 例如, 我们已经看到图灵机与NAND-TM程序是等价的, 因为我们可以将每个图灵机转换为计算相同函数的NAND-TM程序, 同样地, 也可以将每个NAND-TM程序转换为计算相同函数的图灵机.
本章我们将证明这种等价性远不止于图灵机. 我们开发的技术使我们能够证明所有通用编程语言(即Python、C、Java等)都是图灵完备的, 即它们能够模拟图灵机, 因此能够计算所有图灵机可计算的函数. 我们还将证明其反向亦成立——图灵机可以用来模拟用任何这些语言编写的程序, 因此能够计算这些语言可计算的任何函数. 这意味着所有这些编程语言都是图灵等价的: 即它们在计算能力上等价于图灵机, 并且彼此等价. 这是一个强大的原理, 是计算机科学广泛影响的基础. 此外, 它使我们能够“鱼和熊掌兼得“——既然所有这些模型都是等价的, 我们可以为手头的任务选择方便的模型. 为了实现这种等价性, 我们定义了一种新的计算模型, 称为RAM机. RAM机比图灵机更接近现代计算机的架构, 但在计算能力上仍然与图灵机等价.
最后, 我们将证明图灵等价性远不止于传统编程语言, 作为极其简单的自然系统的数学模型的元胞自动机也是图灵等价的, 并且我们还将看到λ演算的图灵等价性——λ演算是一种用于表达函数的逻辑系统, 是Lisp、OCaml等函数式编程语言的基础.
本章成果概览见图 8.1.
8.1 RAM机与NAND-RAM
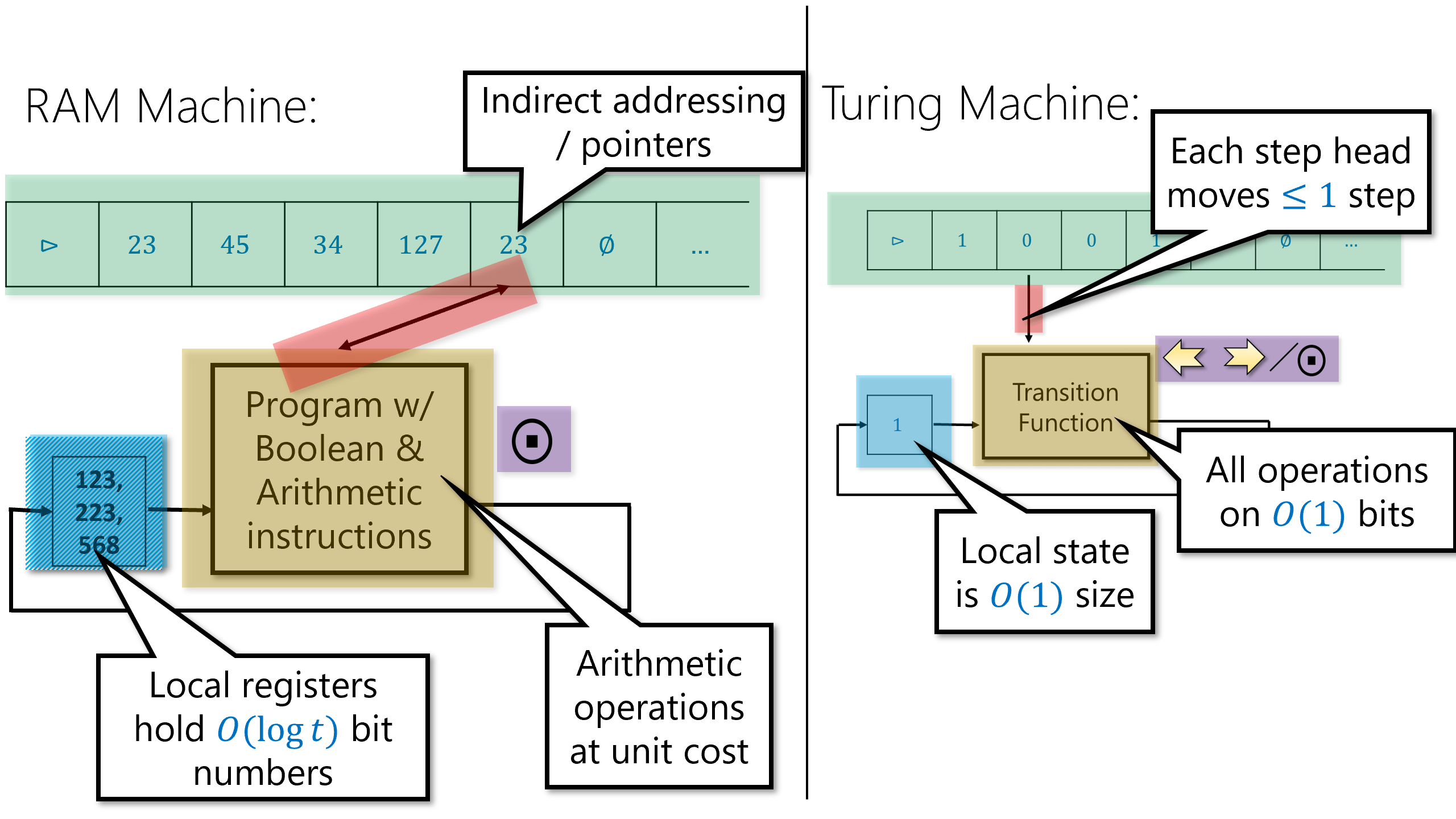
图灵机(以及NAND-TM程序)的一个局限性在于, 我们每次只能访问数组或磁带的一个位置. 如果磁头位于磁带的第位, 而我们想要访问第个位置, 那么我们至少需要步才能到达该位置. 相比之下, 几乎每种编程语言都提供了直接访问内存位置的形式化方法. 实际的物理计算机也提供了可以被视为一个大型数组Memory的随机存取存储器(RAM), 给定索引(即内存地址或指针), 我们可以读取和写入Memory的第个位置. (“随机存取存储器“这一名称实际上用词有误, 因为它与概率无关, 但既然这是计算理论与实践中的标准术语, 我们也将沿用这一说法).
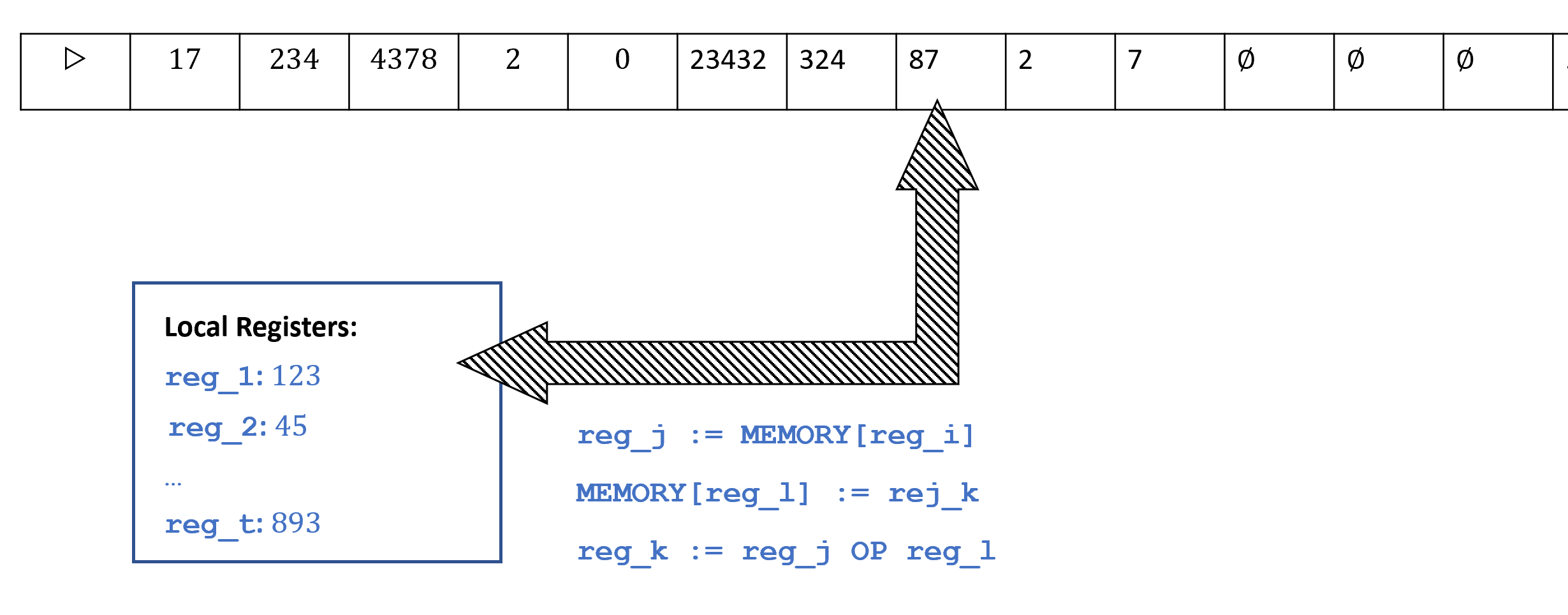
中这种内存访问进行建模的计算模型是RAM机(有时也称为字RAM模型(Word RAM Model)), 如图 8.2所示. RAM机的内存是一个大小无界的数组, 其中每个单元可以存储一个字(Word), 我们将其视为的字符串, 同时(等价地)也视为中的一个数字. 例如, 许多现代计算架构使用64位的字, 每个内存位置保存一个中的字符串, 这也可以视为一个介于到之间的数字. 参数被称为字长(Word Size). 在实践中, 通常是一个固定数字(比如64), 但在理论研究中, 我们将建模为一个可以依赖于输入长度或步骤数的参数. (你可以将大致视为我们在计算中使用的最大内存地址)除了内存数组, RAM机还包含恒定数量的寄存器(Register) 每个寄存器也能保存一个字.
RAM机可以执行的操作包括:
- 数据移动: 将内存中某个单元的数据加载到寄存器中, 或将寄存器的内容存储到内存的某个单元. RAM机可以直接访问内存的任何单元, 而无需像图灵机那样将“磁头“移动到该位置. 也就是说, RAM机可以在一步中将由寄存器索引的内存单元的内容加载到寄存器中, 或将寄存器的内容存储到由寄存器索引的内存单元中.
- 计算: RAM机可以对寄存器执行计算, 例如算术运算、逻辑运算和比较.
- 控制流: 与图灵机一样, 接下来执行什么指令的选择可以取决于RAM机的状态, 这由其寄存器的内容捕获.
我们不会给出RAM机的正式定义, 但参考文献部分(第8.10节)包含了这些定义的来源. 正如NAND-TM编程语言模拟图灵机一样, 我们也可以定义一种模拟RAM机的NAND-RAM编程语言. NAND-RAM编程语言通过添加以下特性扩展了NAND-TM:
- NAND-RAM的变量允许是(非负)整数值的, 而不仅仅是NAND-TM中的布尔值. 也就是说, 标量变量
foo保存的是中的非负整数(而不仅仅是中的一位), 数组变量Bar保存的是一个整数数组. 与RAM机的情况一样, 我们不允许无界大小的整数. 具体来说, 每个变量保存一个介于和之间的数字, 其中是程序到目前为止已执行的步骤数. (你现在可以忽略此限制: 如果我们想要保存更大的数字, 可以简单地执行虚拟指令;这在后面的章节中会有用) - 我们允许对数组进行索引访问. 如果
foo是标量而Bar是数组, 则Bar[foo]引用由foo的值索引的Bar的位置. (注意这意味着我们不再需要特殊的索引变量i) - 正如编程语言中常见的情况, 我们假设对于布尔运算(如
NAND), 零值整数被视为假, 非零值整数被视为真. - 除了
NAND之外, NAND-RAM还包括所有基本的算术运算: 加、减、乘、(整数)除, 以及比较(等于、大于、小于等). - NAND-RAM将条件语句
if/then作为语言的一部分. - NAND-RAM包含循环结构, 例如
while和do, 作为语言的一部分.
NAND-RAM编程语言的完整描述见附录. 然而, 关于NAND-RAM你需要了解的最重要的事实是你实际上并不需要太多了解NAND-RAM, 因为它在能力上等同于图灵机:
由于NAND-TM程序等价于图灵机, 而NAND-RAM程序等价于RAM机, 定理 8.1表明所有这四种模型彼此之间是等价的.
定理 8.1的证明思路
定理 8.1的证明思路
显然, NAND-RAM只会比NAND-TM更强大, 因此如果一个函数可由NAND-TM程序计算, 那么它也能由NAND-RAM程序计算. 具有挑战性的方向是将NAND-RAM程序转换为等价的NAND-TM程序 要完整描述这个证明, 我们需要涵盖NAND-RAM语言的完整形式化规范, 并展示如何将其每一个特性实现为NAND-TM之上的语法糖.
这可以做到, 但详细检查所有操作相当繁琐. 因此, 我们将着重描述此转换背后的主要思想. (另见图 8.4)NAND-RAM在两个方面推广了NAND-TM: (a) 增加了对数组的索引访问(即Foo[bar]语法), 以及 (b) 从布尔值变量过渡到整数值变量. 该转换有两个步骤:
- 位数组的索引访问: 我们首先展示如何处理 (a). 即, 我们展示如何在NAND-TM中实现操作
Setindex(Bar), 使得如果Bar是编码了某个整数的数组, 则在执行Setindex(Bar)后,i的值将等于 这将允许我们通过Setindex(Bar)后跟Foo[i]来模拟Foo[Bar]这种形式的语法. - 二维位数组: 接着, 我们展示如何使用“语法糖“来为NAND-TM增加二维数组的功能. 即, 拥有两个索引
i和j以及二维数组, 使得我们可以使用语法Foo[i][j]来访问Foo的(i,j)位置. - 整数数组: 最后, 我们将一个整数的一维数组
Arr编码为一个位的二维数组Arrbin. 思路很简单: 如果是Arr[]的一个二进制(无前缀)表示, 那么Arrbin[][]将等于
一旦我们有了整数数组, 我们就可以使用我们常用的函数语法糖、GOTO等来实现NAND-RAM的算术和控制流操作.
上述方法并非获得定理 8.1证明的唯一途径, 例如可参见练习8.1.
RAM机与现实中的微处理器(例如Intel x86系列中的那些)非常对应, 这些微处理器也包含一个大的主内存和数量固定的少量寄存器. 这当然并非偶然: 与图灵机相比, RAM机旨在更贴近地模拟实际计算系统的体系结构, 这种体系结构在很大程度上遵循了 (von Neumann, 1945) 报告中描述的所谓冯·诺依曼架构. 因此, NAND-RAM在其大致轮廓上类似于x86或NIPS等汇编语言. 这些汇编语言都具有以下指令: (1) 将数据从寄存器移动到内存, (2) 对寄存器执行算术或逻辑计算, 以及 (3) 条件执行和循环(在汇编语言语境中通常称为“分支“和“跳转“的“if“和“goto“).
RAM机与实际微处理器之间的主要区别(相应地, 也是NAND-RAM与汇编语言之间的主要区别)在于, 实际微处理器具有固定的字长 因此所有寄存器和内存单元保存的都是中的数字(或等价地, 中的字符串). 这个数字在不同的处理器中可能不同, 但常见的值要么是 要么是 作为理论模型, RAM机没有这个限制, 我们反而让作为我们运行时间的对数(这也大致对应于其在实践中的值). 现实中的微处理器也具有固定数量的寄存器(例如, x86-64中有14个通用寄存器), 但这与RAM机相比差别不大. 可以证明, 只有两个寄存器的RAM机与拥有任意大的常数数量寄存器的完整RAM机具有同等能力.
当然, 现实中的微处理器也具有许多RAM机所不具备的特性, 包括并行性、内存层次结构以及许多其他特性. 然而, RAM机确实在初步近似下捕捉了实际计算机的特征, 因此(正如我们将看到的), 算法在RAM机上的运行时间(例如, 对比与其实际运行的效率高度相关.
8.2 具体细节(可选)
我们将不展示定理 8.1的完整形式化证明, 而是聚焦于最重要的部分: 实现索引访问, 以及用一维数组模拟二维数组. 即便如此, 描述这些部分也已经相当繁琐, 这对于任何写过编译器的人都不足为奇. 因此, 你可以随意略读本节. 重点不在于记住所有细节, 而在于明白原则上将一个NAND-RAM程序转换为等价的NAND-TM程序是可能的, 你自己如果想做也能完成.
8.2.1 NAND-TM中的索引访问
在NAND-TM中, 我们只能访问数组在索引变量i位置处的元素, 而NAND-RAM拥有整数值变量, 并能使用它们对数组进行索引访问, 写作Foo[bar]. 为了在NAND-TM中实现索引访问, 我们将使用某种无前缀编码(参见2.5.2节)在数组中编码整数, 然后提供一个过程Setindex(Bar)来将i设置为Bar编码的值. 我们可以通过先执行Setindex(Bar)再执行Foo[i]来模拟Foo[Bar]的效果.
Setindex(Bar)的实现可以通过以下方式完成:
- 初始化一个数组
Atzero, 使得Atzero[]并且对所有Atzero[](这可以在NAND-TM中轻松完成, 因为所有未初始化的变量默认值为零) - 通过递减
i直到达到Atzero[i]的点来将i设置为零. - 令
Temp为一个编码数字的数组. - 我们使用
GOTO来模拟一个内部循环, 形式如下: 当TempBar时, 递增Temp. - 在循环结束时,
i等于由Bar编码的值.
在NAND-TM代码中(使用一些语法糖), 我们可以按如下方式实现上述操作:
# 假设Atzero是一个数组, 满足Atzero[0]=1
# 且对所有j>0, Atzero[j]=0
# 将i设置为0.
LABEL("zero_idx")
dir0 = zero
dir1 = one
# 对应i <- i-1
GOTO("zero_idx",NOT(Atzero[i]))
...
# 将temp清零
#(下面的代码假设使用一种特定的无前缀编码, 其中10是"结束标记")
Temp[0] = 1
Temp[1] = 0
# 将i设置为Bar, 假设我们知道如何递增和比较
LABEL("increment_temp")
cond = EQUAL(Temp,Bar)
dir0 = one
dir1 = one
# 对应i <- i+1
INC(Temp)
GOTO("increment_temp",cond)
# 如果执行到这里, i就是Bar所编码的数字
...
# 程序的最终指令
MODANDJUMP(dir0,dir1)
8.2.2 NAND-TM中的二维数组
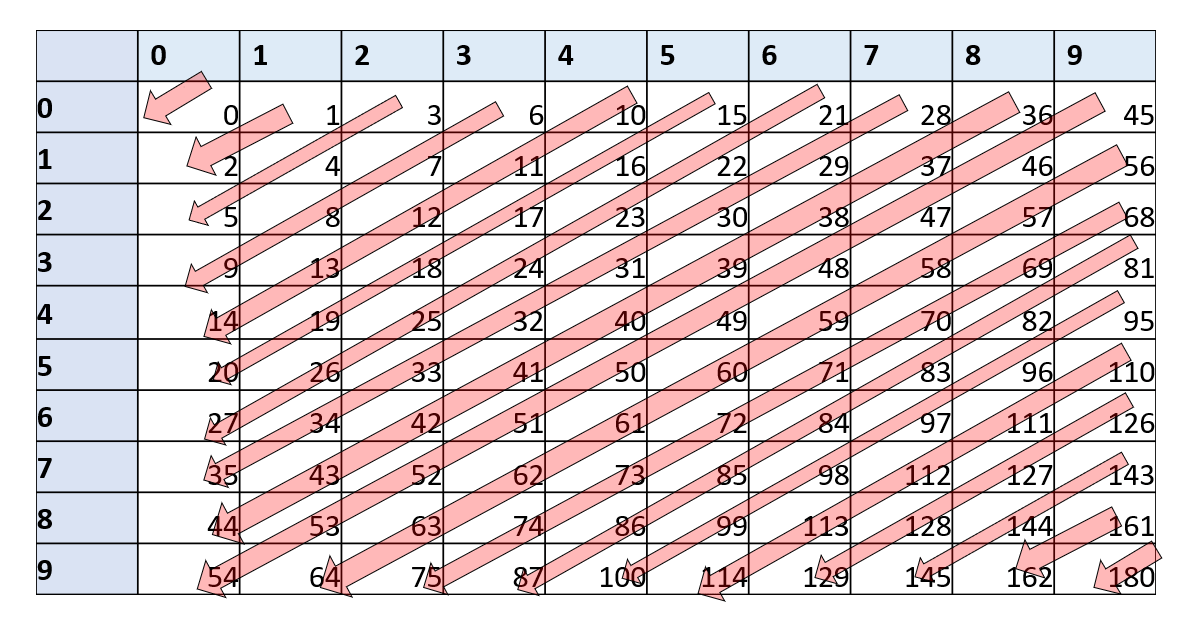
为了实现二维数组, 我们希望将它们嵌入到一个一维数组中. 思路是通过一个一一对应的函数 从而将二维数组Two中的位置嵌入到一维数组One的位置中.
由于集合看上去“远大于“集合 先验地来看, 这样的一个双射可能并不明显存在. 然而, 一旦你深入思考, 你就会发现构建它并不算太难. 例如, 你可以让一个孩子用剪刀和胶水将一张10英寸乘10英寸的纸转换成一条1英寸乘100英寸的纸带. 这本质上就是一个从到的双射. 我们可以推广这一点, 得到一个从到的双射, 更一般地, 得到一个从到的双射.
具体来说, 下面的函数可以做到这一点(见图 8.5):
习题8.3要求你证明确实是一个双射, 并且可以由一个NAND-TM程序计算. (后者可以通过简单地遵循小学所学的乘法、加法和除法算法来完成)这意味着我们可以将形式为Two[Foo][Bar] = something(即, 访问二维数组中由一维数组Foo和Bar编码的整数对应的位置)替换为如下形式的代码:
Blah = embed(Foo,Bar)
Setindex(Blah)
Two[i] = something
8.2.3 其他细节
一旦我们有了二维数组和索引访问, 用NAND-TM模拟NAND-RAM就只是在NAND-TM中实现算术运算和比较的标准算法的问题了. 虽然这很繁琐, 但并不困难, 最终的结果表明每个NAND-RAM程序都可以被一个等价的NAND-TM程序模拟, 从而完成了定理 8.1的证明.
递归是许多编程语言中都出现的一个概念, 但我们没有将其包含在NAND-RAM程序中. 然而, 递归(以及一般的函数调用)可以在NAND-RAM中使用栈数据结构来实现. 栈是一种包含一系列元素的数据结构, 我们可以按照“后进先出“的顺序向其中“压入“元素和从中“弹出“元素.
我们可以使用一个整数数组Stack和一个标量变量stackpointer(表示栈中的项目数量)来实现一个栈. 我们通过以下方式实现push(foo):
Stack[stackpointer]=foo
stackpointer += one
并通过以下方式实现bar = pop():
bar = Stack[stackpointer]
stackpointer -= one
我们通过将的参数压入栈中来实现对的函数调用. 的代码将从栈中“弹出“参数, 执行计算(可能涉及进行递归或非递归调用), 然后将其返回值“压入“栈中. 由于栈的“后进先出“特性, 直到所有递归调用完成, 我们才会将控制权返回给调用过程.
我们可以使用非递归语言实现递归这一事实并不令人惊讶. 实际上, 机器语言通常不具有递归(或一般的函数调用)功能, 因此编译器使用栈和GOTO来实现函数调用. 你可以在网上找到关于您最喜欢的编程语言(无论是Python、JavaScript还是Lisp/Scheme)中如何通过栈实现递归的教程.
8.3 图灵等价性(讨论)
任何标准编程语言, 如C、Java、Python、Pascal、Fortran, 其操作都与NAND-RAM非常相似. (事实上, 它们最终都可以由具有固定数量寄存器和大型内存阵列的机器来执行)因此, 使用定理 8.1, 我们可以用NAND-TM程序来模拟任何此类编程语言中的程序. 反过来, 在任何上述编程语言中编写一个NAND-TM的解释器是一个相当简单的编程练习. 因此, 我们也可以使用这些编程语言来模拟NAND-TM程序(进而通过定理7.11来模拟图灵机). 这种在计算能力上等同于图灵机/NAND-TM的特性被称为图灵等价(有时也称为图灵完备). 因此, 我们熟悉的所有编程语言都是图灵等价的. 1
8.3.1 “两全其美“的范式
图灵机与RAM机之间的等价性使我们能够为手头的任务选择最方便的语言:
- 当我们想要证明一个关于所有程序/算法的定理时, 我们可以使用图灵机(或NAND-TM), 因为它们更简单且易于分析. 特别是, 如果我们想证明某个函数无法被计算, 那么我们将使用图灵机.
- 当我们想要证明某个函数可以被计算时, 我们可以使用RAM机器或NAND-RAM, 因为它们更容易编程, 并且更接近于我们习惯的高级编程语言. 事实上, 我们通常会以非正式的方式描述NAND-RAM程序, 并相信读者能够填充细节并将简略的描述转换为精确的程序. (这就像人们通常使用非正式的或“伪代码“的算法描述方式, 并相信他们的受众知道在需要时将这些描述转换为代码一样)
我们对图灵机/NAND-TM和RAM机/NAND-RAM的使用, 与人们在实践中使用高级和低级编程语言的方式非常相似. 当人们想要制造一个执行程序的设备时, 为一种非常简单和“低级“的编程语言来实现是很方便的. 当人们想要描述一个算法时, 使用尽可能高级的形式体系是方便的.
8.3.2 浅谈抽象层次
程序员处于一个独特的位置……他必须能够思考概念层次结构, 其深度是单个思维以前从未需要面对的.
*——Edsgar Dijkstra, 《论真正教授计算机科学的残酷性》, 1988年. *
在任何计算理论课程中的某个时刻, 教师和学生都需要进行那次谈话. 也就是说, 我们需要讨论描述算法时的抽象层次. 在算法课程中, 通常用英语描述算法2, 假设读者能够“填充细节“, 并在需要时能够将此类算法转化为实现. 例如, 算法 8.1是广度优先搜索算法的高级描述.
如果我们想提供关于如何在Python或C(或NAND-RAM/NAND-TM)等编程语言中实现广度优先搜索的更多细节, 我们会描述如何用数组实现队列数据结构, 以及同样如何用数组标记顶点. 我们称这种“中间层次“的描述为实现级别(implementation level)或伪代码描述. 最后, 如果我们想精确地描述实现, 我们会给出程序的全部代码(或另一个完全精确的表示形式, 例如元组列表的形式). 我们称之为形式化或低级(low level)描述.
虽然我们开始时是在完全形式化的层面上描述NAND-CIRC、NAND-TM和NAND-RAM程序, 随着本书的深入, 我们将转向实现级别和高级别的描述. 毕竟, 我们的目标不是使用这些模型进行实际计算, 而是分析计算的一般现象. 也就是说, 如果你不理解高级描述如何转化为实际实现, “深入底层“通常是一个极好的练习. 计算机科学家最重要的技能之一就是能够在抽象层次结构中上下移动.
类似的区别也适用于将对象表示为字符串的概念. 有时, 为了精确起见, 我们会给出一个低级规范(low level specification), 确切说明一个对象如何映射到二进制字符串. 例如, 我们可能将个顶点的图的编码描述为长度为的二进制字符串, 通过说明我们将顶点集为的图映射到字符串 其中的第个坐标是当且仅当边存在于中. 我们也可以使用中间或实现级别的描述, 只需简单说明我们使用邻接矩阵表示法来表示图.
最后, 因为图(以及一般对象)的各种表示之间的转换可以通过NAND-RAM(因此也可以通过NAND-TM)程序完成, 所以在进行高级别讨论时, 我们也会避免关于表示的讨论. 例如, 图连通性是一个可计算函数, 这一事实无论我们是用邻接表、邻接矩阵、边对列表等表示图都是成立的. 因此, 在精确表示无关紧要的情况下, 我们通常会谈论我们的算法将对象(可以是图、向量、程序等)作为输入, 而不指定如何被编码为字符串.
定义“算法“: 到目前为止, 我们一直非正式地使用“算法“这个术语. 然而, 图灵机和一系列等效模型产生了一种精确且形式化地定义算法的方法. 因此, 在本书中, 每当我们提到算法时, 我们指的是它是图灵等效模型(如图灵机、NAND-TM、RAM机等)中的一个实例. 由于所有这些模型的等价性, 在许多情况下, 我们使用哪一个并不重要.
8.3.3 图灵完备性与等价性的形式化定义(可选)
一个计算模型是某种定义程序(由字符串表示)计算(部分)函数的方式. 一个计算模型是图灵完备的, 如果我们可以将每个图灵机(或等价的NAND-TM程序)映射到中的一个程序 使得计算与相同的函数. 它是图灵等价的, 如果另一个方向也成立(即, 我们可以将中的每个程序映射到一个计算相同函数的图灵机). 我们可以形式化地定义这个概念如下. (这个形式化定义对于本书的其余部分并不关键, 只要你理解图灵等价的一般概念就可以跳过它;这个概念在文献中有时被称为哥德尔数(Gödel numbering)或可接纳数(admissible numbering))
一些图灵等价模型的例子(其中一些我们已经见过, 一些将在下面讨论)包括:
- 图灵机
- NAND-TM程序
- NAND-RAM程序
- λ演算
- 生命游戏(将程序和输入/输出映射到起始和结束格局)
- 编程语言, 如Python/C/Javascript/OCaml…(允许无限存储)
8.4 元胞自动机
许多物理系统可以被描述为由大量相互作用的基元组件组成. 一种模拟此类系统的方法是使用元胞自动机. 这是一个由大量(甚至无限)细胞组成的系统. 每个细胞只有有限个可能的状态. 在每个时间步, 细胞通过将某个简单规则应用于自身及其邻居的状态来更新到新状态.
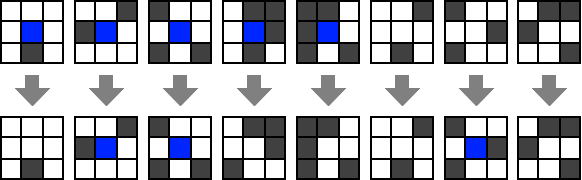
图 8.9. 康威生命游戏的规则. 图片来自此博客文章
元胞自动机的一个典型例子是康威的生命游戏(Conway’s Game of Life). 在此自动机中, 细胞排列在一个无限二维网格中. 每个细胞只有两种状态: “死亡”(我们可以编码为并标识为或“存活“(我们可以编码为 细胞的下一个状态取决于其先前状态及其8个垂直、水平和对角线邻居的状态(参见图 8.9). 死亡细胞只有在恰好有三个存活邻居时才会变为存活. 存活细胞只有在有两个或三个存活邻居时继续存活. 尽管细胞数量可能无限, 但我们可以通过仅跟踪存活细胞来使用有限长度字符串编码状态. 如果我们在具有有限数量存活细胞的格局中初始化系统, 那么在所有未来步骤中存活细胞的数量将保持有限. 生命游戏的维基百科页面上有一些产生非常有趣演化的格局的美丽图形和动画.
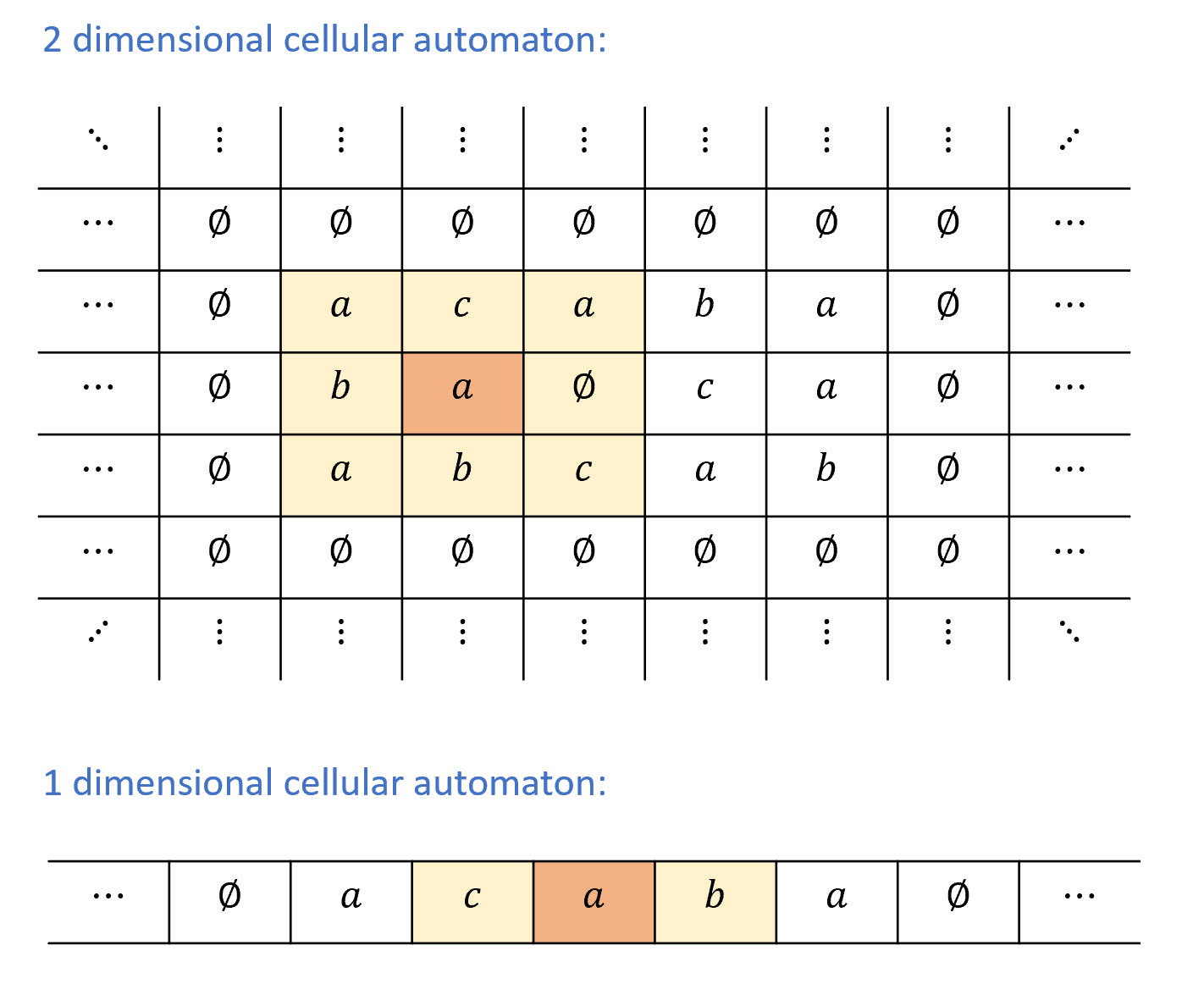
由于生命游戏中的细胞排列在无限二维网格中, 它是二维元胞自动机的一个例子. 我们也可以考虑一维元胞自动机的更简单设置, 其中细胞排列在一条无限直线上, 参见图 8.10. 事实证明, 即使这个简单模型也足以实现图灵完备性. 我们现在将正式定义一维元胞自动机, 然后证明它们的图灵完备性.
有限格局: 如果自动机的格局中只有有限个索引在中使得 则我们称该格局是_有限的_. (即, 对于每个 有这样的格局可以使用一个有限字符串表示, 该字符串编码索引和值 由于 如果是有限格局, 则也是有限的. 我们只关心在有限格局中初始化的元胞自动机, 因此在其整个演化过程中保持有限格局.
8.4.1 一维元胞自动机的图灵完备性
我们可以编写一个程序(例如使用NAND-RAM)来模拟任何元胞自动机从初始有限格局的演化, 只需存储状态不等于的细胞值并重复应用规则 因此, 元胞自动机可以被图灵机模拟. 更令人惊讶的是, 反过来也成立. 例如, 尽管其规则简单, 我们可以使用生命游戏模拟图灵机(参见图 8.11).
图 8.11. 模拟图灵机的生命游戏格局. 图片由Paul Rendell提供
事实上, 即使一维元胞自动机也可以是图灵完备的:
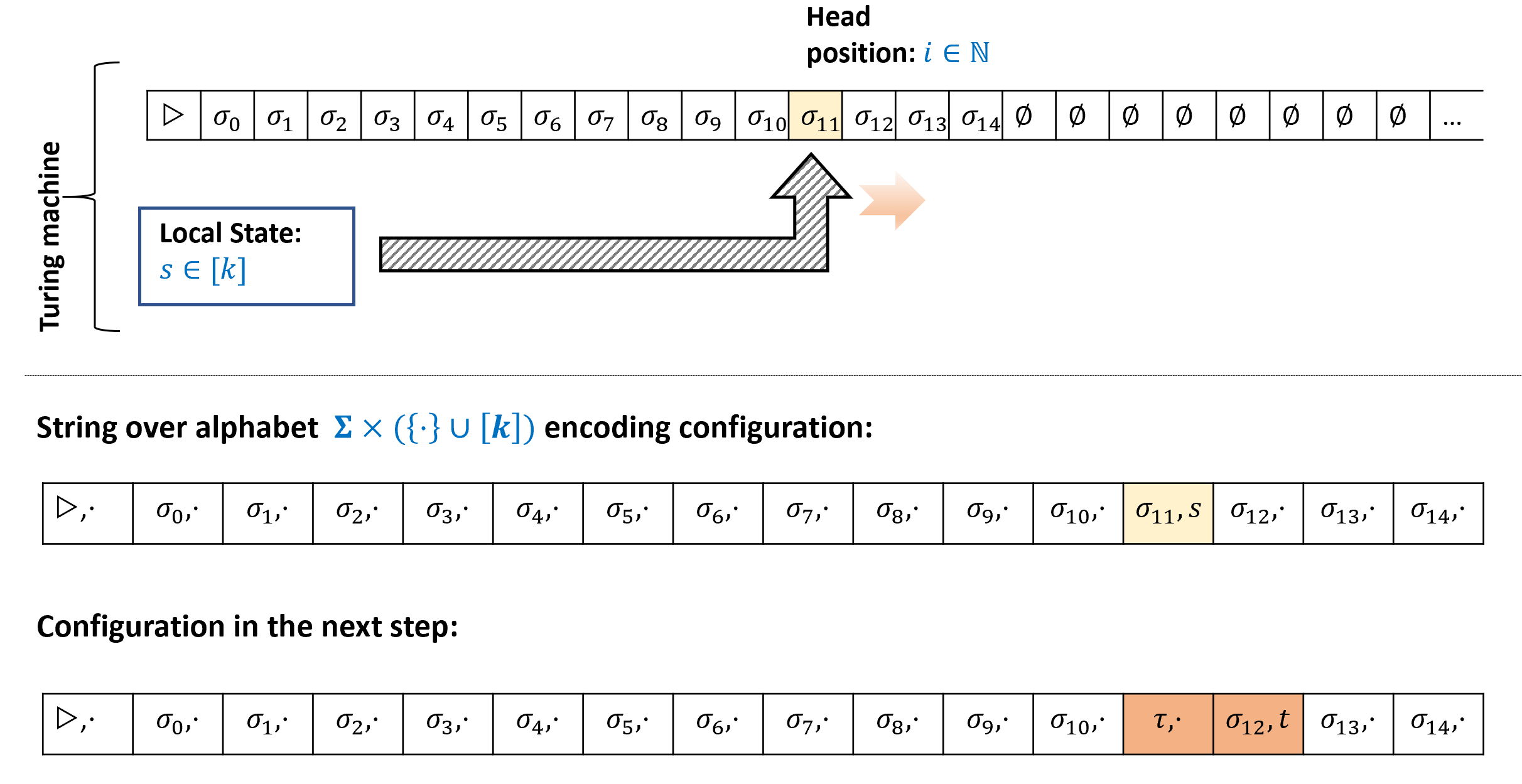
为了使“模拟图灵机“的概念更精确, 我们需要定义图灵机的格局. 我们将在下面的8.4.2节中这样做, 但高层面上, 图灵机的格局是一个字符串, 编码了其在计算中给定步骤的完整状态. 即, 其磁带所有(非空)单元的内容、其当前状态以及磁头位置.
定理 8.2的证明的关键思想是, 在图灵机的计算中的每个点, 的磁带中唯一能改变的单元是磁头所在的位置, 并且该单元改变的值是其当前状态和的有限状态的函数. 这一观察使我们能够将图灵机的格局编码为一个元胞自动机的有限格局, 并确保此编码格局在的规则下的一步演化对应于图灵机执行中的一步.
8.4.2 图灵机格局与状态转移函数
为了将上述思想转化为定理 8.2的严格证明(甚至陈述! ), 我们需要精确定义图灵机的格局这一概念. 这个概念在后续章节中对我们也有用.
定义 8.3有一些技术细节, 但实际上并不深奥或复杂. 尝试花点时间停下来思考你如何将图灵机在执行中给定点的状态编码为一个字符串.
思考你需要知道哪些组件才能从此点继续执行, 以及使用有限符号列表编码它们的简单方法是什么. 特别是, 考虑到我们未来的应用, 尝试思考一种编码, 使得将步骤的格局映射到步骤的格局尽可能简单.
定义 8.3有点繁琐, 但无论怎么讲格局只是一个字符串, 编码了图灵机在执行中给定点的快照. (用操作系统术语, 它是一个“核心转储“(core dump))这样的快照需要编码以下组件:
- 当前磁头位置.
- 大容量存储器的完整内容, 即磁带.
- “本地寄存器“的内容, 即机器的状态.
我们如何编码格局的精确细节并不重要, 但我们确实想记录以下简单事实:
(为简化记号, 上面我们使用约定: 如果“越界”, 例如或 则我们假设我们将引理 8.1的证明留作练习8.7. 证明背后的思想很简单: 如果磁头既不在位置 也不在位置和 那么处的下一步格局将与之前相同. 否则, 我们可以从或其邻居的格局中“读取“图灵机的状态和磁头位置的磁带值, 并用其更新处的新状态应该是什么. 完成完整证明并不难, 但这样做是确保你熟悉格局定义的好方法.
完成定理 8.2的证明: 我们现在可以更正式地重述定理 8.2, 并完成其证明:
从定理 8.3的证明中产生的自动机具有大的字母表, 而且其大小依赖于被模拟的机器 事实证明, 人们可以获得一个具有固定大小字母表的自动机, 该字母表独立于被模拟的程序, 实际上自动机的字母表可以是最小集合! 图 8.13展示了这样的一个图灵完备的自动机.

图 8.13. 一维自动机的演化. 图中的每一行对应一个格局. 初始格局对应顶行, 仅包含一个“存活“细胞. 此图对应Stephen Wolfram的“规则110“自动机, 它是图灵完备的. 图片取自Wolfram MathWorld
我们可以使用与定义 8.3相同的方法来定义NAND-TM程序的格局. 这样的格局需要编码:
- 变量
i的当前值. - 对于每个标量变量
foo,foo的值. - 对于每个数组变量
Bar, 值Bar[]对于每个 其中是指标变量i在计算中曾达到的最大值.
8.5 λ演算与函数式编程语言
λ演算是定义可计算函数的另一种方式. 它有Alonzo Church在1930年代提出, 大约与Alan Turing提出图灵机同时. 有趣的是, 尽管图灵机不用于实际计算, λ演算却催生了函数式编程语言, 如Lisp、ML和Haskell, 并间接地促进了许多其他编程语言的发展. 在本节中, 我们将介绍λ演算并展示其能力等价于NAND-TM程序(因此也等价于图灵机). 我们的Github仓库包含一个Jupyter Notebook, 其中有一个λ演算的Python实现, 你可以通过实验来更好地理解这个话题.
λ算子: λ演算的核心是定义“匿名“函数的一种方式. 例如, 有一个函数的定义为
我们可以将其写为
因此 也就是说, 你可以将(其中是某个表达式)视为指定匿名函数的一种方式. 匿名函数使用、或其他密切相关的表示法, 出现在许多编程语言中. 例如, 在Python中我们可以使用lambda x: x*x来定义平方函数, 而在JavaScript中我们可以使用x => x*x或(x) => x*x. 在Scheme中我们会将其定义为(lambda (x) (* x x)). 显然, 函数的参数名称无关紧要, 因此与相同, 因为两者都对应平方函数.
省略括号: 为了减少表示上的杂乱, 在书写λ演算表达式时我们经常省略函数求值的括号. 因此, 与其将函数应用于输入的结果写为 我们也可以简单地写为 因此我们可以写 在本章中, 我们将同时使用和表示法进行函数应用. 函数求值是结合性的, 并从左到右绑定, 因此与相同.
8.5.1 函数的高阶应用
λ演算的一个核心特性是函数都是“一等公民“, 即我们可以将函数作为其他函数的参数. 比如说, 你能猜到下面这个表达式等于什么数字吗?
(8.1)可能看上去有点吓人, 但在你看下面的解答之前, 尝试将其分解为各个组成部分, 并一次计算一个部分. 完成这个例题将极大地有助于理解λ演算
让我们一步一步地计算(8.1). 尽管允许匿名函数是λ演算的优势, 但添加名称对于理解复杂表达式非常有帮助. 因此, 我们令与
因此, (8.1)可以写作 在输入函数时, 输出函数 换而言之, 是函数 我们的函数是简单的 因此是将映射到的函数. 因此
8.5.2 通过柯里化实现多参数函数
在形如的λ表达式中, 表达式本身也可以包含λ运算符. 比如如下函数 将映射到函数
特别地, 若我们使用调用函数(8.3)得到某个函数 再以调用 便可获得值 可以看出, 对应于的单参数函数(8.3)亦可视为双参数函数 一般地, 我们可以使用λ表达式来模拟双参数函数的效果, 这一技巧被称为柯里化(Currying). 我们将使用作为的简写形式. 若 则对应于对进行求值后, 将所得函数作用于 从而获得将中出现处替换为 出现处替换为的结果. 根据结合律, 该结果等价于 有时我们也写作
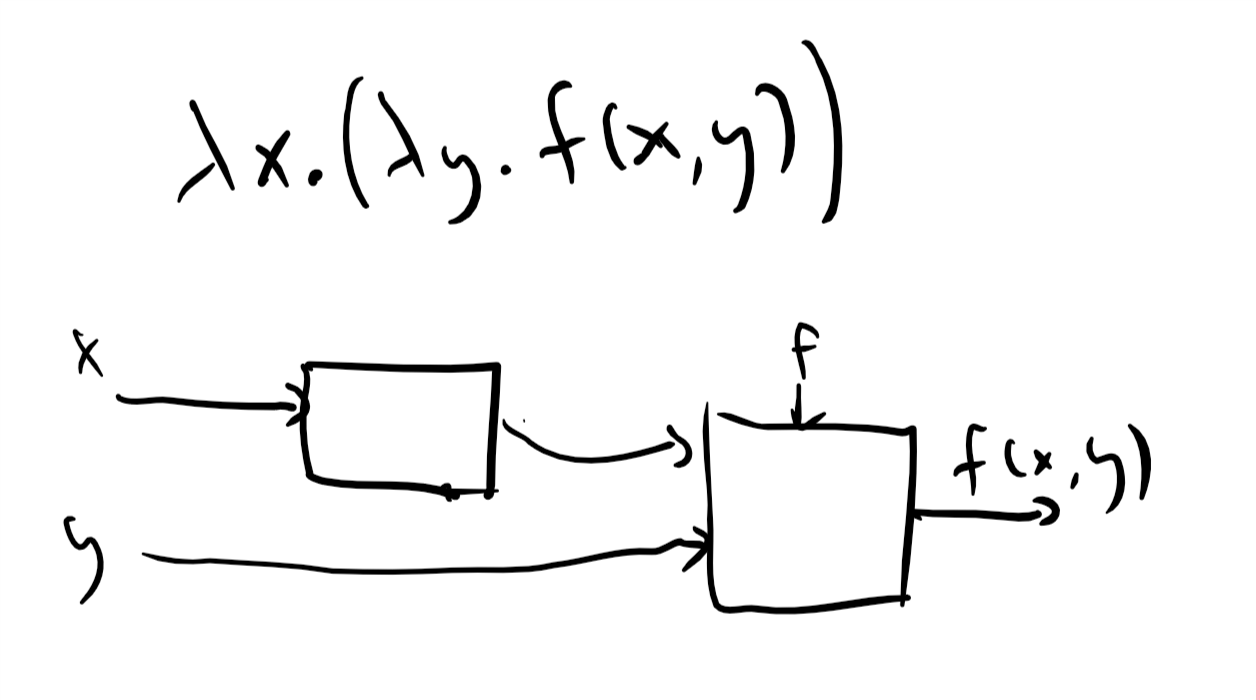
图 8.14. 在“柯里化“转换中, 我们可以通过λ表达式实现双参数函数的效果: 当输入时, 该表达式会输出一个单参数函数 其中已被“硬编码“至函数内, 且满足 这一过程可通过电路图直观展示, 详见Chelsea Voss的网站.
8.5.3 λ演算的形式化描述
我们现在提供λ演算的形式描述. 我们从包含单个变量的“基本表达式“开始, 例如或 并构建更复杂的表达式, 形为和 其中是表达式, 是变量标识符. 形式上, λ表达式的定义如下:
定义 8.4是一个递归定义, 因为我们在λ表达式的定义中使用了其自身. 这可能起初看起来令人困惑, 但事实上你从小学起就已经知道递归定义. 考虑我们如何定义算术表达式: 它是一个表达式, 要么只是一个数字, 要么具有形式 或 其中和是其他算术表达式.
自由变量和绑定变量: λ表达式中的变量可以是自由的(free)或绑定(bound)到一个运算符(在1.4.7节的意义上). 在单变量λ表达式中, 变量是自由的. 在应用表达式中, 自由和绑定变量的集合与底层表达式和的相同. 在抽象表达式中, 中的所有自由出现(free occurences)都被绑定到的运算符. 如果你觉得自由和绑定变量的概念令人困惑, 你可以通过为所有变量使用唯一标识符来避免所有这些问题.
优先级和括号: 我们将使用以下规则来允许我们省略一些括号. 函数应用从左向右结合, 因此与相同. 函数应用的优先级高于λ运算符, 因此与相同. 这类似于我们在算术运算中使用优先级规则来允许我们使用更少的括号, 比如表达式可以写成 如8.5.2节所述, 我们还使用简写表示 以及简写表示 这与使用λ表达式模拟多输入函数的“柯里化“转换很好地配合.
λ表达式的等价性: 正如我们在练习 8.1中看到的,规则等价于使我们能够修改λ表达式并获得更简单的等价形式. 另一个我们可以使用的规则是参数名称无关紧要, 因此与相同. 这些规则一起定义了λ表达式的等价性概念:
如果是一个形式为的λ表达式, 那么它自然对应于将任何输入映射到的函数. 因此, λ演算自然隐含了一个计算模型. 由于在λ演算中, 输入本身可以是函数, 我们需要决定以什么顺序求值一个表达式, 例如
对此有两种自然约定:
- 按名调用(Call-by-name, 即“惰性求值“): 我们通过先将右侧表达式作为输入代入左侧函数来求值(8.4), 得到然后从此继续.
- 按值调用(Call-by-value, 即“立即求值“): 我们先对右侧进行求值并得到 然后将其代入左侧得到来求值(8.4).
因为λ演算只有纯函数, 没有“副作用“, 所以在许多情况下顺序无关紧要. 事实上, 可以证明如果我们在两种策略中都得到一个确定的不可约表达式(irreducible expression)(例如, 一个数字), 那么它将是同一个. 然而, 为具体起见, 我们将始终使用“按名调用“(即惰性求值)顺序. (编程语言Haskell也做出了相同的选择, 尽管许多其他编程语言使用立即求值)形式上, 使用“按名调用“求值λ表达式的过程由以下过程描述:
对练习 8.2的解答
对练习 8.2的解答
的规范简化就是 为了计算的规范简化, 我们首先使用归约将代入中的 但由于在这个函数中根本未被使用, 我们简单地得到 它同样简化为
8.5.4 λ演算中的无限循环
与图灵机和NAND-TM程序类似, λ演算中的简化过程也可能进入无限循环. 例如, 考虑以下λ表达式
若我们尝试通过将左侧函数作用于右侧函数来简化(8.5), 则会得到另一个(8.5)的副本, 因此该过程永不休止. 在某些情况下, 求值顺序会影响表达式是否可被简化, 具体参见习题8.9.
8.6 增强λ演算
我们现在将λ演算作为一种计算模型进行讨论. 我们将从描述一个“增强“版本的λ演算开始, 它包含一些“冗余特性“, 但更易于理解. 我们将首先展示增强λ演算在计算能力上如何等价于图灵机. 然后, 我们将展示如何将“增强λ演算“的所有特性实现为“纯“(即非增强)λ演算之上的“语法糖“. 因此, 纯λ演算在计算能力上等价于图灵机(因此也等价于RAM机器和其他所有图灵等价模型).
增强λ演算包括以下对象和操作:
- 布尔常量和IF函数: 存在λ表达式 和 满足以下条件: 对于每个λ表达式和 且 也就是说, 是一个函数, 接受三个参数 当时输出 当时输出
- 二元组: 存在一个λ表达式 我们将其视为配对函数. 对于每个λ表达式 是二元对 其中是其第一个成员, 是其第二个成员. 我们还有λ表达式和 分别提取二元组的第一个和第二个成员. 因此, 对于每个λ表达式 且 (在Lisp中, 和函数传统上称为
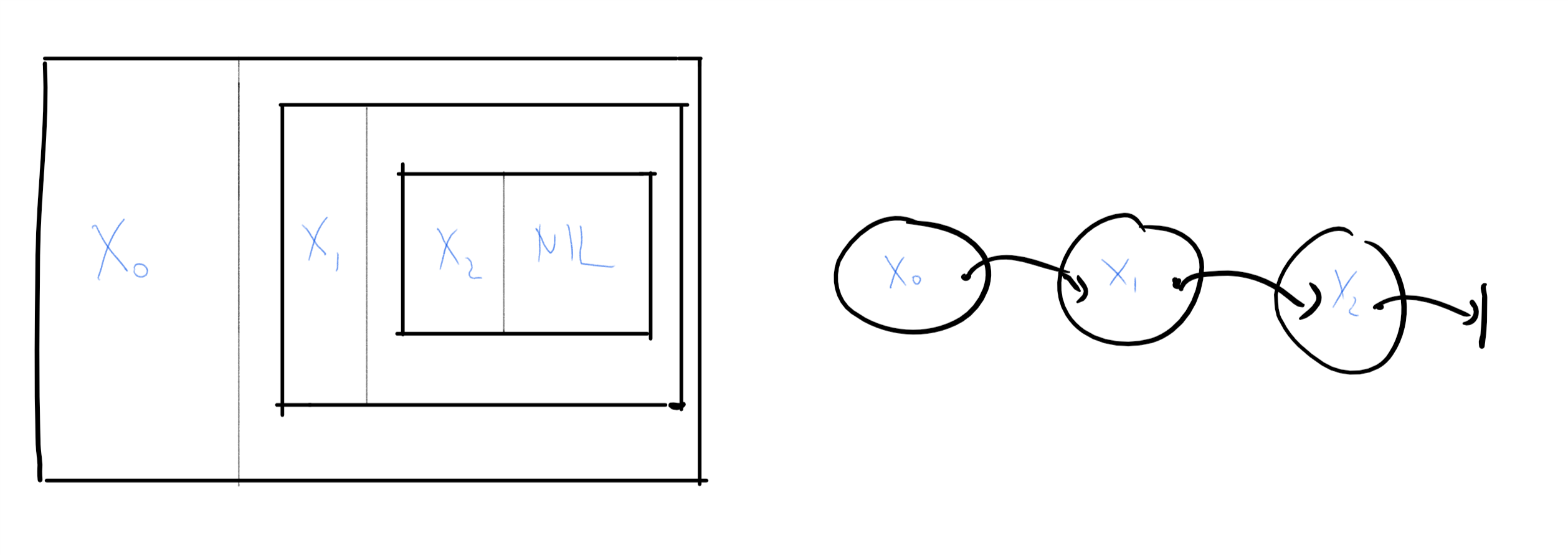
cons,car和cdr) - 列表和字符串: 存在λ表达式 对应空列表, 我们也用 表示. 使用和 我们可以构造列表. 思路是, 如果是一个元素列表, 形式为 那么对于每个λ表达式 我们可以使用表达式获得元素列表 例如, 对于任意三个λ表达式 以下对应三元素列表
λ表达式在上返回 在其他任何列表上返回 字符串就是由比特组成的列表.
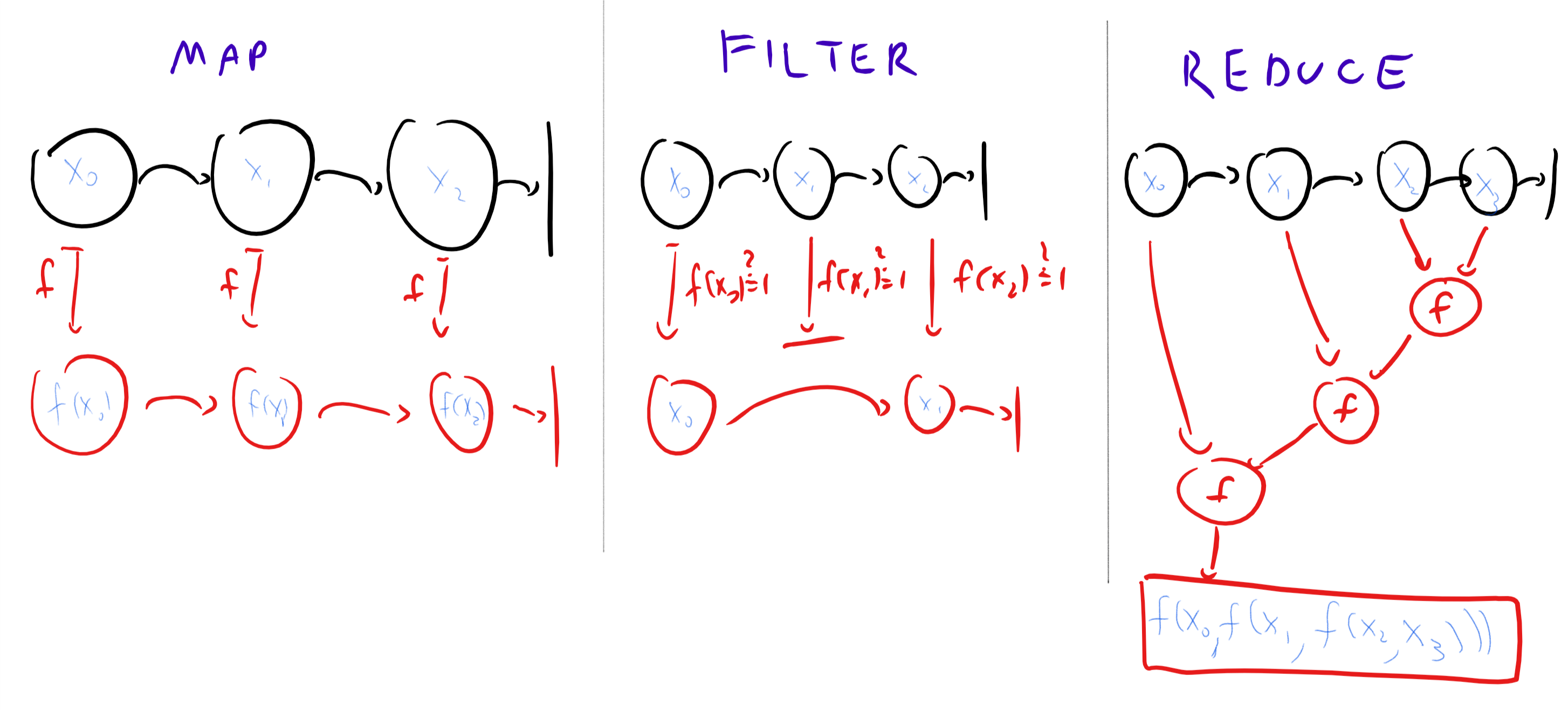
- 列表操作: 增强λ演算还包含列表处理函数 和 给定列表和函数 将应用于列表的每个成员, 得到新列表 给定列表和输出为或的表达式 返回列表 包含所有输出的的元素. 函数对列表应用“组合“操作. 例如, 将返回列表中所有元素的和. 更一般地, 接受列表 操作(我们视其为接受两个参数)和λ表达式(我们视其为操作的“中性元“, 例如加法为 乘法为 输出通过以下方式定义:
关于三个列表操作操作的图示, 请参见图 8.16.
- 递归: 最后, 我们希望能够执行递归函数. 由于在λ演算中函数是匿名的, 我们不能编写形式为 的定义, 其中包含对的调用. 相反, 我们使用函数 它接受一个额外输入作为参数. 运算符将接受这样的函数作为输入, 并返回的“递归版本“, 其中所有对的调用都替换为对此函数的递归调用. 也就是说, 如果我们有一个函数 接受两个参数和 那么将是函数 接受一个参数 使得对于每个
对练习 8.3的解答
对练习 8.3的解答
的等于 除非 因此
对练习 8.4的解答
对练习 8.4的解答
8.6.1 增强λ演算中的函数计算
一个增强λ表达式是通过将上述对象与应用和抽象规则组合而得到的. 简化λ表达式的结果是一个与远表达式等价的表达式, 因此如果两个表达式具有相同的简化结果, 则它们是等价的.
8.6.2 增强λ演算的图灵完备性
增强λ演算的基本操作或多或少相当于Lisp或Scheme编程语言. 鉴于这一点, 增强λ演算与图灵机等效或许并不令人惊讶:
定理 8.4的证明思路
定理 8.4的证明思路
为了证明该定理,我们需要证明 (1): 如果可由λ表达式计算, 则它可由图灵机计算, 以及 (2): 如果可由图灵机计算,则它可由增强λ表达式计算.
证明 (1) 相当直接.将简化规则应用于λ表达式基本上相当于“搜索和替换“,我们可以轻松地在NAND-RAM或Python中实现(两者在能力上都等价于图灵机). 证明 (2) 本质上相当于在函数式编程语言(如LISP或Scheme)中模拟图灵机(或编写NAND-TM解释器). 我们在下面给出细节, 但如何做到这一点是掌握一些本身就有用的函数式编程技术的良好练习.
定理 8.4的证明
定理 8.4的证明
我们仅给出证明的一个概述. “if“方向是简单的. 如上所述, 对λ表达式进行求值基本上相当于“搜索和替换”. 在命令式语言(如Python或C)中实现所有上述基本操作也是一个相当直接的编程练习, 并且使用相同的想法, 我们也可以在NAND-RAM中实现, 然后我们可以将其转换为NAND-TM程序.
对于“only if“方向,我们需要使用λ表达式模拟图灵机. 我们将通过首先为每个图灵机展示一个λ表达式来计算状态转移函数来实现这一点,该函数将的一个格局映射到下一个格局(见第8.4.2节).
的一个格局是一个字符串 其中是一个有限集合. 我们可以用有限字符串对每个符号进行编码, 因此我们将在λ演算中将格局编码为一个列表 其中是一个长度为的字符串(即一个由和组成的长度为的列表), 编码中的一个符号.
根据引理 8.1, 对于每个 等于 其中是某个有限函数. 使用我们对的编码 我们也可以将视为映射 到 通过练习 8.3,我们可以计算函数, 因此使用λ演算可以计算每个有限函数, 包括 利用这一见解, 我们可以使用λ演算计算如下. 给定一个编码格局的列表 我们定义列表和 分别编码格局向右和向左移动一步后的版本. 下一个格局定义为 其中表示的第个元素. 这可以通过递归(使用增强λ演算的运算符)计算如下:
一旦我们可以计算 我们就可以使用以下递归模拟在输入上的执行. 定义为从格局初始化时的最终格局. 函数可以递归定义如下:
检查一个格局是否停机(即, 转移函数是否输出可以轻松在λ演算中实现, 因此我们可以使用来计算 如果我们让是在输入上的初始格局, 那么我们可以从得到输出 从而完成证明.
8.7 从增强λ演算到纯λ演算
虽然我们所允许的增强型λ演算的“基本“函数集合比大多数Lisp方言提供的要小, 但从NAND-TM的角度来看, 它仍然显得有些“臃肿“. 我们能否用更少的函数来完成工作? 换句话说, 我们能否找到这些基本操作的一个子集, 使得该子集能够实现其余的操作?
事实上, 增强型λ演算的操作集合确实存在一个真子集, 可以用来实现其余所有操作. 这个子集就是空集.也就是说, 我们甚至可以不用和 仅使用λ运算符就能实现上述所有操作. 这完全是λ的天下!
这是一个很好的时机, 可以暂停一下, 思考你自己会如何实现这些操作. 例如, 可以先思考如何用来实现 然后如何结合与来实现 你也可以基于来实现 和 最具挑战性的部分是仅使用纯λ演算的操作来实现
定理 8.5背后的思想是, 我们将和本身编码为λ表达式, 并以此为基础进行构建. 这被称为Church编码(Church encoding), 因为它源于邱奇为了证明λ演算可以作为所有计算的基础所做的努力. 我们不会写出定理 8.5的完整形式化证明, 但会概述其中涉及的思想:
- 我们将定义为接受两个输入并输出的函数, 将定义为接受两个输入并输出的函数. 我们使用柯里化来实现双参数函数的效果, 因此且 (这种表示方案是表示
false和true的常见惯例, 但也有很多其他同样可行的表示和的替代方案) - 上述实现使得函数的实现变得平凡: 就是 因为且 我们可以写成以达到 的效果.
- 为了编码一个二元组 我们将产生一个函数 该函数在其“内部“包含和 并且对于每个函数都满足 也就是说, 我们可以通过写来提取二元组的第一个元素, 通过写来提取第二个元素, 因此且
- 我们将定义为忽略其输入并始终输出的函数. 即 函数在给定输入时, 检查如果我们将应用于函数(该函数忽略其两个输入并始终输出时是否得到 对于每个形式为 的有效二元组, 而 形式化地,
8.7.1 列表处理
现在我们面临一个更大的障碍, 即如何在纯λ演算中实现 和 事实证明, 我们可以用构建和 用构建 例如, 等同于 其中是对输入和输出的操作. (我将其验证留给读者你作为一个(推荐的)练习)
我们可以递归地定义 通过令 并规定给定一个非空列表(我们可以将其视为一个二元组 因此, 我们可能会尝试为编写一个递归的λ表达式, 如下所示:
这里唯一的问题是λ演算没有递归的概念, 因此这是一个无效的定义. 但当然, 我们可以使用我们的运算符来解决这个问题. 我们将把对““的递归调用替换为对作为额外参数给定的函数的调用, 然后将应用于此. 因此 其中:
8.7.2 Y组合子: 不需要递归的递归
(8.9)表明为了实现 与我们需要在纯λ演算中实现运算符. 这就是我们现在要做的事情.
我们如何在不使用递归的情况下实现递归?我们将用一个简单的例子来说明这一点 - 函数. 如练习 8.4所示, 我们可以递归地写出列表的函数如下:
其中是两个比特上的异或操作. 在Python中, 我们会这样写:
def xor2(a,b): return 1-b if a else b
def head(L): return L[0]
def tail(L): return L[1:]
def xor(L): return xor2(head(L),xor(tail(L))) if L else 0
print(xor([0,1,1,0,0,1]))
# 1
现在, 我们如何消除这个递归调用? 主要思想是, 既然函数可以接受其他函数作为输入, 那么在Python(当然还有λ演算)中, 给函数自身作为输入是完全合法的. 因此, 我们的想法是尝试提出一个非递归函数tempxor, 它接受两个输入: 一个函数和一个列表, 并且使得tempxor(tempxor,L)会输出L的异或值!
我们的第一次尝试可能只是简单地用me替换递归调用. 让我们将这个函数定义为myxor
def myxor(me,L): return xor2(head(L),me(tail(L))) if L else 0
让我们测试一下:
myxor(myxor,[1,0,1])
如果你这样做,解释器会给出以下错误:
TypeError: myxor() missing 1 required positional argument
问题是myxor期望两个输入: 一个函数和一个列表. 而在调用me时, 我们只提供了一个列表. 为了纠正这一点, 我们修改调用, 同时提供函数本身:
def tempxor(me,L): return xor2(head(L),me(me,tail(L))) if L else 0
注意在tempxor的定义中对me(me,..)的调用: 给定一个函数me作为输入, tempxor实际上会以自身作为第一个输入来调用函数me. 如果我们现在测试一下, 会发现实际上得到了正确的结果!
tempxor(tempxor,[1,0,1])
# 0
tempxor(tempxor,[1,0,1,1])
# 1
因此, 我们可以将xor(L)简单地定义为return tempxor(tempxor,L).
上述方法不仅适用于XOR. 给定一个接受输入x的递归函数f, 我们可以获得一个非递归版本, 如下所示:
- 创建函数
myf, 它接受两个输入me和x,并将对f的递归调用替换为对me的调用. - 创建函数
tempf,它将myf中形式为me(x)的调用转换为形式为me(me,x)的调用. - 函数
f(x)将被定义为tempf(tempf,x).
以下是我们如何在Python中实现RECURSE运算符的方式. 它将接受一个如上所述的函数myf, 并将其替换为一个函数g, 使得对于每个x, g(x)=myf(g,x).
def RECURSE(myf):
def tempf(me,x): return myf(lambda y: me(me,y),x)
return lambda x: tempf(tempf,x)
xor = RECURSE(myxor)
print(xor([0,1,1,0,0,1]))
# 1
print(xor([1,1,0,0,1,1,1,1]))
# 0
从Python到λ演算: 在λ演算中, 一个接受两个输入的函数被写作 因此, 函数被简单地写作 类似地, 函数就是 (你明白为什么吗?) 因此, 上述定义的函数tempf可以写作λ me. myf(me me). 这意味着, 如果我们将RECURSE的输入记为 那么 其中 或者换句话说
在线附录包含一个使用Python实现的λ演算. 以下是该附录中递归XOR函数的实现: 3
# XOR of two bits
XOR2 = λ(a,b)(IF(a,IF(b,_0,_1),b))
# Recursive XOR with recursive calls replaced by m parameter
myXOR = λ(m,l)(IF(ISEMPTY(l),_0,XOR2(HEAD(l),m(TAIL(l)))))
# Recurse operator (aka Y combinator)
RECURSE = λf((λm(f(m*m)))(λm(f(m*m))))
# XOR function
XOR = RECURSE(myXOR)
#TESTING:
XOR(PAIR(_1,NIL)) # List [1]
# equals 1
XOR(PAIR(_1,PAIR(_0,PAIR(_1,NIL)))) # List [1,0,1]
# equals 0
上述运算符更广为人知的名字是Y组合子(Y combinator).
它是一族不动点算子(fixed point operators)中的一个, 给定一个λ表达式 找到的一个不动点(fixed point) 使得 如果你思考一下就会发现, 就是上述的不动点. 是这样的函数: 对于每个 如果将作为的第一个参数代入, 我们会得到 换句话说 因此, 为找到不动点等同于对其应用
8.8 Church-Turing论题(讨论)
[1934年], 丘奇一直在思索, 并最终明确提出了λ可定义函数就是所有能行可计算函数的观点….当丘奇提出这一论点时, 我坐下来试图反驳它….但很快意识到[我的方法失败了], 一夜之间我成了该论点的支持者.
——斯蒂芬·克林,1979年.
我们定义了一个函数是可计算的, 如果它可以通过NAND-TM程序进行计算, 并且我们已经看到, 如果我们将NAND-TM程序替换为Python程序, 图灵机, λ演算, 元胞自动机以及许多其他计算模型, 该定义将保持不变. Church-Turing论题指出, 这是“可计算“函数的唯一合理定义. 与我们之前看到的“物理扩展Church-Turing论题“(PECTT)不同, Church-Turing论题并未做出可以通过实验检验的具体物理预测, 但它确实激励了诸如PECTT之类的预测. 我们可以将Church-Turing论题视为一种定义选择的提倡, 对所有潜在计算设备做出某种预测, 或者提出一些约束自然界的自然法则. 用Scott Aaronson的话来说, “无论它是什么, Church-Turing论题只能被视为极其成功”. 迄今为止, 尚无候选计算设备(包括量子计算机, 以及更不合理的模型, 例如我们之前提到的假设性“封闭时间曲线“计算机)对Church-Turing论题构成严肃挑战. 这些设备可能使某些计算更高效, 但并未改变有限可计算与不可计算之间的界限.(我们在第13.3节讨论的扩展Church-Turing论题规定, 图灵机也捕获了可高效计算内容的极限. 正如其物理版本所言, 量子计算对这一论题构成了主要挑战)
8.8.1 不同的计算模型
我们可以将我们已经看到的模型总结在以下表格中:
| 计算问题 | 模型类型 | 示例 |
|---|---|---|
| 有限函数 | 非均匀计算 (算法依赖于输入长度) | 布尔电路, NAND电路, 直线程序 (例如, NAND-CIRC) |
| 具有无界输入的函数 | 顺序访问内存 | 图灵机, NAND-TM程序 |
| – | 索引访问 / RAM | RAM机, NAND-RAM, 现代编程语言 |
| – | 其他 | λ演算, 细胞自动机 |
用于计算有限函数和任意输入长度函数的不同模型.
在第17章中, 我们将研究_内存受限_计算. 事实证明, 具有常量内存的NAND-TM程序等价于有限自动机(finite automata)模型(有时也会加上“确定性“或“非确定性“的形容词, 该模型也被称为有限状态机(finite state machines)), 它又捕获了正则语言(regular language)的概念(那些可以用正则表达式描述的语言), 这是我们将在第10章中看到的概念.
- 虽然我们使用图灵机定义了可计算函数, 但我们同样可以使用许多其他模型来定义, 不仅包括NAND-TM程序, 还包括RAM机, NAND-RAM, λ演算, 细胞自动机和许多其他模型.
- 非常简单的模型也可以是“图灵完备“的, 即它们可以模拟任意复杂的计算.
8.9 习题
令为以下函数. 输入是一个二元组 其中 是一个由键值对组成的列表的编码, 其中是二进制字符串. 输出是满足的最小对应的(如果这样的存在), 否则输出空字符串.
- 证明可由图灵机计算.
- 令为一个函数, 其输入是一个对组成的列表 其输出是通过将对添加到的开头而得到的列表 证明可由图灵机计算.
- 假设我们用一个键/值对的列表来编码一个NAND-RAM程序的配置, 其中键要么是标量变量名
foo, 要么是形如Bar[<num>]的形式(其中<num>是某个数字), 并且它包含所有非零的变量值. 令为一个函数, 它将NAND-RAM程序在某一时刻的配置映射到下一时刻的配置. 证明可由图灵机计算(你不需要实现每一个算术操作: 实现加法和乘法就足够了). - 证明对于每个可由NAND-RAM程序计算的函数 也可由图灵机计算.
令为一个函数, 其在输入一个编码三元组的字符串时, 如果和在中不连通, 则输出一个编码的字符串; 否则输出一个编码从到的最短路径长度的字符串. 证明可由图灵机计算. 参见脚注中的提示. 4
令为一个函数, 其在输入一个编码三元组的字符串时, 如果和在中不连通, 则输出一个编码的字符串; 否则输出一个编码从到的最长简单路径长度的字符串. 证明可由图灵机计算. 参见脚注中的提示. 5
证明对于每个不含自由变量的λ表达式 存在一个等价的λ表达式 该表达式仅使用变量 和 6
- 令 证明如果我们使用按名调用求值顺序, 则的简化过程会在确定的步数内结束; 而如果我们使用按值调用顺序, 则它永远不会结束.
- (加分, 挑战性)令为任意λ表达式. 证明如果使用按值调用顺序时简化过程会在确定的步数内结束, 那么使用按名调用顺序时它也会在确定的步数内结束. 参见脚注中的提示. 7
给出一个增强的λ演算表达式来计算函数 该函数在输入一对相同长度的列表和时, 输出一个由个对组成的列表 使得的第个元素(我们记为是对 因此将这两个元素列表“压缩“成一个由对组成的单个列表. 8
习题 8.12 (λ演算到NAND-TM编译器(挑战性)).
用你选择的编程语言给出一个程序, 该程序将λ表达式作为输入, 并输出一个NAND-TM程序 该程序计算与相同的函数. 为了部分得分, 你可以在输出程序中使用GOTO和所有NAND-CIRC语法糖. 你可以使用任何对你方便的λ表达式到二进制字符串的编码. 参见脚注中的提示. 10
这个问题将帮助你更好地理解图灵机状态转移函数的局部性概念. 这种局部性在诸如λ演算和一维元胞自动机的图灵完备性等结果中起着重要作用, 也出现在我们将在本课程后面看到的Godel不完备定理和Cook Levin定理等结果中. 定义STRINGS为具有以下语义的编程语言:
- 一个
STRINGS程序有一个单一的字符串变量str, 它既是的输入也是输出. 该程序没有循环也没有其他变量, 而是由一系列修改str的条件搜索和替换操作组成. STRINGS程序的操作包括:REPLACE(pattern1,pattern2), 其中pattern1和pattern2是固定字符串. 这将str中第一次出现的pattern1替换为pattern2.if search(pattern) { code }: 如果pattern是str的子串, 则执行code. 代码code本身可以包含嵌套的if语句. (也可以添加else { ... }来在pattern不是str的子串时执行).- 返回值是
str.
- 一个
STRINGS程序计算一个函数 如果对于每个 我们将str初始化为然后执行中的指令序列, 则在执行结束时str等于
例如, 以下是一个STRINGS程序, 它计算函数 使得对于每个 如果包含一个形如的子串, 其中 则 其中是通过将中第一次出现的替换为得到的.
if search('110011') {
replace('110011','00')
} else if search('110111') {
replace('110111','00')
} else if search('111011') {
replace('111011','00')
} else if search('111111') {
replace('1111111','00')
}
证明对于每个图灵机程序 存在一个STRINGS程序 它计算函数, 该函数将每个编码的有效配置的字符串映射到编码计算下一步的配置的字符串. (我们不关心该函数在那些不编码有效配置的字符串上的行为)你不必完整地写出STRINGS程序, 但你需要给出一个令人信服的论证, 证明这样的程序存在.
8.10 参考文献
Moore和Mertens的杰出著作(Moore, Mertens, 2011)第七章对这部分内容进行了精彩阐述.
RAM模型在研究实用算法的具体复杂度时非常有效, 其理论研究始于Cook和Reckhow(Cook, Reckhow, 1973). 不过需要注意的是, 不同文献和场景中对RAM模型允许的操作集及其成本定义存在差异. 正如Shamir(Shamir, 1979)已指出的, 在定义时需要特别谨慎——尤其是在字长可变的情况下. Savage著作(Savage, 1998)第三章给出了RAM机更形式化的描述, 亦可参阅Hagerup的论文(Hagerup, 1998). 关于不依赖输入规模的RAM算法研究(即transdichotomous RAM model)则由Fredman和Willard(Fredman, Willard, 1993)开创.
目前讨论的计算模型本质上是串行的, 但当今大量计算已转向并行模式——无论是通过多核处理器, 还是通过数据中心或互联网的大规模分布式计算. 虽然并行计算在实践中至关重要, 但对于“可计算与不可计算“的界限问题并未产生本质影响. 毕竟, 若计算任务可由台机器在时间内完成, 那么单台机器只需时间同样可以完成.
λ演算由Church(Church, 1941)提出. Pierce的专著(Pierce, 2002)是该领域权威教材, 另可参考Barendregt的著作(Barendregt, 1984). “柯里化“以逻辑学家Haskell Curry命名(Haskell编程语言同样得名于他). Curry本人认为这一概念应归功于Moses Schönfinkel, 但出于某种原因, “Schönfinkeling“这一术语始终未能流行.
与大多数编程语言不同, 纯λ演算不包含类型概念. 其中的每个对象既可视为λ表达式, 也可作为接收单参数并返回单值的函数. 所有函数均采用“搜索替换“机制:当传入非常规参数时, 系统会将形参全部替换为输入表达式的副本. λ演算的类型化变种已成为研究热点, 与编程语言类型系统及计算机可验证证明系统紧密关联(参见Pierce, 2002). 部分类型化λ演算变种摒弃了无限循环特性, 这使其成为程序静态分析和机器验证证明的重要工具, 我们将在第10章和第22章重新探讨这一主题.
陶哲轩曾提出通过证明流体动力学(“水计算机”)的图灵完备性来解决Navier-Stokes方程行为问题, 相关科普论述可参阅此文.
1: 一些编程语言可以访问的内存量有固定的(即使非常大)上限, 这正式地阻止了它们适用于计算无限函数并因此模拟图灵机. 我们在本次讨论中忽略此类问题, 并假定可以访问某种容量没有固定上限的存储设备.
2: 译者注: 在本翻译版中会使用中文
3: 由于Python语法的特定问题, 在此实现中, 我们使用f * g表示将f应用于g,而不是f g, 并使用λx(exp)而不是λx.exp进行抽象. 我们还使用_0和_1表示和的λ项, 以免与Python常量混淆.
4: 你不需要给出图灵机的完整描述:使用我们的“鱼与熊掌兼得“范式, 通过论证更强大的等价模型来证明这种机器的存在.
5: 与习题 8.4相同的提示. 注意, 为了证明是可计算的, 你不必给出一个高效的算法.
6: 提示: 你可以通过“将它们配对“来减少函数所使用的变量数量. 也就是说, 定义一个λ表达式 使得对于每个 是某个函数 满足且 然后使用迭代地减少所使用的变量数量.
7: 对表达式的结构使用归纳法.
8: 是这个操作的常用名称, 例如在Python中. 不要将其与zip压缩文件格式混淆.
9: 使用和(以及可能的 你可能还会发现习题 8.10中的函数有用.
10: 尝试建立这样一个过程: 如果数组Left包含λ表达式的编码, 并且数组Right包含另一个λ表达式的编码, 那么数组Result将包含