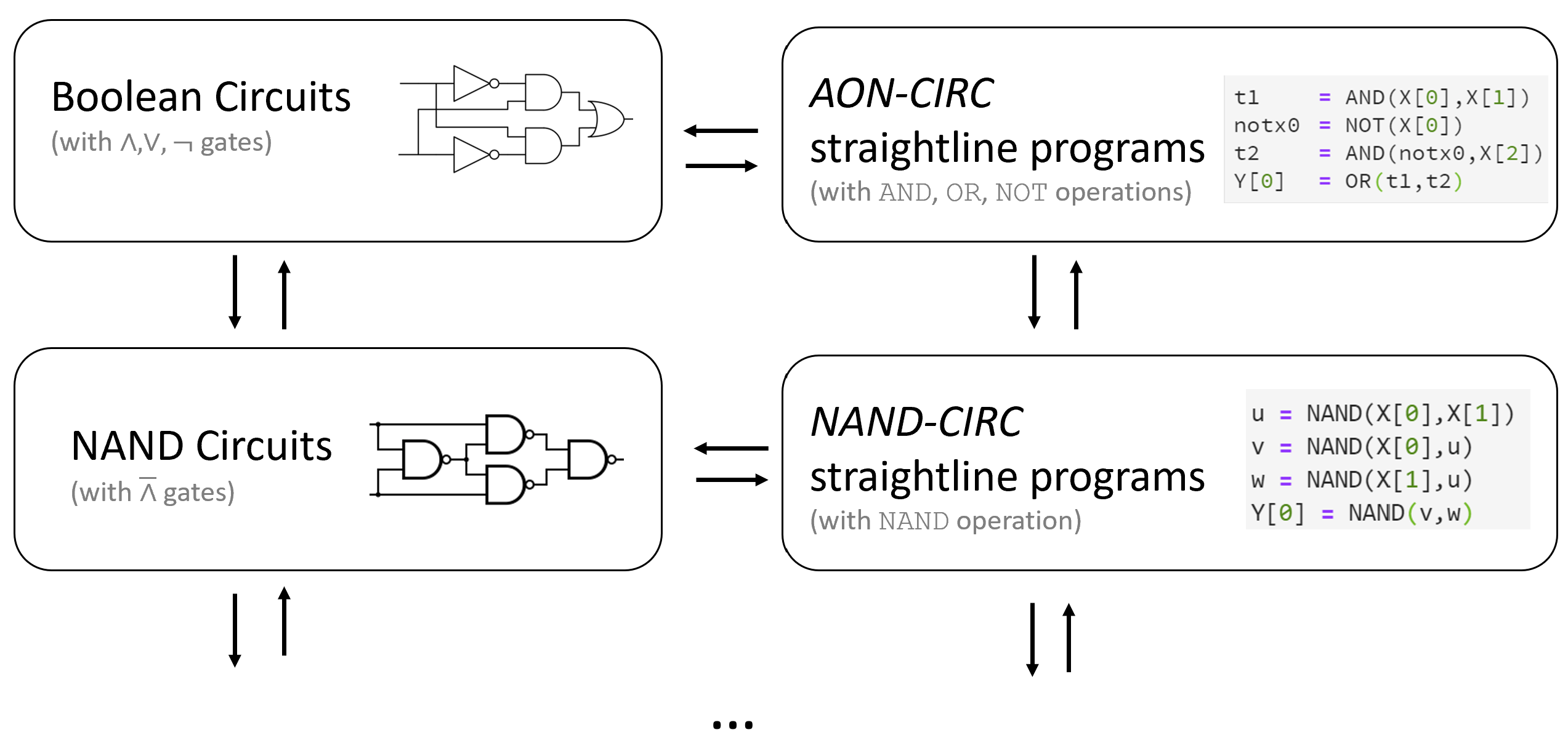
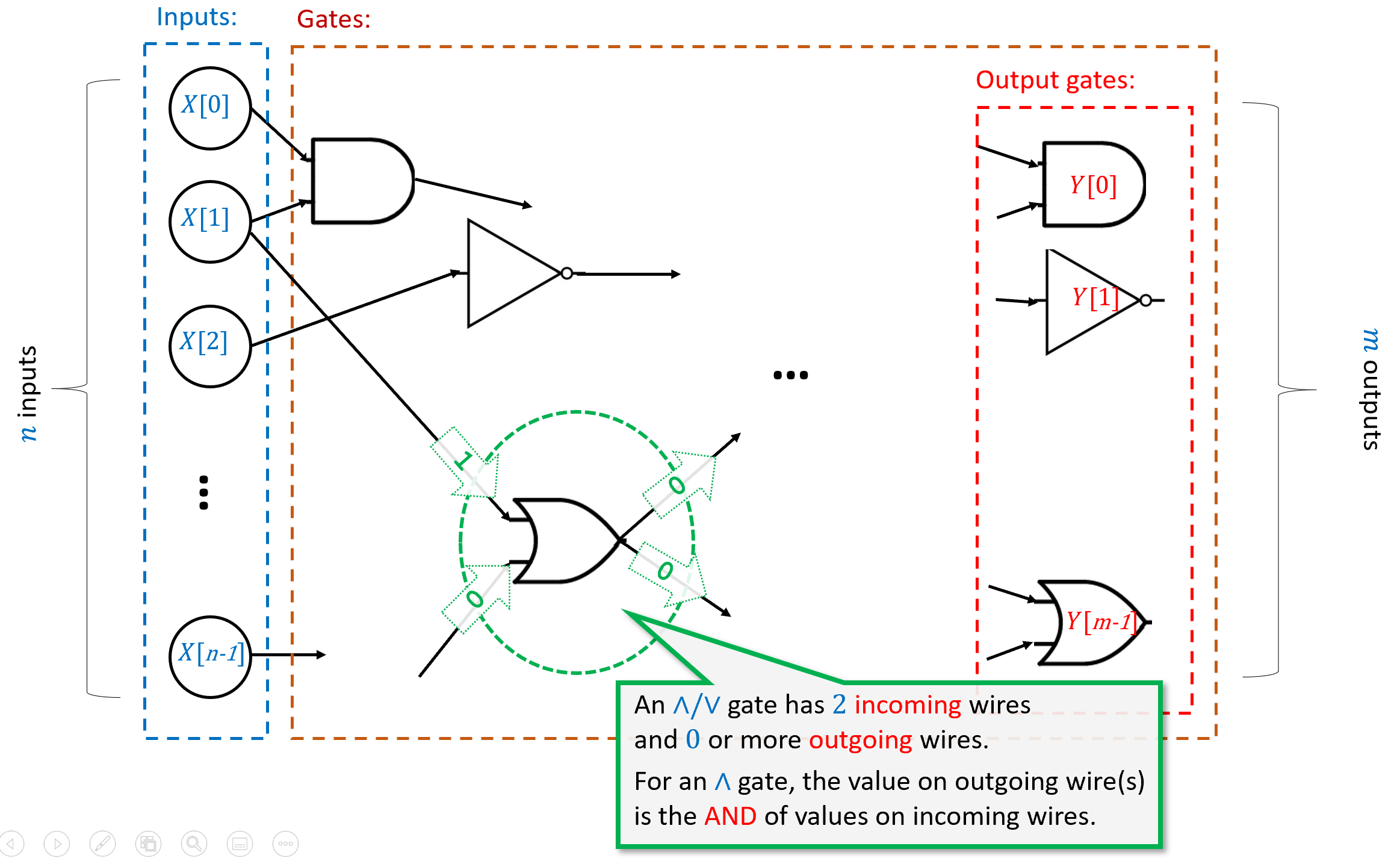
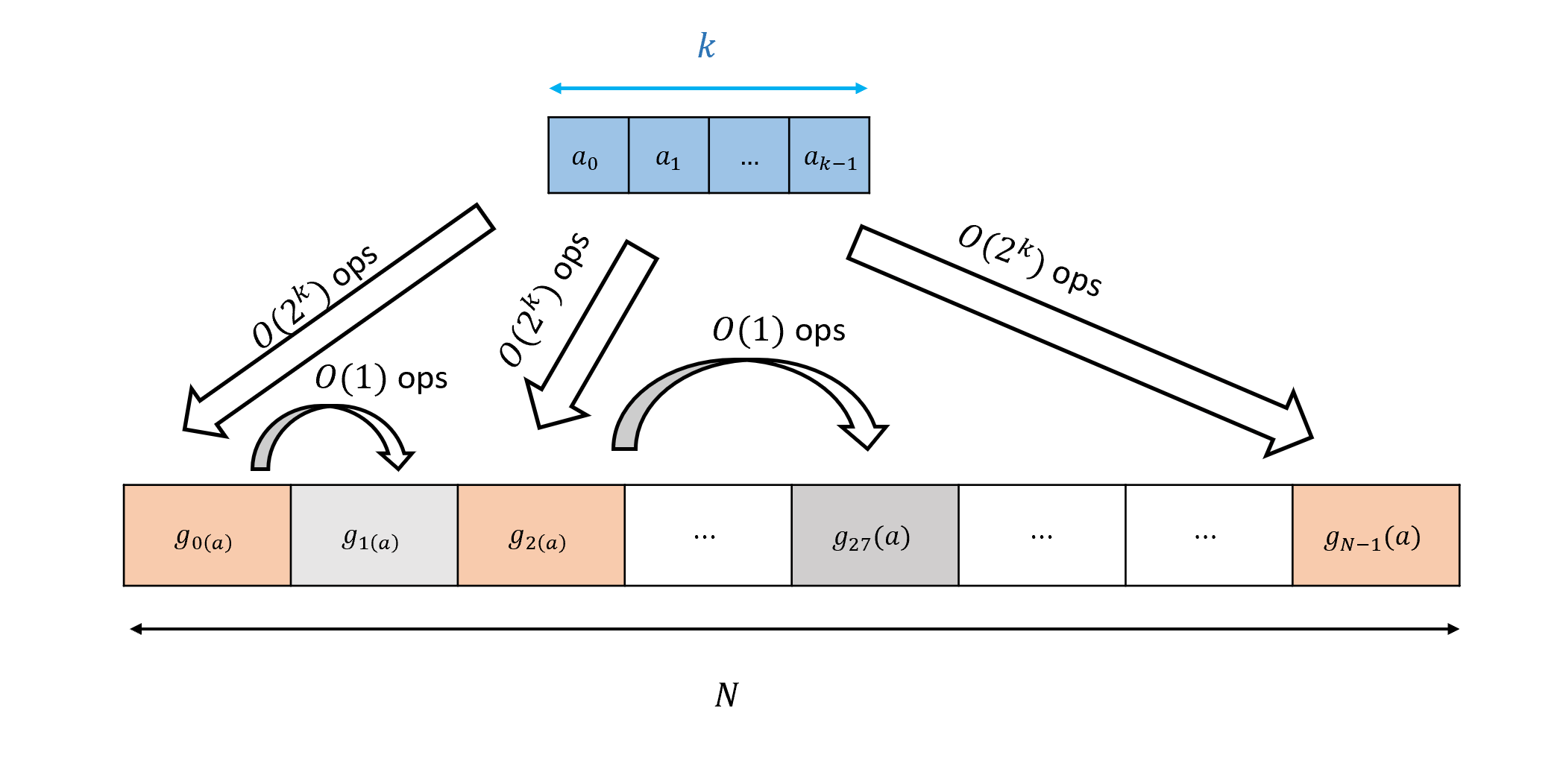
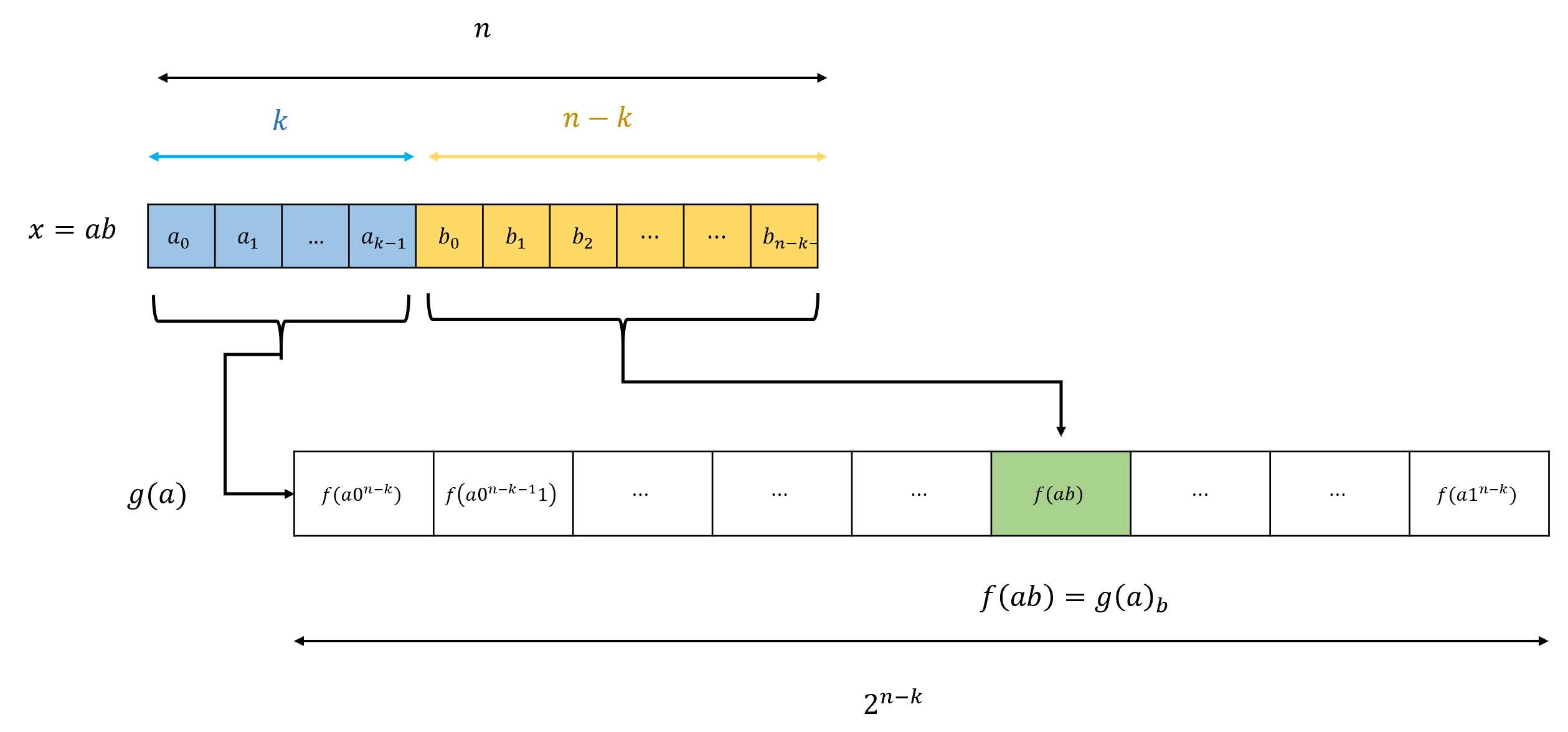
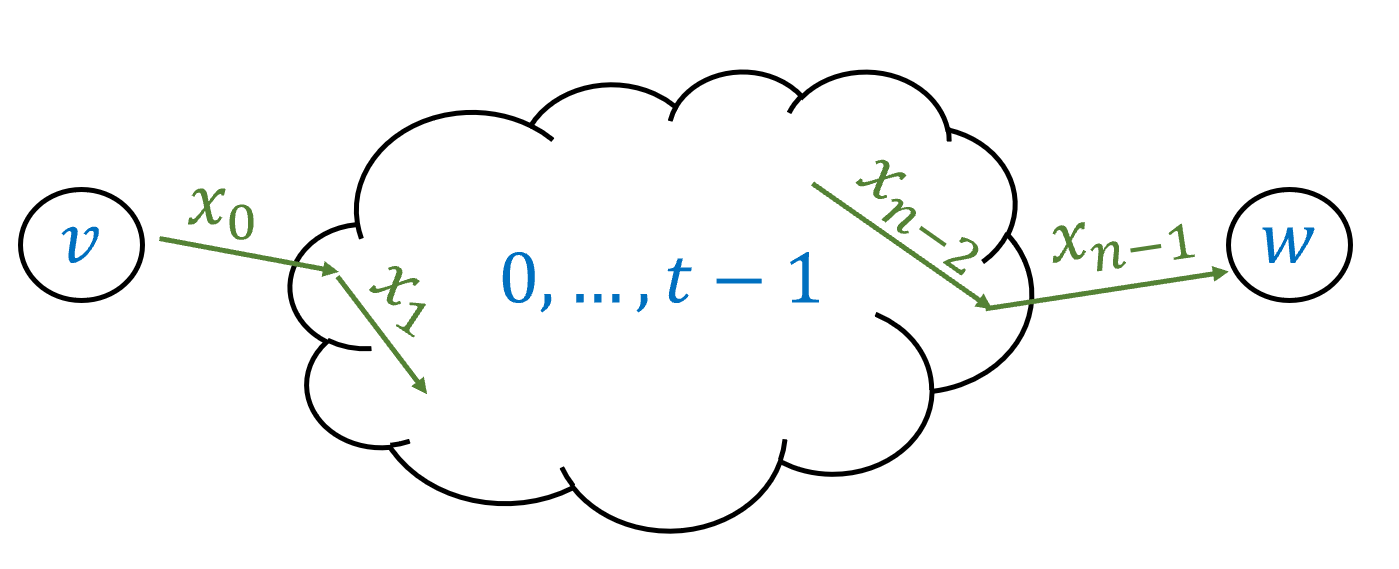前言
我们珍视但无法许诺自己能够达成这样的理想:我们对于“无用的知识”无拘无束的追求,将会在未来如同以往一样结出硕果。…… 一所能够解放人类灵魂的机构,无论其毕业生是否作出所谓“有用”的贡献,其正当性就已经得到保证。一首诗歌、一首交响曲、一幅画卷、一条数学真理、一个科学事实,它们自身就已经包含了大学、学院以及研究所科学研究中需要或者要求的所有正当性。 ——Abraham Flexner,《无用以为用》
我建议你尝试你力所能及最困难的课程,因为只有当你挑战自我的时候才能够学到最多的知识……另外,我觉得CS121这门课真的很难。 ——Mark Zukerberg,2005
这本书是针对本科生的计算理论入门课程。本课程的课程目标如下:
- 学生们能够了解,计算在任何自然或者人造的系统中都存在,不仅仅存在于硅基现代计算机当中;
- 类似地,我们要超越将计算理解为极其重要的“工具”的观念,进一步认识到——计算是描述自然、物理、数学甚至社会学概念的洞察工具;
- 学生们能够了解“普遍性”的观念以及编码和数据的对偶性观念;
- 学生们应该了解如何从数学上定义计算,并使用这样的工具去证明(有时仅仅是猜想)计算的下界以及不可能的结果。
- 学生们要了解一些在现代理论计算机科学中出人意料的结果和发现,包含NP完全性的普遍性、交互的力量、随机性以及去随机的力量、用计算“难度”保证优质的加密,以及量子计算的无限可能。
我希望通过上述课程,学生们能够认识到计算的能力与隐患。这是因为,在许多不同的背景下,例如宏定义和脚本等等看似“静态”和“有限制”的内容与形式,我们都需要讨论“计算”在其中表现出的性质。学生们应该能够理清计算证明的逻辑,包含归约的核心观点以及“自引用”的证明(例如对角化证明中,我们通过将其自身编码作为输入以导出矛盾)。学生们应该明白,某些问题是固有的难解决的,同时他们也应该能够在面对一个新问题的时候,识别其是否难以解决。尽管本书仅仅是短浅地涉猎密码学,学生们也应该了解我们在密码学中使用计算难度的目的。不论如何,本书不会局限于特定的技巧,而是要让学生们具有一种全新的思维——将计算本身视为独立的对象来审视与探究,并展示这种思维如何带来深远洞见与广泛应用。
我写作本书的目标是以最简单的方式阐明计算理论中的概念,并且尝试让规范的记号与模型的核心理念更加好理解而不是晦涩难懂。我同时尝试利用学生们在编程方面的经验,拉近学生们与计算理论之间的关系(至少让教学内容更加有趣!),因此我使用了(高度简化)的编程语言来描述我们的计算模型。话虽如此,本书并不假定你对于任何特定编程语言驾轻就熟,而只要求你对“编程”这一总体概念有基本的熟悉。我们常常使用编程中的一些比喻和习惯,偶尔会提及Python、C或者Lisp等具体语言,但即使对于这些语言不熟悉,学生们也能毫无障碍地理解相关描述。
本书中的证明,包含通用图灵机的存在性、有限值函数的电路可计算性、Cook-Levin定理以及其它许许多多的定理,通常都是构造性和算法性的,因为他们的最终目的都是将一个程序转换为另一个程序。尽管不看代码就阅读证明是完全可能的,我坚信保留代码资源,并且在各实际问题上实现它们并观察其表现对于学生具体地理解定理内容是更加有效的。为了达到这个目的,我们搭建了一个辅助的网站(仍在开发中)以允许学生们在我们定义的不同的计算模型上运行这些程序。与此同时,本网站也可以观看某些定理的构造性证明。
前言1 致学生们
这一本书可能相当具有挑战性,主要原因是这本书中将各种计算理论的观点和技术融合到了一起。其中一些技巧是比较难以掌握的,不论是通过对角线论证证明停机问题的不可判定性,还是在NP完全问题归约中使用的组合工具,抑或是分析概率算法,再或者是通过讨论对抗过程从而证明密码学基本构件的安全性。
阅读这本书的最佳方法是积极地去阅读笔记,所以说我建议你准备好你的笔。当你阅读这本书的时候,我鼓励你不时地停下来并思考如下地问题:
- 当我陈述一个定理的时候,停下来并用一点时间尝试在你阅读证明之前自己证明这个定理。在这短短五分钟的尝试以后,你将会为能更好地理解标准证明而感到惊喜。
- 当你在阅读定义的时候,一定要保证你完全理解了定义的含义,以及哪些自然的例子能够成为定义所描述的对象。此外,一定要去思考定义背后的动机,以及是否有其它自然的方式来形式化这些概念。
- 积极地注意你阅读过程中,脑中浮现出的问题,并且考虑他们是否在阅读文本的过程中得到了解答。
一个普遍的规则是,理解定义比理解定理更加重要,理解定理比理解证明更加重要。不论如何,在你证明定理之前,你一定要理解它到底陈述的是什么,一定要了解定理中对象所涉及的定义。不论证明如何复杂,我会提供证明定理的“证明想法”。你可以在第一次阅读的时候自由地跳过正式的证明,而单独把注意力放在“证明想法”上面。
本书包含了一部分代码片段,但这并不代表他们是编程文本。实际上,在阅读本书的时候,你不必知道如何进行编程。我们使用代码的原因,仅仅是为了更加精确地描述计算过程。实际的实现细节对于我们而言是不重要的,因此我们将会强调以更多考量换取代码可读性的重要性,例如错误处理、代码封装,等等,这些技巧对于我们实际的编程是非常重要的。
但是这些努力是否值得?
这并不是一本简单的书,你有理由思考自己为什么自己要花费这么多精力在学习这本书之上。一个对于计算理论课程的经典辩护是,你可能会在你未来的工作中遇到这些概念。你可能会遇到一个非常困难的问题,而后续你会意识到它是一个NP完全问题;又或者,你会在未来找到应用你所学到的正则表达式的地方。这可能是实话,但是这本书的主要功用并不是教给你任何实用的工具或者技能,而是给予你一种全新的思考方式:一种在计算问题出现时、穿破重重看似无关的设定识别它们的思想,一种建模计算任务和问题的思想,以及通过以上两个思想进行推理的能力。
无论你如何运用这本书,我都相信学习这本书是非常重要的。这是因为,它包含了许多非常优美且基本的概念。在本世纪,计算与信息扮演了能量和物质在上世纪的角色——作为我们理解世界的基石,而并不仅仅是作为我们科技和经济的工具。这本书将会让你简单了解这些理论背后的内容,并且希望能够激发各位读者进一步学习和了解更多知识的动力。
前言 2 致未来的授课教师们
这本书虽然是我为哈佛大学课程所作,但是我希望其它授课教师也认为它大有裨益。从某种意义上来讲,它与卡内基梅隆大学和麻省理工学院开设的“计算理论导论”和“伟大的想法”等课程的内容是类似的。
这本书所使用的教学方法与其它传统书籍(例如Hopcroft和Ullman于1969年出版的教材以及Sipser在1997年出版的教材)最显著的不同,在于本书将不会从有限自动机开始建立计算模型。相反,我们将会从布尔电路出发来建立这一切。我们相信,布尔电路才是计算理论中比自动机更加基本的内容。(甚至也是更加实用的!)更重要的是,布尔电路是许多只会在介绍现代理论计算机理论的课程中才会被提及的诸概念的前置概念。这些理论理论包括现代密码学、量子计算、去随机化理论、一些对于证明的尝试,等等等等。甚至,在某些并不必须使用布尔电路的情况下,布尔电路能够极大地简化这些问题(例如在证明Cook-Levin定理时)。
不仅如此,我认为以布尔电路而不是有限自动机作为起始,还有许多教学上的理由。布尔电路是更加自然的计算模型,其与硅基电路联系紧密,能够与学生们的实践直接产生关联。按理来说,有限值函数往往比无限值函数更容易掌握,因为我们完全可以将它的真值表直接写出。“任何一个有限值函数都可以被布尔函数计算”,这样的简单但是重要的定理可以作为课程的一个极好的起点。更进一步,许多计算理论中的观点,例如编码和数据之间对偶关系的观点、“普遍性”的观点等等,我们都可以从这一理论中体悟出来。
紧随布尔电路,我们将会进入图灵机的学习,并且证明一些重要的结果,例如通用图灵机的存在、停机问题的不可计算性以及Rice’s Theorem。我们将会在了解图灵机和不可判定性之后讨论自动机,并将其作为限制型计算模型的例子(这一类机器的停机问题可以被高效解决)。
尽管按照电路——图灵机——自动机的顺序来介绍并不是我们的初衷,这个顺序与这些模型的发现的时间顺序是恰好吻合的。布尔代数可以追溯到Boole和DeMorgan在19世纪40年代的工作(尽管布尔电路的严格定义由Shannon在90年之后才给出)。Alan Turing在20世纪30年代定义了我们现在所称呼的“图灵机”,而有限自动机在1943年才在McCulloch和Pitts的工作中被正式提出。并且,直到1959年Rabin和Scott发表了他们重要的工作以后,自动机才逐渐被人们所了解。
更重要的是,尽管诸如有限自动机、正则表达式以及上下文无关语法在工程中非常重要,这些模型能够得到重用(不论是用于语法解析、分析生命周期和安全性还是用于软件定义路由表)绝大部分都要归因于他们是可控制的模型,我们可以轻易地通过它们来回答一些语义上的问题。在学生了解了通用计算模型的语义性质的不可判定性,它们可能会对这些实际应用上的想法感到叹为观止。
从电路入门使得我们证明Cook-Levin Theorem非常方便。事实上,我们的证明可以被一些Python程序完成。通过将这个证明与标准的归约结合,学生们能够直观地欣赏计算理论中的问题是如何被转化为图中独立集的存在性问题的。
这里,我们列举出一些与过往文献的不同:
-
为了衡量时间复杂度,我们使用在算法课中使用过的标准的RAM机器模型(隐式的)而不是图灵机。尽管这两个模型毫无疑问是多项式等价的,且两个模型上复杂度类和以及没有任何区别,我们的选择使得记号和之间的区别更加有意义。这样的选择使得这些更加细致的复杂度类型对应上学生们在算法课上学到的关于线性和二次时间的非正式定义(或者是对于需要他们手写代码的面试环节有所好处)(译者注:面试环节通常需要面试者在白板上手写代码,并给出时间复杂度分析)。
-
我们使用“函数”而不是“语言”。这就是说,与其说“图灵机判定语言”,我们说它“计算了一个布尔函数”(译者注:表示任意长度的二进制串,或者说0-1串)。“语言”这一术语兴起于Chomsky的1956年的工作,但是往往令人迷惑。“语言”相关的术语同时也使得讨论有关计算有多比特输出的函数的算法相关的概念非常的低效(包含一些非常基本的任务,例如讨论加法、乘法,等等)。但是,使用函数而不是语言意味着我们必须格外警惕学生可能会把“计算任务的规范”(函数)和“该任务的实现”(程序)搞混。另一方面,我们必须重复向学生强调和并训练他们要牢记这一点,无论使用何种记号。但是与此同时,本书同样会时不时提及“语言”相关的术语,以便于学生在课外查找相关资料。
上面教学大纲对于有限自动机和上下文无关语言的减免使得授课教师们能够讲授更多在现代理论课程之前所需要了解的知识。它们包括:随机性和计算,程序和证明之间的交互(包含哥德尔不完备定理、交互式证明系统、甚至包含一些Lambda演算、Curry-Howard同构)、密码学以及量子计算。
这本书提供了足以进行自学的细节。为了达到这个目的,每一个章节的开头都会列举这个章节的学习目标,末尾则会进行总结和回顾,行文之间穿插着“停顿框”以鼓励学生们停下来并求解一个问题或者检查他们是否在继续学习之前完全明白了前文所述的定义。
“第0章”的第五节提供了本书的一个“地图”,概括性地描述了不同章节的大概内容,同时还阐述了他们之间的依赖关系。这对于课程的规划是非常有益的。
致谢
这段文字正在持续更新,我收到了许多人的反馈,对此我深怀感激。Salil Vadhan 与我共同教授了这门课程的最初版本,在此过程中给予了我大量宝贵的反馈与洞见。Michele Amoretti 和 Marika Swanberg 仔细审阅了本书的若干章节,并提供了极其详尽且有益的评论。Dave Evans 和 Richard Xu 提交了许多 pull request,修正错误并改进措辞。感谢 Anil Ada、Venkat Guruswami 和 Ryan O’Donnell 分享他们在教授 CMU 15-251 时的经验与建议。感谢 Adam Hesterberg 和 Madhu Sudan 就使用本书教授 CS 121 的经验提出意见。Kunal Marwaha 提供了诸多评论,并在本书的技术制作方面给予了极大帮助。
感谢所有通过 GitHub 仓库 https://github.com/boazbk/tcs 发送评论、报告错别字或提交 issue 与 pull request 的人。特别感谢以下人士的宝贵反馈:Scott Aaronson、Michele Amoretti、Aadi Bajpai、Marguerite Basta、Anindya Basu、Sam Benkelman、Jarosław Błasiok、Emily Chan、Christy Cheng、Michelle Chiang、Daniel Chiu、Chi-Ning Chou、Michael Colavita、Brenna Courtney、Rodrigo Daboin Sanchez、Robert Darley Waddilove、Anlan Du、Juan Esteller、David Evans、Michael Fine、Simon Fischer、Leor Fishman、Zaymon Foulds-Cook、William Fu、Kent Furuie、Piotr Galuszka、Carolyn Ge、Jason Giroux、Mark Goldstein、Alexander Golovnev、Sayan Goswami、Maxwell Grozovsky、Michael Haak、Rebecca Hao、Lucia Hoerr、Joosep Hook、Austin Houck、Thomas Huet、Emily Jia、Serdar Kaçka、Chan Kang、Nina Katz-Christy、Vidak Kazic、Joe Kerrigan、Eddie Kohler、Estefania Lahera、Allison Lee、Benjamin Lee、Ondřej Lengál、Raymond Lin、Emma Ling、Alex Lombardi、Lisa Lu、Kai Ma、Aditya Mahadevan、Kunal Marwaha、Christian May、Josh Mehr、Jacob Meyerson、Leon Mlodzian、George Moe、Todd Morrill、Glenn Moss、Haley Mulligan、Hamish Nicholson、Owen Niles、Sandip Nirmel、Sebastian Oberhoff、Thomas Orton、Joshua Pan、Pablo Parrilo、Juan Perdomo、Banks Pickett、Aaron Sachs、Abdelrhman Saleh、Brian Sapozhnikov、Anthony Scemama、Peter Schäfer、Josh Seides、Alaisha Sharma、Nathan Sheely、Haneul Shin、Noah Singer、Matthew Smedberg、Miguel Solano、Hikari Sorensen、David Steurer、Alec Sun、Amol Surati、Everett Sussman、Marika Swanberg、Garrett Tanzer、Eric Thomas、Sarah Turnill、Salil Vadhan、Patrick Watts、Jonah Weissman、Ryan Williams、Licheng Xu、Richard Xu、Wanqian Yang、Elizabeth Yeoh-Wang、Josh Zelinsky、Fred Zhang、Grace Zhang、Alex Zhao 与 Jessica Zhu。 在本书的排版与制作过程中,我使用了许多开源软件包,对此我满怀感激。特别感谢 Donald Knuth 与 Leslie Lamport 创造了 LaTeX,以及 John MacFarlane 开发了 Pandoc。David Steurer 编写了最初用于生成此文本的脚本。当前版本使用了 Sergio Correia 的 panflute。LaTeX 与 HTML 模板源自 Tufte LaTeX、Gitbook 和 Bookdown。感谢 Amy Hendrickson 提供的 LaTeX 咨询。Juan Esteller 与 Gabe Montague 最初用 OCaml 与 JavaScript 实现了 NAND* 编程语言。我使用 Jupyter 项目编写了补充代码片段。
最后,我要感谢我的家人:我的妻子 Ravit,以及我的孩子 Alma 与 Goren。撰写本书(以及相应的课程)占用了我大量时间,以至于 Alma 在她的五年级作文中写道:“大学不应当逼迫教授过度工作。”遗憾的是,我所能展示的成果,似乎只是 600 页极度枯燥的数学文字。
❗页面施工中: 目前状态: 创建教程中.
要求:
- ✅将所有numthm环境用灰色admonish(quote)框起.
- ✅标点符号统一为英文.
- ✅使用添加对文内特定位置的超链接.
- ✅使用添加引用.
- ⬛️重要概念框.
格式统一教程: 标题
随机引的名人名言, 用quote括起 – 译者, 2025
学习目标
- 此处填写学习目标
- 一些目标
- 二些目标
- 三些目标
目录
以下是教程正文.
-
每一章以一些插图引入比较合适, 如下图, 然后再写正文前的引子.
-
使用
<span>即可添加能够超链接的ID (源码:[引用](#templateimage)), 点击即可跳转. -
原文中用斜体强调的词, 在译文中统一用加粗, 如:
You might think that the “best” algorithm for multiplying numbers will differ if you implement it in Python on a modern laptop than if you use pen and paper.
译作
例如, 你也许会认为, 在现代笔记本电脑上用 Python 实现的乘法算法, 与用纸笔进行乘法运算时的“最佳“算法会有所不同.
- 对某一章的引用可以直接引
.md: 例如本章 ([本章](chapter_x.md)), 对章节的引用则使用html id语法糖, 如下方x.1小节([x.1小节](#templatesection))所示.
x.1 小节: 右侧花括号添加 #id 即可用于引用
-
渲染时看不到上面说的花括号, 实际语句是:
## x.1 小节: 右侧花括号添加 #id 即可用于引用 { #templatesection } -
quote 可以带标题, 遵照原文即可. 当原文需要引用的时候, 就使用 quote.
举例来说: “一个平方加上它的十倍平方根等于三十九迪拉姆. “ 换句话说, 求这样一个平方数: 它加上它自身的十倍平方根, 结果是三十九.
解法如下:
(见Chapter 3)
因此, 这个平方根为三, 对应的平方为九.
- 代码块照常写即可.
# 使用 Python 的 sqrt 函数来计算平方根
def solve_eq(b, c):
# 根据 al-Khwarizmi 的方法求解 x^2 + b*x = c
blablabla()
# 测试: 求解 x^2 + 10*x = 39
print(solve_eq(10, 39))
-
出现在公式中的函数名全部应该用
\text框起, 如 ($\text{XOR}$). 如果发现某个名字经常出现, 应该将其添加进./makros.txt. 如与( 或( 非( ($\AND, \OR, \NOT$) -
example 环境的示例. 注意其中嵌套了代码, 所以使用了
~~~取代 ```. admonish的title中如果需要使用公式, 反斜杠需要重复三次. 例如下方的标题就出现了$\\\text{MAJ}$.
考虑函数 其定义如下:
(…)
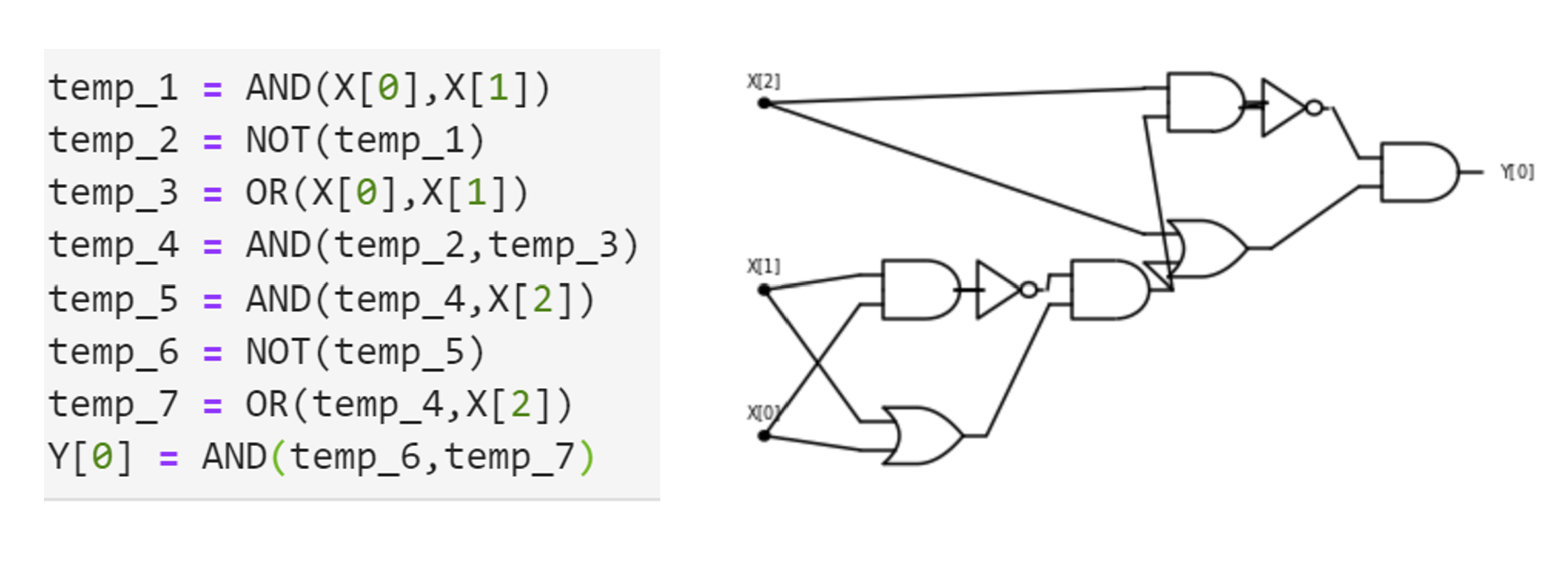
我们也可以将公式 (3.1) 以“编程语言“的形式表示: 将其表达为一组指令, 用于在给定基本操作 的情况下计算
def MAJ(X[0],X[1],X[2]):
firstpair = AND(X[0],X[1])
secondpair = AND(X[1],X[2])
thirdpair = AND(X[0],X[2])
temp = OR(secondpair,thirdpair)
return OR(firstpair,temp)
- 公式的引用: 在行间公式中添加
[{numeq}]{id}, 例如: 然后就可以直接引用: (1) ([{eqref: templatenumeq}])(为防止替换, 这里最外层的花括号替换成了方括号.)
x.1.1 依然是小节名示例. 小节名总是可以添加id.
- 所有 preprocessor
numthm引入的定理/例子/命题环境都需要套一个 admonish quote, 以和正文分隔开.book.toml中可以自定义这些环境. 已经定义了一些“常用缩写+c“为名的中文环境. 例如:
引理 1. 对于每个 在输入 时, 算法 3.1 输出
-
numthm的引用方式: 引理 1 ([{ref: templatelem}]) (为防止替换, 这里最外层的花括号替换成了方括号.) -
小练习对应的 admonish solution 以及证明对应的 admonish proof 应该是 collapsible 的. 如:
解答
解答
我们可以通过枚举 的所有 种可能取值来证明这一点, 但它也可以直接从标准的分配律推导出来.
假设我们将任意正整数视为“真“, 将零视为“假“. 那么对于每个数 为正当且仅当 为真, 而 为正当且仅当 为真.
这意味着对于每个 表达式 为真当且仅当 为正, 而表达式 为真当且仅当 为正.
根据标准的分配律 因此前者表达式为真当且仅当后者表达式为真.
对[{ref:id}]的证明
对[{ref:id}]的证明
对于任意 有 当且仅当 与 不同.
令 则在输入 时, 算法 3.1 输出
-
如果 则 因此输出为
-
如果 则 所以 输出为
-
如果 且 (或反之) , 则 且 此时算法输出
- 原文的 pause 也有对应的 admonish:
- 算法的写法, 以下是一个例子:
当然, 与图片一样, 也可以使用llm帮助转换.
依照示例, 将以下格式的算法转换为tex格式:
Input: $a,b \in \{0,1\}.$
Output: $XOR(a,b)$
$w1 \leftarrow AND(a,b)$
$w2 \leftarrow NOT(w1)$
$w3 \leftarrow OR(a,b)$
return $AND(w2,w3)$
转换为
$
\begin{array}{l}
\mathbf{Input:}\ a,b \in \{0,1\} \\
\mathbf{Output:}\ \XOR(a,b) \\
\hline
\mathbf{Step 1:}\ w_1 \leftarrow \AND(a,b) \\
\mathbf{Step 2:}\ w_2 \leftarrow \NOT(w_1) \\
\mathbf{Step 3:}\ w_3 \leftarrow\OR(a,b) \\
\mathbf{Step 4: return}\ \AND(w_2,w_3)
\end{array}
$
我将提供其它类似格式的算法输入.
-
脚注的例子 1 (
[{footnote: 这是一条脚注}]). 最外层的方括号替换为花括号, 文中出现脚注时需要使用. -
正文结束后, 用 admonish hint 写回顾
x.2 小节: 各类环境使用方式汇总
x.2.1 admonish
- 插入图片: 用pic环境框起, 再付一个numthm的pic编号环境. 源码:
```admonish pic id = '图片id'

<-- 这里的空行不能省
[{pic}] 图片描述 <-- 外层花括号改为方括号, 和描述之间的空格不能省
```
效果如下, 引用可直接使用pic id:
图 1. 这是图片描述.
插入图片的格式可以设计prompt交给llm处理. 下面给一个例子
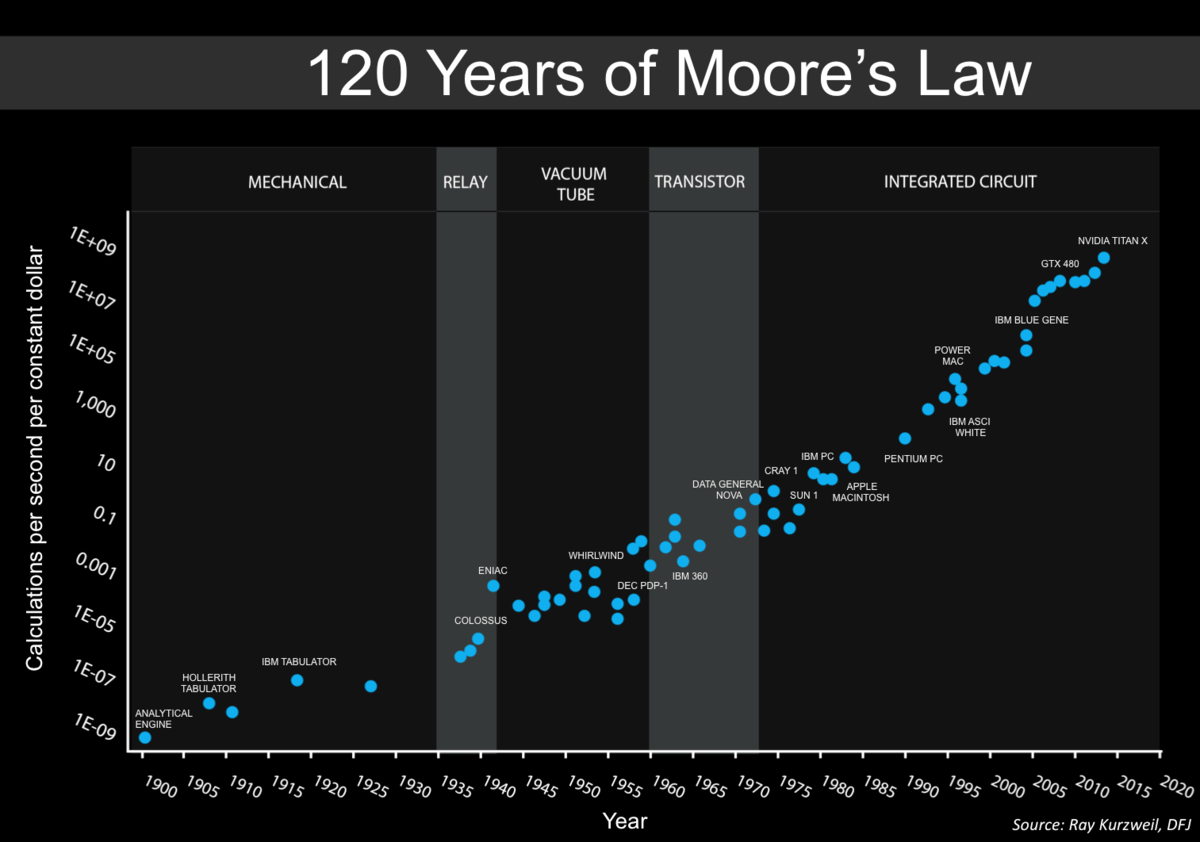
请根据以下例子转换插入图片的格式:
{#moorefig .margin}
转换为
```admonish pic id = "moorefig"

[{pic}] 1959 至 1965 年间集成电路中的晶体管数量,并预测指数级增长至少能持续十年。取自戈登·摩尔 1965 年的文章 *Cramming More Components onto Integrated Circuits*。
```
我将提供其它相同格式的代码, 输出请装在代码块内: 要再套一层代码块, 而不是使用已有的.
- 原文出现的 Big Idea(重要启示):
习题
- 习题的专有
numthm环境是proc. 例如:
- 依然可以先翻译习题(和标题), 再用llm调整格式, 以下是可用的prompt.
改变以下我输入的习题框的格式: 例如
::: {.exercise title="比较 $4$bit 数字" #comparenumbersex}
给出一个布尔电路(使用 $\AND/\OR/\NOT$ 门),该电路计算函数 $ \text{CMP}_8:\{0,1\}^8 \rightarrow \{0,1\}$,使得当且仅当由 $a_0a_1a_2a_3$ 表示的数大于由 $b_0b_1b_2b_3$ 表示的数时,$ \text{CMP}_8(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)=1$。
:::
改为
[{proc}]{comparenumbersex}[比较 $4$bit 数字]
给出一个布尔电路(使用 $\AND/\OR/\NOT$ 门),该电路计算函数 $ \text{CMP}_8:\{0,1\}^8 \rightarrow \{0,1\}$,使得当且仅当由 $a_0a_1a_2a_3$ 表示的数大于由 $b_0b_1b_2b_3$ 表示的数时,$ \text{CMP}_8(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)=1$。
接下来我将提供输入.
注意上面proc的方括号要改掉.
杂记
- 杂记需要修复对文献的引用. 使用
<a>编写引用.
未完成章节中的引用:
以下是未完成的章节中的引用
1: 这是一条脚注
引言
学习目标
- 介绍并激发对“计算“本身的研究兴趣, 而不局限于具体的实现方式.
- 了解算法(Algorithm)这一概念及其发展历程.
- 算法不只是一种工具, 更是一种思考和理解的方式.
- 领略大O分析法(Big- analysis)和高效算法设计中蕴含的惊人创造力.
“我的演讲主题或许可以通过提出两个简单的问题来最直接地揭示: 首先, 乘法是否比加法更难? 其次, 为什么? …….我(想)证明, 在计算上, 没有跟加法一样简单的乘法算法, 这证明了一些理论上的绊脚石的存在. “
—Alan Cobham, 1964年
位值数字系统(place-value number system)古巴比伦人最大的发明之一. 在位值数字系统中, 数字(number)被表示为一串数位(digit)序列, 其中每个数位的位置决定了其数值.
这与类似罗马数字的系统刚好相反, 在罗马数字中, 每个数位无论其在数字中的位置如何, 均有一个不变的值. 举个例子, 地球到月球的平均距离大概是259956罗马英里. 在标准罗马数字中, 这个数字的表示为:
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
MMMMMMMMMMMMMMMMMMMDCCCCLVI
使用罗马数字表示地球到太阳的距离需要大概100000个符号, 而我们需要一本50页的书来书写这一个数字!
对于那些习惯于像罗马数字那样以加法系统来思考数字的人来说, 诸如地球到月球距离的这种数字不仅仅是大—它们无法形容: 这些数字不能被有效地表达甚至是理解. 这也难怪第一个计算地球直径的埃拉托色尼(计算误差约为10%), 和第一个计算地球与月球之间距离的喜帕恰斯使用了古巴比伦的六十进制位值数字系统, 而不是使用罗马数字系统.
0.1 整数的乘法: 一个算法示例
在计算机科学的语言中, 这种用于表示数字的位值系统是一种数据结构(data structure), 数据结构是一组用于将对象表示为符号的指令或“配方“. 而算法(algorithm)则是在此类表示形式上执行操作的一组指令或“配方“. 数据结构与算法不仅催生了改变人类社会的惊人应用, 其重要性更远超实用价值. 比特(bit)、字符串(string)、图(graph), 乃至程序本身等计算机科学体系中的数据结构, 以及普适性、复制等概念, 不仅被广泛应用于实践领域, 更催生了一种全新的语言和审视世界的方式.
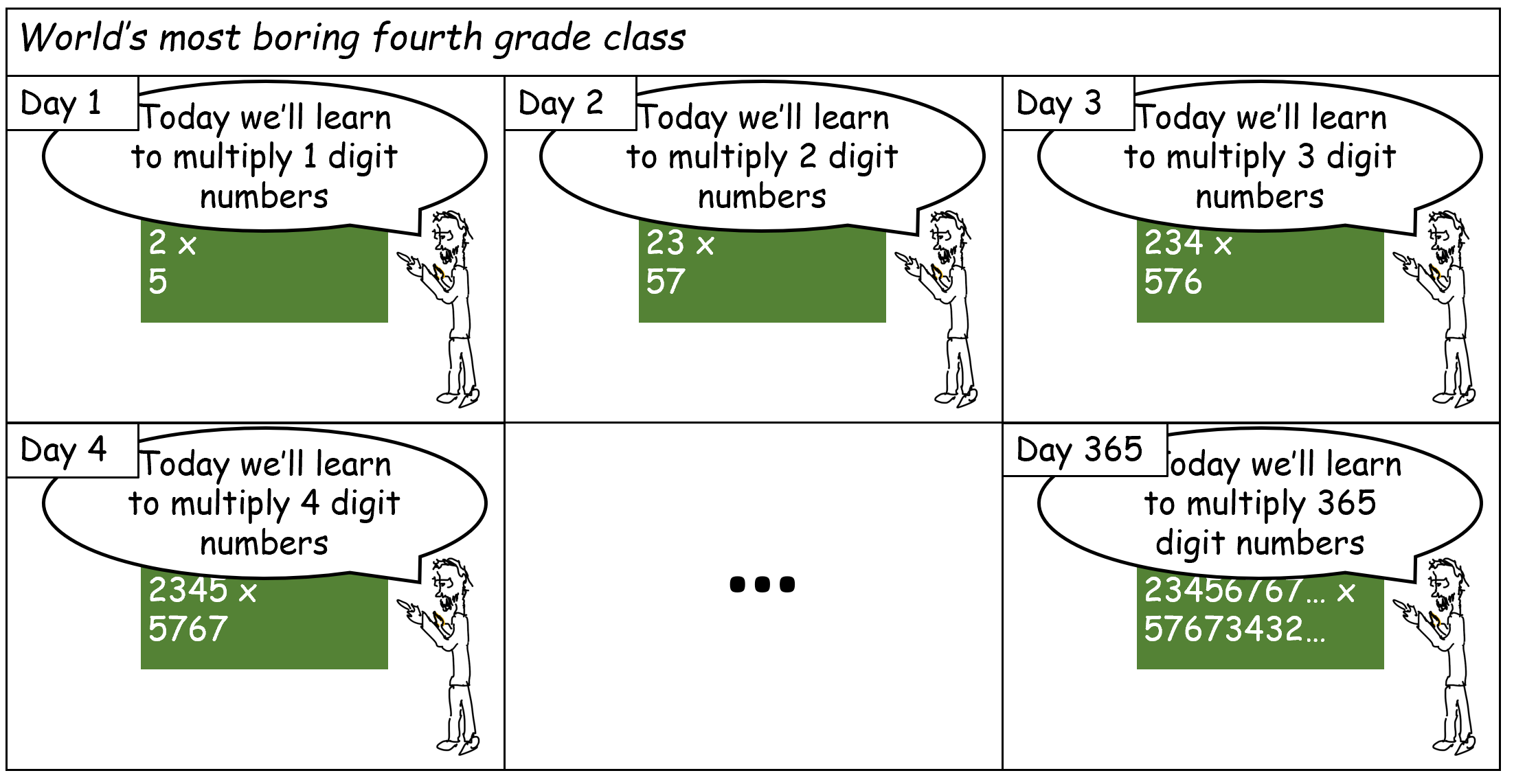
除了位值数字系统, 古巴比伦人还发明了我们在小学中都学过的加法和乘法的“标准算法“. 这些算法在漫长的历史中始终至关重要, 无论是使用算盘、莎草纸还是纸笔计算的人们均受惠于此, 但在计算机的时代, 除了折磨小学三年级学生之外, 这些算法是否还有存在的价值? 为了说明这些算法为何至今仍具有重要意义, 让我们将古巴比伦人的逐位相乘算法(即“小学乘法“)与通过重复相加实现的朴素乘法算法进行对比. 我们首先正式描述这两种算法, 详见算法 1和算法 2:
算法 6.1和算法 2均假定我们已经掌握了数字相加的方法, 而算法 2还假定我们能够将数字与10的幂相乘(毕竟这只相当于一次简单的移位). 假设和是两个位的十进制整数(这大致相当于64位二进制数, 也是许多编程语言中常见的类型). 使用算法 6.1计算需要将自身相加次. 由于有20位, 这意味着我们需要至少进行次加法运算. 相比之下, 算法 2仅需次移位和单位数字的乘法运算, 因此最多仅需次单位数字的操作. 为了理解这种差异, 假设一个小学生完成单位数字的操作需要2秒, 那么使用算法 2计算需要约1600秒(约半小时). 反之, 即使现代计算机的运算速度比人类快十亿倍以上, 若采用算法 6.1进行计算, 则需要秒(超过3000年! )才能得到相同的结果.
计算机从未使算法过时. 恰恰相反, 随着人类测量、存储和传输数据的能力的大幅提升, 我们比以往更需要开发精密而高效的算法, 从而基于数据洪流做出更明智的决策. 我们也不难发现: 算法的概念在很大程度上独立于实际执行计算操作的设备. 无论是硅基芯片还是借助纸笔计算的小学三年级学生, 逐位相乘的算法都远胜于重复累加法.
理论计算机科学专注于研究算法和计算的内在属性—即那些独立于现有技术而存在的本质特征. 我们既探讨古巴比伦人早已思索过的问题(比如“什么是两数相乘的最优方法“), 也研究依赖前沿科技的课题(例如“能否利用量子纠缠效应实现更快速的因数分解“).
备注 1 (算法的规范, 实现和分析). 一个算法的完整描述包括三个部分:
- 规范(specification): 算法完成了什么任务, 即做了什么(例如, 算法 6.1和算法 2进行的乘法).
- 实现(implementation): 如何完成算法的任务, 即如何做. 即使算法 6.1与算法 2完成的是同样的两数相乘的乘法, 它们的实现方式并不相同(即两个算法具有不同的实现).
- 分析(analysis): 为什么组成算法的这一系列指令能够完成它的任务. 一个对于算法 6.1和算法 2的完整描述包含一个证明, 证明这两个算法在接受到输入的时候的确会输出两数的乘积
一般来说, 算法的分析不仅会包含对算法的正确性分析, 还会包含对算法高效性的分析. 也就是说, 我们不仅想证明算法完成了预计的任务, 而且会在规定的次数内完成. 比如说, 算法 2使用了次操作完成了对位数字的乘法, 而算法 3(在下一节中介绍)使用了次操作完成了同样的操作(我们会在[第1.4.8节]{chapter_1.md#secbigohnotation}中定义大表示法)
0.2 扩展示例: 一种更快的乘法方法(可选)
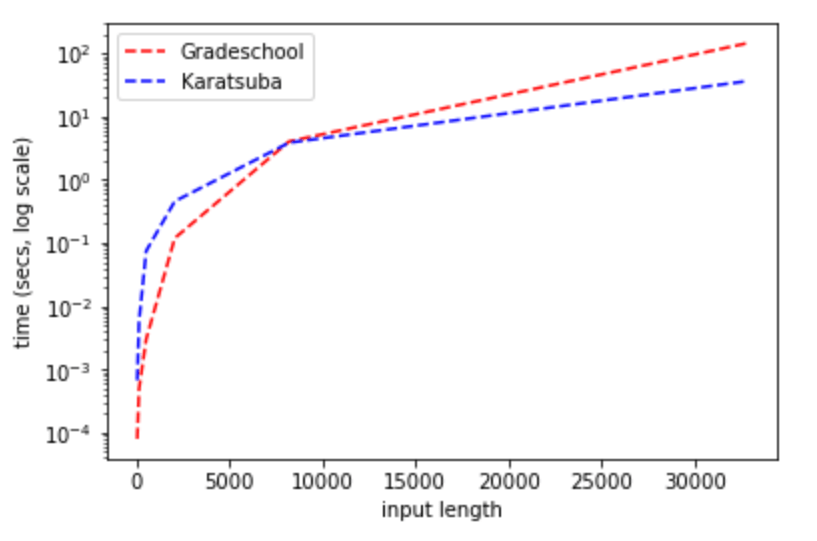
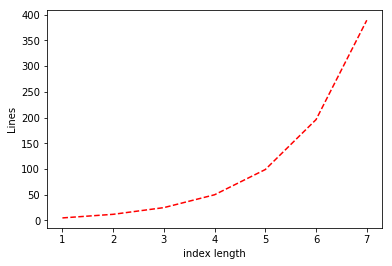
一旦你想到标准的逐位相乘乘法, 它似乎是“显然最优“的数字相乘方式. 1960年, 著名数学家安德雷·柯尔莫哥洛夫(Andrey Kolmogorov)在莫斯科国立大学组织了一场研讨会, 他在会上提出猜想: 任何两个位数相乘的算法都需要执行与成正比的基本操作次数(用第一章定义的大符号表示为次操作). 换言之, 柯尔莫哥洛夫认为在任何乘法算法中, 相乘的数字位数翻倍会导致所需基本操作次数变为四倍. 当时听众中有一位名叫阿纳托利·卡拉楚巴(Anatoly Karatsuba), 他在一周内就推翻了柯尔莫哥洛夫的猜想—他发现了一种仅需次操作(为常数)的算法. 随着增大, 这个数字会远小于 因此对于大数而言, 卡拉楚巴算法优于小学算法. (例如Python在处理1000比特及以上的数字时, 会从小学算法切换至卡拉楚巴算法. )虽然与算法之间的差异有时在实践中至关重要(参见下文的0.3节), 但本书将基本忽略这类区别. 不过我们仍会在下文介绍卡拉楚巴算法, 因为它完美展现了算法往往出人意料的特性, 同时也体现了算法分析的重要性—这正是本书乃至整个理论计算机科学的核心所在.
卡拉楚巴算法基于一种两位数字之间的更快的相乘算法. 假设是一对两位数字. 我们使用表示的十位上数字, 表示个位上的数字, 所以可以表示为 亦可写成 这里 图 1展示了两位数字的小学乘法.
小学乘法的算法可以看作一个将两位数字相乘的任务转化为四个单位数字相乘的过程:
通常, 在小学算法中, 输入数字位数翻倍会导致操作次数变为原来的四倍, 从而形成时间复杂度的算法. 相比之下, 卡拉楚巴算法基于这样一个观察: 我们同样可以将(1)表示为:
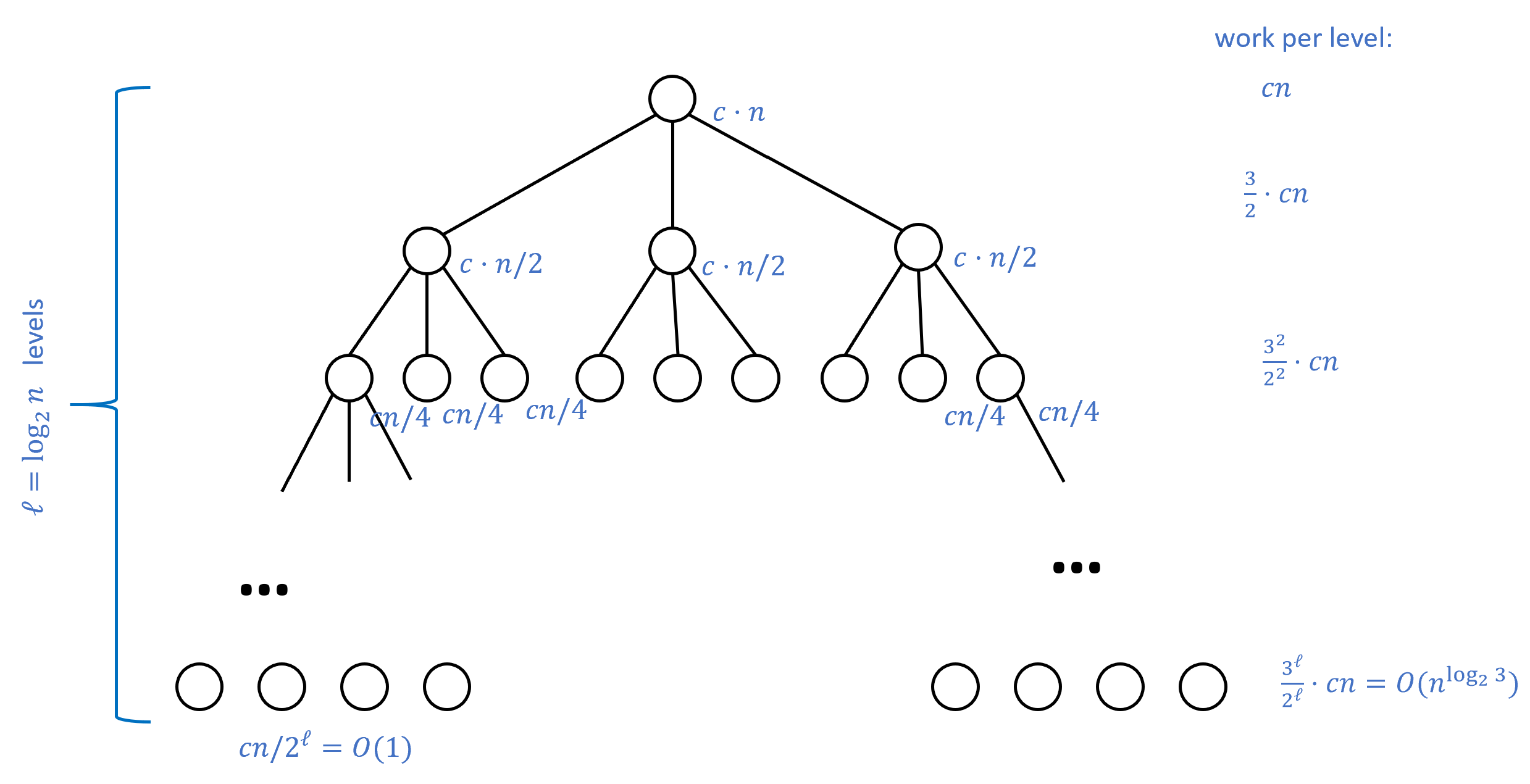
这将两位数字的乘法简化为了以下三个更简单的乘积计算: 、以及 通过递归地重复相同策略, 我们可以将两个位数相乘的任务简化为三对位数相乘的任务. 由于每当数字位数翻倍时, 操作次数会变为三倍, 因此当时, 我们可以使用约次操作完成乘法运算.
上述内容是卡拉楚巴算法背后的直观思想, 但尚不足以完整描述该算法. 一个算法的完整描述需要包含其操作步骤的精确说明以及算法分析: 即证明该算法确实能实现预设任务. 卡拉楚巴算法的具体操作步骤见算法 3, 其数学分析则包含在引理 1和引理 2中.
算法 3只是卡拉楚巴算法完整描述的一半, 另一半是算法的分析, 即证明(1)算法 3确实完成了乘法的计算以及(2)它确实使用了步操作来完成计算. 我们首先从证明(1)开始:
对于任意的两个非负整数 当输入时, 算法 3的输出为
对引理 1的证明
对引理 1的证明
假设输入为最多有位的整数, 算法 3将会用次操作来进行计算.
对引理 2的证明
对引理 2的证明
卡拉楚巴算法远非乘法算法的终点. 20世纪60年代, 图姆(Toom)和库克(Cook)扩展了卡拉楚巴的思想, 提出了时间复杂度为(为常数)的乘法算法. 1971年, 舍恩哈格(Schönhage)和施特拉森(Strassen)利用快速傅里叶变换实现了更优的算法——其核心思想是将整数视为“信号“, 通过转换到傅里叶域来更高效地完成乘法运算(傅里叶变换是数学和工程学的核心工具, 应用极其广泛; 若您尚未接触过, 很可能在后续学习中会遇到). 此后多年间, 研究者们不断改进算法, 直到最近哈维(Harvery)和范德霍芬(Van Der Hoeven)才成功实现了时间复杂度为的乘法算法(不过该算法仅在处理真正天文级别的数字时才开始超越舍恩哈格-施特拉森算法). 然而, 尽管取得了这些进展, 我们至今仍未知晓是否存在能在时间内完成两个位数乘法的算法!
本书包含许多“进阶“或“选读“的注释与章节. 这些内容可能需要学生具备特定基础知识方可理解, 但均可放心跳过, 因为后续章节均不依赖这些内容. )
与卡拉楚巴算法相似的思路也可用于加速矩阵乘法运算. 矩阵是表示线性方程与线性运算的强大工具, 被广泛应用于科学计算、图形学、机器学习等众多领域.
矩阵的基本运算之一便是矩阵乘法. 例如若有矩阵和 则其乘积为 可见该乘积可以通过8次数值乘法来计算.
现假设为偶数, 和为一对的矩阵, 与均可被划分为四个的块: 和 此时的矩阵乘积的表示与上述公式完全一致, 只需将数值的乘积替换为对应的矩阵乘积, 数值加法替换为对应的矩阵加法即可. 这意味着我们可以通过使用上述公式来给出一个算法, 该算法在输入矩阵维度倍增的同时, 所需的操作数量提升为原来的8倍—即当时, 总操作量将达到次.
1969年, 福尔克·施特拉森(Volker Strassen)提出通过对以下七项进行加减运算, 即可仅用7次数值乘法完成二维矩阵求积: 可验证其满足:
基于这一发现, 我们可以获得一个算法, 使得矩阵维度倍增时运输量仅增加至7倍. 这意味着当时, 总计算成本为 经过一系列后续研究改进, 当前最优算法的时间复杂度已达约 然而与整数乘法不同的是, 目前我们尚未发现能在线性或近似线性时间内(例如完成矩阵乘法的算法. 尽管研究者们尝试运用群表示理论(可视为傅里叶变换的推广)来寻求更快的算法, 但至今为止此项努力尚未取得成功.
0.3 超越算术的算法
对更优算法的探索绝非仅限于加法、乘法或解方程等算术任务. 在过去的数十年间, 图论算法领域涌现出大量突破性成果—包括路径搜索、匹配、生成树、割集和流算法在内的多项发现, 这一领域至今仍是密集研究的重点领域(例如近年来基于电路理论与线性方程求解器之间的意外关联产生了诸多最大流问题上的进展. )这些算法不止被应用于网络流量路由、GPS导航等“天然“应用场景, 更广泛渗透于基因交互图谱结构促进新药研发、投资关联风险计算等多元化领域.
谷歌公司的成立基石是PageRank算法—该算法能够高效地近似计算网络图邻接矩阵(经阻尼处理过后的)的“主特征向量(principle eigenvector)“. Akamai公司的诞生则依托于创新数据结构“一致性哈希”, 该数据结构能够实现哈希桶在多服务器之间的分布式存储. 反向传播算法(backpropagation algorithm)通过将神经网络偏导数计算复杂度从降至 成为深度神经网络近年取得惊人成就的核心支柱. 而基于稀疏约束线性方程求解的压缩感知(compressed sensing)算法, 显著降低了MRI图像分析对数据量和质量的要求, 这一突破对于儿童肿瘤MRI检测具有革命性意义—此前医生需实施麻醉暂停患儿呼吸进行扫描, 此过程常常伴随致命风险.
即便对于毕达哥拉斯时代就开始研究的素数判定这类经典问题, 仍有不断的新发现涌现: 高效的概率算法于1970年代问世, 首个确定性多项式时间算法直至2002年才被发现. 在合数分解这个领域, 1980年代诞生了新算法, 而1990年代的研究成果(本课程后续将继续探讨)更揭示了利用量子力学实现加速算法的诱人前景.
尽管取得诸多进展, 算法领域仍存在悬而未解之谜. 对于大多数自然问题, 我们既无法断定现有算法是否已达到最优, 亦不能确定是否存在更高效的待发现算法. 正如本章开篇引用的Cobham论断所示——即便是数字乘法这个基础问题, 我们至今仍未证明是否存在与加法算法同等高效的乘法算法. 但至少, 我们已掌握了正确的追问方式.
0.4 论负面结果的重要性
寻找更好的算法来解决诸如乘法、解方程、图论问题或将神经网络拟合数据等问题, 无疑是值得付出努力的. 但为何证明这类算法不存在也同样重要? 其中一个动机源于纯粹的好奇心. 研究不可行性结果的另一个原因在于, 它们对应着我们世界的根本限制. 换而言之, 不可行性结果即是自然法则.
以下是一些计算机科学领域之外的不可行性案例(更多案例参见0.7节). 物理学中, 制造永动机的不可能性对应着能量守恒定律; 热机无法突破卡诺定律的限制对应着热力学第二定律; 而超光速信息传输的不可能性则是狭义相对论的基石. 数学领域中, 虽然我们在高中都学过解二次方程的公式, 但将这种公式推广到五次及以上方程的不可能性催生了群论; 无法从前四个公设证明欧几里得第五公设则导致了非欧几何的诞生——这种几何体系最终成为广义相对论的关键基础.
类似地, 计算领域的不可行性结果对应着“计算法则“, 这些法则揭示了任何信息处理装置(无论是基于硅基芯片、神经元还是量子粒子)的根本限制. 更重要的是, 计算机科学家创造了巧妙的方法来利用计算局限性完成特定任务. 例如现代互联网通信大多采用RSA加密方案, 其安全性正是基于(推测性的)大整数高效分解的不可能性; 近年来比特币系统采用“数字金本位“模式——通过“挖矿“解决计算难题来获取新型货币, 而非依赖贵金属支撑.
- 算法的历史可追溯至数千年前, 它们不仅是人类进步的重要推动力, 如今更构成了价值数十亿美元的产业基础与拯救生命的技术核心.
- 实现同一计算任务往往存在多种算法, 找到更高效的算法通常比改进计算硬件能带来更显著的提升.
- 优秀的算法和数据结构不仅能加速计算, 更能带来认知上的飞跃.
- 我们将探讨的核心问题是如何为给定问题寻找最优算法.
- 要证明某个算法是解决特定问题的最优方案, 就必须证明不可能以更少的计算资源解决该问题.
0.5 本书其余部分的路线图
通常, 当我们试图解决计算问题时—无论是求解线性方程组、寻找矩阵的主特征向量, 还是对网络搜索结果进行排序—采用“一目了然“的标准来描述算法通常已经完全足够. 只要我们找到了解决问题的某种方法, 便会感到满意, 可能并不关心这些解决方法中算法的精确数学模型. 但当我们需要回答诸如“是否存在解决问题的算法? “这类问题时, 就必须在数学上进行更精确的界定.
具体而言, 我们需要: (1)明确定义“解决“的含义, (2)精确定义什么是算法. 有时即使是解决(1)也并非易事, 而(2)则尤其具有挑战性—我们如何(甚至能否)囊括所有潜在的算法设计方法尚未明确. 我们将考察几种简化的计算模型, 并论证尽管这些模型形式简洁, 却足以涵盖所有“合理“的计算实现方式, 包括现代计算设备中采用的所有方法.
一旦我们拥有了这些描述计算的形式化的模型, 我们就能尝试论证计算任务的不可能性, 证明某些问题无法被解决(或者可能无法在我们宇宙的资源限制内解决). 阿基米德有言: 只要给他一个支点和足够长的杠杆, 他就能撬动地球. 我们将看到归约方法如何将一项计算困难度结论转换为众多问题的解决方案, 从而清晰界定可计算和不可计算(或易处理与难处理)问题之间的边界.
在后续章节中, 我们将重新审视计算模型, 探讨随机性或量子纠缠等资源具有的改变这些模型的潜力. 在涉及概率算法的内容中, 我们将窥见随机性如何成为理解计算、信息与通信不可或缺的工具. 同时我们也将认识到, 计算难度可以转化为优势而非障碍, 并且可以用于实现概率算法的“去随机化“. 这些思想同样体现在密码学中—该领域在过去几十年不仅经历的技术革命, 更完成了智力层面的革新, 其诸多成就都构建于本课程探讨的基础之上.
理论计算机科学是一个博大精深的领域, 其分支触及众多科学与工程学科. 本书仅呈现了这个领域非常局部(且带有主观倾向)的样本. 最重要的是, 我希望能将本人对这个领域的热爱至少部分地“传染“给读者——这个深受实践联系启发与丰富的学科, 即便不考虑其应用价值, 其本身也蕴含着深邃而璀璨的美感.
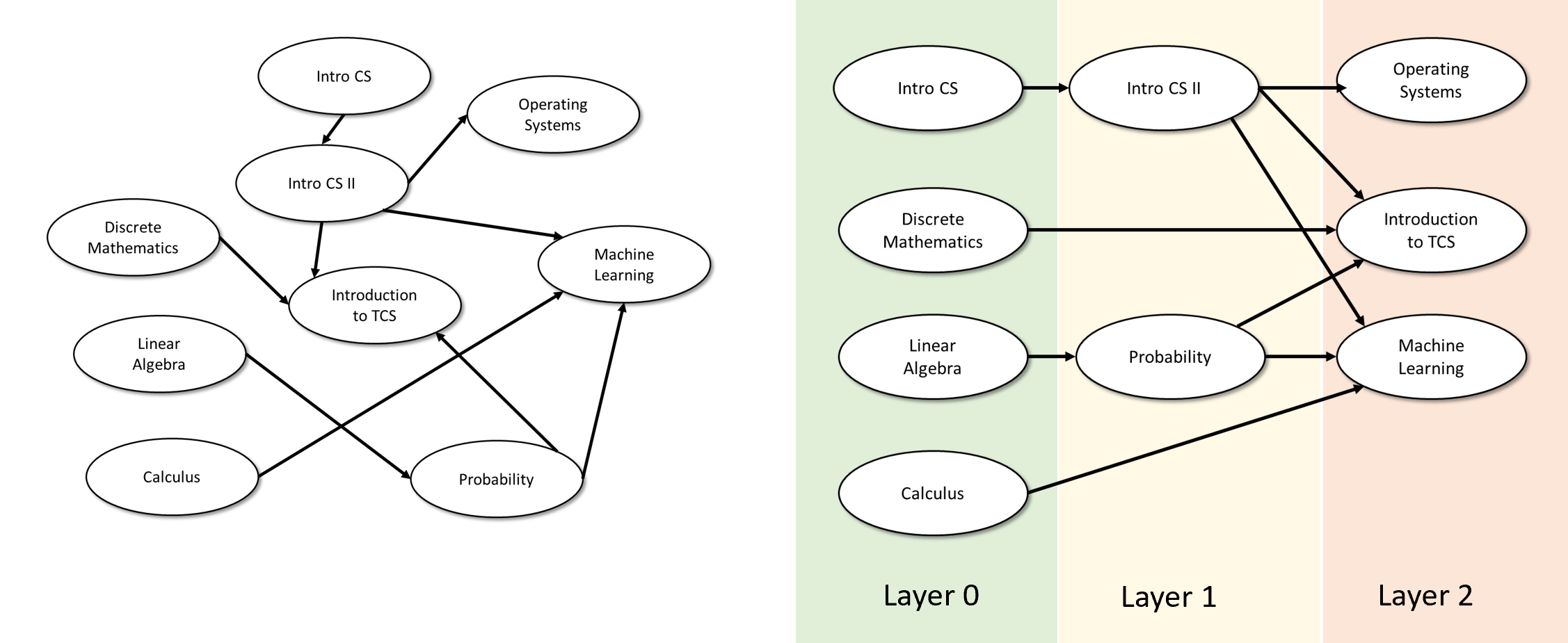
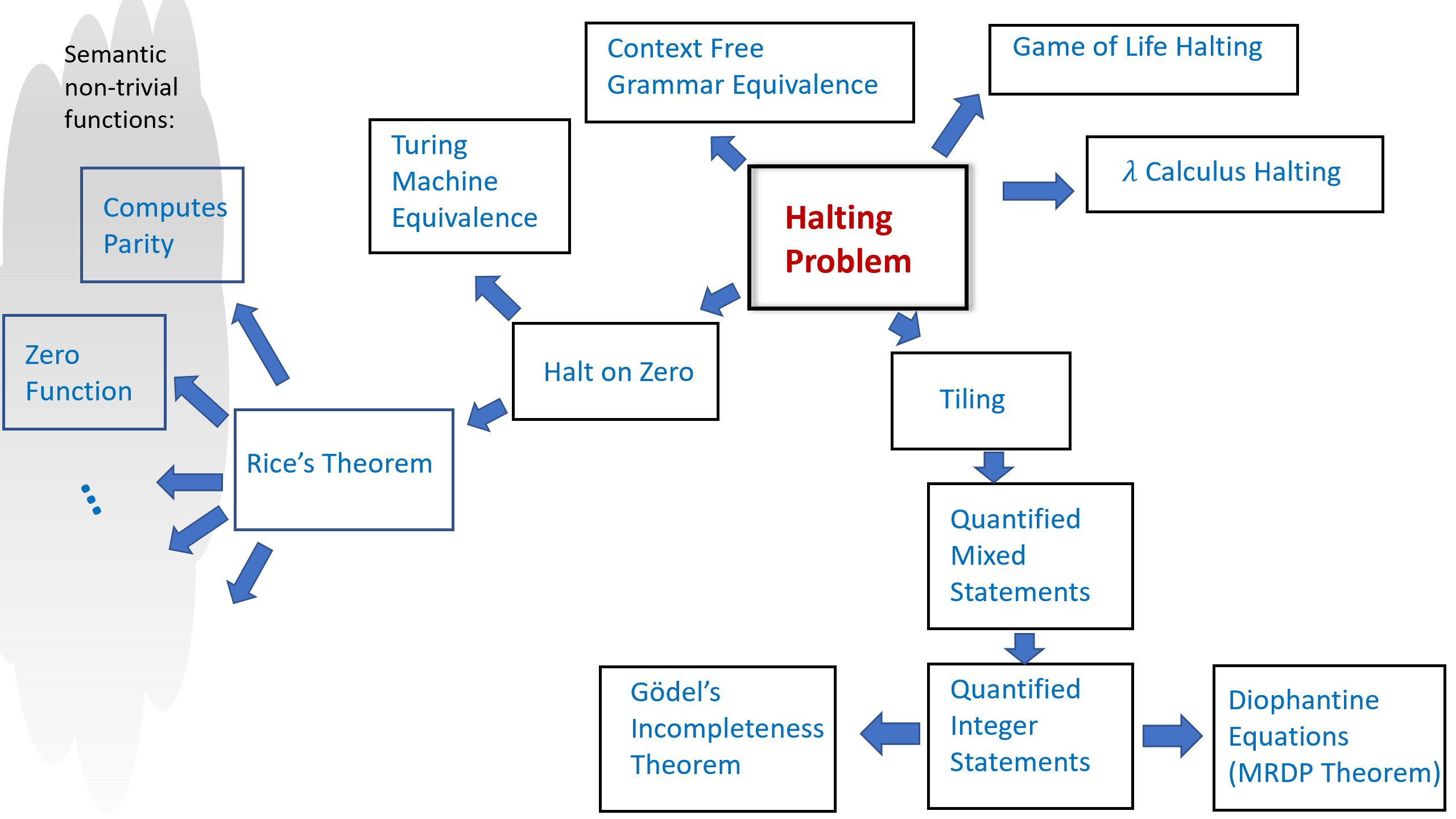
0.5.1 章节之间的依赖关系
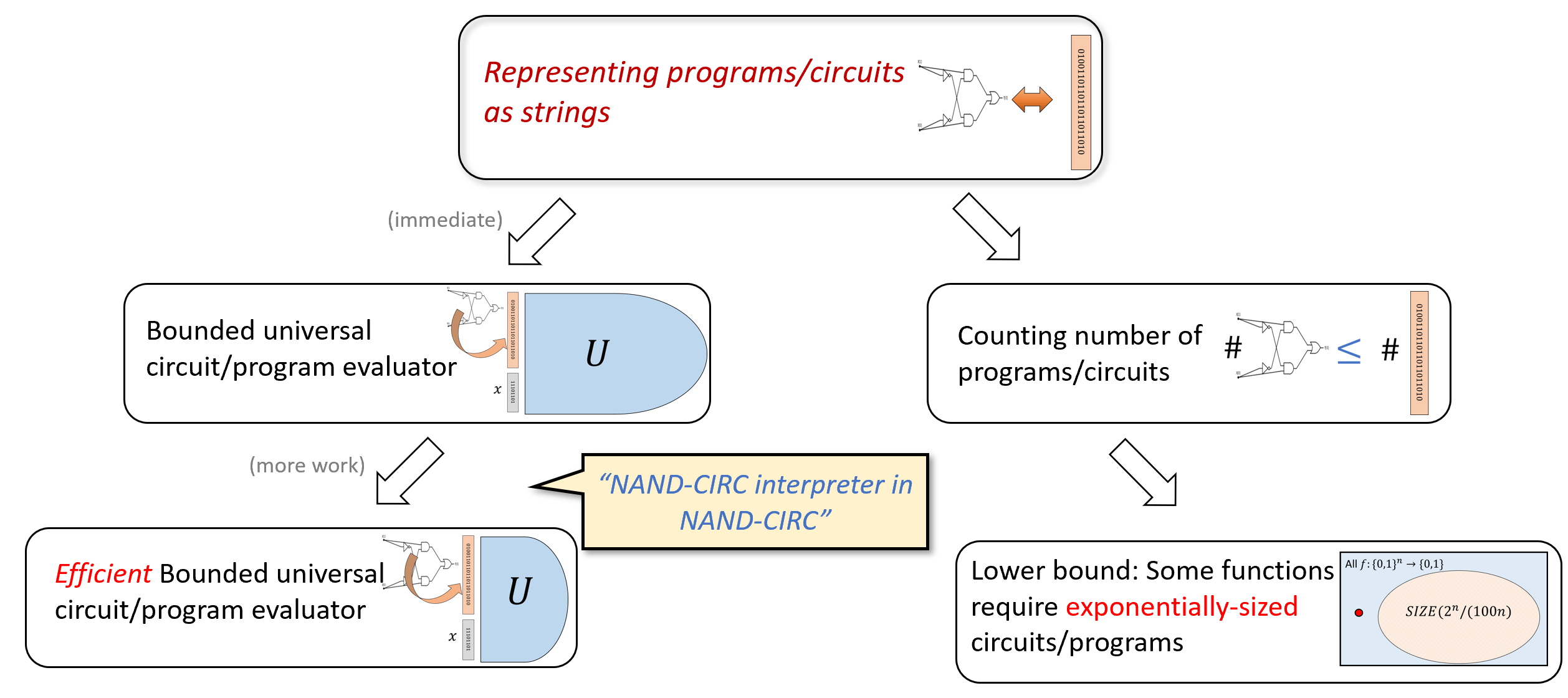
本书由以下数个部分组成, 见图0.5.
- 基础知识: 引言、数学背景、和将对象表示为字符串的方法.
- 第一部分: 有限计算(布尔电路) 电路与直线程序的等价性、通用门集合、任意函数的电路实现、电路的字符串表示、通用电路、计数论证法下的电路规模下界
- 第二部分: 均匀计算(图灵机) 图灵机与循环程序的等价性、计算模型等价性(包括RAM机器、演算与元胞自动机)、图灵机构型、通用图灵机存在性、不可计算函数(包括停机问题与Rice定理)、Gödel不完备定理、受限计算模型(正则语言与上下文无关语言)
- 第三部分: 高效计算 时间复杂度定义、时间分层定理、与复杂度类、复杂度类、完全性与Cook-Levin定理、空间受限计算
- 第四部分: 随机计算 概率基础、随机算法、复杂度类、错误率放大技术、定理、伪随机生成器与去随机化
- 第五部分: 高级专题 密码学、证明与算法(交互式证明与零知识证明、Curry-Howard对应关系)、量子计算
%%{init: {'theme':'dark'}}%%
graph TD;
p1[**第一部分:有限计算(布尔电路)**
**有限**输入上的函数
**定量**研究];
p2[**第二部分:均匀计算(图灵机)**
**无限**输入上的函数
**定性**研究];
p3[**第三部分:高效计算**
**任意长度**输入上的函数
**定量**研究];
p4[**第四部分随机计算**
均匀类和非均匀类的关系。将计算难度视为一种资源。];
p5[**第五部分:高级专题**];
p1==>p3;
p1-.->p2;
p2==>p3;
p3==>p4;
p4==>p5;
图 5. 不同部分之间的依赖结构. 第一部分介绍布尔电路模型, 用以研究有限函数, 重点讨论定量问题(计算一个函数需要多少个逻辑门). 第二部分介绍图灵机模型, 用以研究输入长度无界的函数, 重点讨论定性问题(函数是否可计算). 第二部分多数内容不依赖于第一部分, 因为图灵机可作为首个计算模型引入. 第三部分同时依赖于前两部分, 因其对输入长度无界的函数展开定量研究. 更进阶的第四部分(随机计算)和第五部分(高级专题)则依赖于前三部分的内容体系
本书主要采用线性叙事结构, 各章节内容环环相扣, 但以下例外情况请注意: 演算(第8.5节)、Gödel不完备定理(第11章)、自动机/正则表达式与上下文无关文法(第10章)以及空间受限计算(第17章)的内容在后续章节中不再使用, 教师可自主选择是否讲授这些章节.
第二部分(均匀计算/图灵机)不强烈依赖第一部分(有限计算/布尔电路)的内容, 稍作调整后可互换教学顺序. 布尔电路在第三部分(高效计算)用于证明和Cook-Levin定理, 在第四部分(用于证明和去随机化)以及第五部分(密码学和量子计算专题)中均有应用.
第五部分(高级专题)各章节内容相互独立, 可按任意顺序讲授.
基于本教材的课程建议完整覆盖第一、二、三部分(可选择跳过演算、第11章、第10章或第17章), 随后完整或部分讲授第四部分(随机计算), 最后根据师生兴趣精选第五部分的高级专题进行补充教学.
0.6 习题
习题 1.
评估下列发明在加速大数字(即100位或以上)乘法运算中的重要性. 通过粗略估算, 按它们相对于前一种情况所提供的加速倍率进行排序.
- 发现逐位相乘的小学算法(对重复加法进行改进).
- 发现卡拉楚巴算法(对逐位相乘算法进行改进).
- 现代电子计算机的发明(对纸笔计算进行改进).
习题 2.
1977年的苹果二代个人电脑(Apple II)处理器主频为1.023兆赫, 约每秒执行次操作. 在本文撰写时, 全球最快的超级计算机性能为93“帕秒浮点运算“(次浮点运算/秒), 约合每秒次基本操作. 针对以下每种时间复杂度(作为输入长度的函数), 分别计算这两类计算机在持续运行一周的情况下, 能处理多大规模的输入:
- 次操作
- 次操作
- 次操作
- 次操作
- 次操作
习题 3 (算法不存在性的实用价值).
本章提及了若干基于新算法发现而创立的企业. 能否举例说明基于算法不存在性而创立的企业? 提示见脚注2.
习题 5.
使用自选编程语言实现函数gradeschool_multiply(x,y)和karatsuba_multiply(x,y): 输入两个数字数组x和y(其中x对应数字x[0]+10*x[1]+100*x[2]+...), 分别采用小学算法和卡拉楚巴算法返回表示乘积的数组. 卡拉楚巴算法在多少位数时超越小学算法的性能?
本习题将证明: 若对某个 能用最多次乘法运算完成两个实值矩阵的乘积计算, 则对任意足够大的 我们能在约时间内完成两个矩阵的乘法.
为了使证明严谨, 我们需要引入一些略显繁琐的记号. 假设存在和 使得对任意满足的矩阵 都能对任意表示为:
其中为线性函数, 为系数集合. 证明在此假设下, 对任意 当足够大时, 存在最多使用次算术运算即可完成两个矩阵乘积计算的算法. 提示见脚注4.
0.7 参考书目
若要简要了解本书的主要内容, 伯纳德·查泽(Bernard Chazelle)论述《算法作为现代科学范式》的精彩文章是不可多得的优质资料. 摩尔与默滕斯的著作(Moore, Mertens, 2011)对计算理论进行了卓越而全面的概述, 涵盖本章及本书后续讨论的诸多内容. 阿伦森的专著(Aaronson, 2013)同样值得推荐, 其中探讨了许多相关主题.
关于巴比伦人使用的算法, 可参阅高德纳的论文和诺伊格鲍尔的经典著作. 本章提及的多数算法可见于以下教材: 科曼、莱瑟森、里维斯特和斯坦(Cormen, Leiserson, Rivest, Stein, 2009), 克莱伯格与塔多斯(Kleinberg, Tardos, 2006), 达斯古普塔、帕帕季米特里乌和瓦齐拉尼(Dasgupta, Papadimitriou, Vazirani, 2008), 以及杰夫·埃里克森的教材. 埃里克森的著作可免费在线获取, 其中对递归算法(特别是卡拉楚巴算法)进行了精彩论述.
卡拉楚巴在本人著作(Karatsuba, 1995)中讲述了发现乘法算法的经过. 如前所述, 图姆和库克(Toom, 1963)(Cook, 1966)、舍恩哈格与施特拉森(Schönhage, Strassen, 1971)、富雷尔(Fürer, 2007)以及近期的哈维与范德霍芬(Harvey, Van Der Hoeven, 2019)相继做出了改进, 相关综述可参阅这篇文章. 后两篇论文的关键基础是快速傅里叶变换算法. 约翰·图基在冷战背景下(重新)发现该算法的精彩故事记载于(Cooley, 1987)(之所以称为“重新发现“, 是因为后世研究表明该算法可追溯至高斯时代(Heideman, Johnson, Burrus, 1985)). 快速傅里叶变换在下文提及的部分著作及杰夫·埃里克森的在线课程中均有涉及, 另可参考大卫·奥斯汀的科普文章. 快速矩阵乘法由施特拉森(Strassen, 1969)首创, 此后该领域持续涌现研究成果, 推荐阅读布拉泽的自含式综述(Bläser, 2013).
神经网络快速求导的反向传播算法由韦伯斯发明(Werbos, 1974). 网页排名算法由拉里·佩奇和谢尔盖·布林提出(Page, Brin, Motwani, Winograd, 1999), 与克莱伯格的HITS算法(Kleinberg, 1999)密切相关. 阿卡迈公司的创立基于一致性哈希数据结构(Karger, Lehman, Leighton, Panigrahy, Levine, Lewin, 1997). 压缩感知技术历史悠久, 其中两篇奠基性论文为(Candes, Romberg, Tao, 2006)和(Donoho, 2006). (Lustig, Donoho, Santos, Pauly, 2008)综述了压缩感知在MRI中的应用, 另可参阅埃伦伯格的科普文章(Ellenberg, 2010). 确定性多项式时间素性检测算法由阿格拉瓦尔、卡亚尔和萨克斯纳给出(Agrawal, Kayal, Saxena, 2004).
我们简要提及了数学中的经典不可行性结果, 包括欧几里得第五公设的不可证明性、尺规作图三等分角的不可能性, 以及五次方程无法通过根式求解的特性. 陶哲轩的博客文章给出了角三等分不可能性的几何证明(这是古希腊时期留下的三大几何难题之一). 马里奥·利维奥的著作(Livio, 2005)阐述了这些不可行性结论背后的背景与思想. 当前前沿研究正尝试运用计算复杂性解释物理学基本问题, 例如理解黑洞特性以及调和广义相对论与量子力学的矛盾.
1: 原文此处的内容为“Exercise 0.4“, 疑为作者笔误
2: 正如我们将在第21章(Chapter 21)中看到的, 几乎所有依赖密码学的企业都需要以某些算法的不存在性为前提. 特别地, RSA安全公司(RSA Security)的成立正是基于RSA加密系统的安全性, 该系统的前提正是假定不存在能高效计算大整数质因数分解的算法.
3: 提示: 使用归纳法进行证明——假设该结论对所有从到的值成立, 并证明其对同样成立.
4: 首先证明当(其中为自然数)时的特殊情况, 此时可通过将矩阵分割成块的方式进行递归处理.
- 数学背景
数学背景
学习目标
- 学习基本的数学概念, 如几何、函数、数字、逻辑运算符及量词、字符串和图.
- 严格地定义大表示法.
- 归纳证明法.
- 练习如何阅读数学 定义、陈述与证明.
- 将直观的论证转化为严谨的证明.
“我发现, 从一到十表达的每个数字, 都比前一个数字多一个单位: 之后, 十的倍数会翻倍或增至三倍……直至一百; 然后, 一百的倍数会以与个位和十位相同的方式翻倍和增至三倍……以此类推, 直至计数的最大极限. “,
—穆罕默德·伊本·穆萨·花拉子米(Muhammad ibn Mūsā al-Khwārizmī), 820年, 弗雷德里克·罗森(Fredric Rosen)译, 1831年
在本章中, 我们将会介绍一些将在本书中用到的数学概念. 这些概念一般会在“计算机科学中的数学“或“离散数学“等课程或课本中讲解. 有关这些主题的几份可在线免费获取优秀资源, 请参阅“参考书目“部分(第1.9节).
一个数学家的辩白. 部分学生可能会好奇为什么这本书包含如此多的数学, 这是因为数学就是一门能够简洁而精确描述概念的语言. 在这本书中, 我们使用数学来描述计算的概念. 比如说, 我们将思考诸如“是否存在一种高效算法来求取给定整数的质因数?“这样的问题(我们将看到这个问题尤为有趣, 它甚至触及了从互联网安全到量子力学等跨度极大的问题! )若要精准的描述这些问题, 我们需要对算法这一概念以及算法的高效性给出精准的定义. 此外, 由于无法通过实验证明某种算法不存在, 唯一能证实算法不存在性的方式就是数学证明.
1.1 本章: 读者的参考手册
基于你已有的数学背景, 你有两种阅读本章的方式:
- 如果你已经学习过“离散数学“、“计算机科学中的数学“或任何类似课程, 则无需阅读整章内容, 只需要快速地阅读第1.2节来了解我们会用到什么数学工具与第1.7节来了解本书所用符号, 便可跳转至后续章节. 或者, 你也可以放松心情通读本章, 既熟悉本书所用的符号体系, 顺便品味(或忍受)笔者融于字里行间的哲学思考与幽默尝试.
- 若相关基础较为薄弱, 可以参考第1.9节中提供的学习资源. 本章虽然已经涵盖了所有所需知识点, 但系统性地学习相关知识点可能对你更有帮助. 数学学习重在实践, 通过独立完成练习才能真正掌握这些内容.
- 建议你同时开始回顾离散概率论的相关知识, 本书后续章节(见第18章)将涉及这部分内容.
1.2 前置数学知识的概览
我们将使用的主要数学概念如下所示. 此处仅列出这些概念, 其具体定义将在本章后续部分给出. 若您已熟悉所有这些内容, 可以直接跳至第1.7节查看我们使用的完整符号列表.
- 证明: 最重要的是, 本书包含大量形式化数学推理, 涵盖数学定义、陈述与证明.
- 集合及集合运算: 我们将广泛使用数学集合. 涉及到的集合关系包括属于(与包含( 以及集合运算, 主要是并集(、交集(与差集(
- 笛卡尔积(Cartesian product)与克林星号(Kleene star)运算: 两个集合与的笛卡尔积, 记作(即由所有满足且的所有有序对构成的集合), 表示阶笛卡尔积(例如 而(称为 克林星号 )表示所有对应的的并集.
- 函数: 函数的定义域和陪域, 以及函数的性质(如单射函数和满射函数), 还有部分函数(即不同于全函数的, 对于定义域内部分元素可能存在未定义情况的函数).
- 逻辑运算: 常用操作包括逻辑与(、逻辑或(、逻辑非(等, 以及存在量词(和全称量词(
- 基础组合数学: 诸如(表示大小为的集合中所有元子集的数量)等概念.
- 图论: 无向图和有向图、连通性、路径和环.
- 大表示法: 使用符号分析函数的渐进增长性.
- 离散概率: 我们将使用概率论, 特别是基于有限概率空间(如抛掷枚硬币)的概率论, 包括随机变量、期望和浓度等概念. 概率论仅在本书后半部分使用, 我们将在第18章先行复习. 然而概率推理是一项精妙(且极其实用)的技能, 尽早开始掌握总是有益的.
本章后续部分将简要回顾上述概念. 既是为了帮助读者重温可能已经生疏的知识, 也是为了介绍我们的符号与约定——这些约定有时可能与你之前接触过的版本有所不同.
1.3 阅读数学文本
数学家使用各种专业术语的原因, 与工程、法律、医学等其他众多领域并无差别: 我们需要精确的术语, 并为频繁使用的概念引入简洁表达. 数学文本往往在单个句子中蕴含极高的信息密度, 因此关键在于缓慢而仔细地阅读, 逐个符号解析.
随着练习时间逐渐增长, 你将发现阅读数学文本变得越来越轻松, 且专业术语也不再是问题. 更重要的是, 数学文本阅读能力是从本书中能够获得的极具迁移价值的技能之一. 我们的世界正飞速变化——这不仅体现在技术领域, 更延伸至医学、经济学、法律乃至文化等人类实践的方方面面. 无论你未来方向如何, 都很可能会接触到包含前所未见新概念的文本(参见图 1.1与图 1.2中两个当代“热点领域“的例子). 掌握内化并应用新定义的能力至关重要. 在数学课程相对安全稳定的学习环境中, 这种技能更容易被掌握——至少你可以确信所有概念都有完整定义, 并能随时向教学人员答疑解惑.

图 1.1. 摘自Silver等人2017年发表于《自然》期刊的《AlphaGo Zero》论文“方法“部分片段.

图 1.2. 摘自Ben-Sasson等人奠定加密货币Zcash项目基础的《Zerocash》论文片段.
数学文本的基本构成要素有三: 定义 、断言 与 证明.
1.3.1 定义
数学家经常在已有的概念上定义新的概念. 比如, 以下是一个你可能曾经见过的数学定义(并且我们很快还会再见到):
定义 1.1阐述了一个简单的概念, 但即便如此它也使用了大量符号. 阅读此类定义时, 一边阅读一边用笔进行标注往往很有帮助(见图 1.3). 例如当看到诸如、或等符号时, 务必确认其指代的对象的类别: 是集合、函数、元素、数字, 还是小妖怪? 你可能还会发现, 向朋友(或对自己)用语言解释这一定义会很有帮助.

图 1.3. 定义 1.1的注释版本, 标出了定义的每个对象及其关联的定义
1.3.2 断言: 定理、引理、主张
定理、引理、断言等都是对已定义概念的真命题. 将特定命题称为“定理“、“引理“还是“断言“属于主观判断, 并不改变其数学实质——三者均指代已被证明为真的命题. 区别在于: 定理指代值得铭记和强调的重要结论; 引理通常指技术性结论, 其自身未必重要但能有效辅助其他定理的证明; 断言则是为证明更重大结论而使用的“过渡性“命题, 其自身价值并不受关注.
1.3.1 证明
数学证明是用以证实定理、引理及断言真实性的论证过程. 我们将在下文1.5节讨论证明, 其核心在于数学证明的标准极为严苛. 与其他领域不同, 数学证明必须是“无懈可击“的论证, 确保证明对象无可置疑为真. 本节涉及的数学证明示例参见练习 1.1及1.6节. 如前言所述, 总体而言: 理解定义比掌握定理更重要, 理解定理陈述比掌握其证明过程更重要.
1.4 基础离散数学对象
在本节中, 我们将快速回顾本书中所用的一些数学对象(你当然也可以把这些叫做数学中的“基本数据结构“).
1.4.1 集合
一个集合是一些对象的无序容器. 例如, 表示指代一个包含数字、、的集合(我们使用来表示是中的一个元素. )注意集合与是相同的, 因为它们拥有相同的元素. 同时, 一个集合要么包含一个元素, 要么不包含一个元素, 不存在“包含两次“的概念, 因此我们甚至可以将同一个集合写作(尽管这样写有些奇怪). 有限集合的 基数 (cardinality), 即一个集合包含的元素的数量, 记作(基数亦可以定义在 无限 集上, 见第1.9节的参考资料). 因此在上例中 若集合的元素都是集合的元素, 则称为的一个子集, 记作(我们亦可以称为的一个超集. )比如, 不包含任何元素的集合称作空集, 写作 如果是的一个子集且不等于 则我们称为的一个真子集, 记作
我们可以通过将其元素全部列出来定义集合, 也可以通过写下集合元素满足的一个条件来定义集合, 例如: 当然, 同一集合有多种表示方式, 我们常会使用直观的记号列出几个示例来说明规则. 例如也可将定义为: 注意集合可以是有限的(如或无限的(如 集合的元素不必是数字, 例如英语元音的集合 或按2010年人口普查的美国百万人口城市集合 集合甚至可以包含其他集合作为元素, 例如所有偶数大小子集构成的集合
集合运算: 集合与的的并集记作 包含所有属于或属于的元素. 交集记作 包含同时属于和的元素. 差集记作(部分文献中记作 包含属于但不属于的元素.
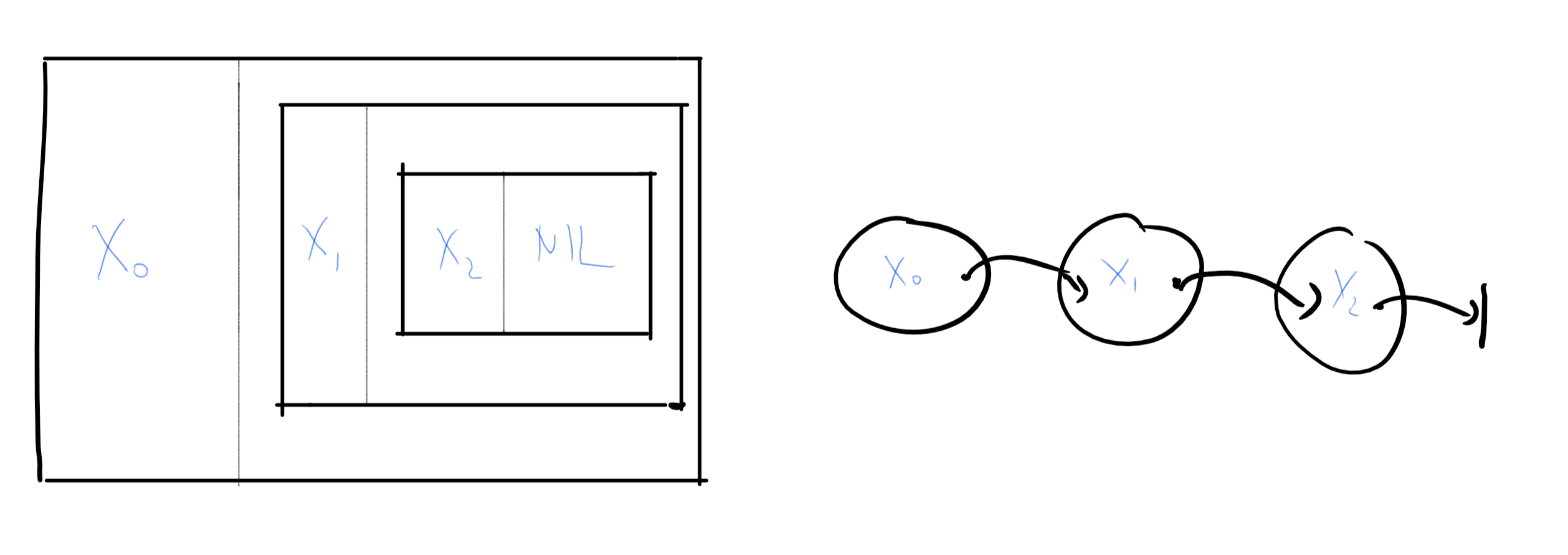
元组、列表、字符串、序列: 元组是有序的对象容器, 例如是包含四个元素的元组(称为-元组或四元组). 由于元组是有序的, 该元组不同于四元组或三元组 -元组亦称为有序对. 术语“元组“与”列表“可互换使用. 若某个元组中的元素均来自于某个有限集(如 则称为字符串. 类比集合, 我们将元组的长度记作 与集合类似, 元组亦有无限形式. 例如由所有完全平方数组成的元组 无限的有序容器称为序列, 有时亦称作“无限序列“以强调这一点. “有限序列“是元组的同义词. (可将集合中元素的序列视为函数(其中对任意满足 类似地, 可将中元素的-元组视为函数 )
笛卡尔积: 若与是集合, 则其笛卡尔积记作 是由所有满足且的有序对构成的集合. 例如, 若且 则包含六个元素: 相似的, 若为集合, 则为由所有满足、、的三元组构成的集合. 更加一般地, 对任意正整数及集合 用表示满足对每个有的有序-元组的集合. 对任意集合 将记作 记作 记作 依此类推.
1.4.2 特殊集合
在本书中会反复用到数个特殊集合. 集合
包含了所有的自然数, 即非负整数. 对于任意的自然数 定义集合为(与均从开始计数, 与此同时诸多文献中这两个集合是从开始的计数的. 从零开始计数只是一个约定俗成的做法, 只要保持一致性, 并不会产生太大差异. )
我们偶尔也会使用集合来表示所有(负的和非负的)整数, 同时使用来表示所有实数(这个集合不仅包含整数, 同时也包含分数与无理数, 例如, 包含诸如、等的数字. )我们使用来表示所有正实数的集合 这个集合有时亦写作
字符串: 另外一个我们经常会用到的集合是 这个集合包含了所有长度为(为任意自然数)的二进制字符串. 换句话说, 是包含所有由组成的-元组的集合. 这与我们前文中的符号一致: 是笛卡尔积 是笛卡尔积 依此类推.
我们将字符串简单地写作 例如, 对于所有字符串与 我们将的第个元素记作
我们也经常会使用包含所有长度二进制字符串的集合, 即 另一个表示这个集合的方式是 或者更为简洁的 集合包含了“长度为的字符串“或“空字符串“, 我们将这个字符串记作(此处我们使用与大部分编程语言一致的符号, 其他文献可能会使用或来表示空字符串).
推广星号操作: 对于任意集合 我们定义 例如, 若 则表示字母表a-z上所有有限长度字符串的集合.
连接操作: 两个字符串与的连接是指将书写在后形成的长度的字符串 具体而言, 若且 则等于满足以下条件的字符串 当时 当时
1.4.3 函数
若与为非空集合, 则从到的函数(记作会将每个元素关联到一个元素 集合称为函数的定义域, 集合称为的陪域. 函数的像是指集合 即由所有被映射的输入元素对应的输出元素组成的的陪域子集(有些文献使用“值域“一词表示函数的像, 而另一些文献使用”值域“表示函数的陪域. 因此我们将完全避免使用“值域“这一术语. )与集合类似, 我们可以通过列出函数对中所有元素给出的取值表或通过规则来定义函数. 例如, 若且 则下表定义了一个函数 注意该函数与规则定义的函数相同.
若满足对所有均有 则称是单射(见定义 1.1, 亦称为单射函数). 若满足对每个均存在某个使得 则称是满射(亦称作满射函数). 既是单射又是满射的函数称为双射函数或双射. 从集合到自身的双射亦称为的排列. 若是双射, 则对于每个均存在唯一的使得 我们将该值记作 注意本身也是从到的双射(你能明白为什么吗? ).
给出两个集合之间的双射通常是证明集合大小相同的有效方法. 事实上, “与具有相同基数“的标准数学定义就是存在一个双射 此外, 若存在从到集合的双射, 则定义集合的基数为 正如我们将在本书后面看到的, 这个定义可以推广到无限集合的基数定义.
部分函数(又译偏函数): 我们有时会关注从到的部分函数. 部分函数允许在的某个子集上未定义. 也就是说, 若是从到的偏函数, 则对每个 要么(如标准函数的情况)存在中的元素 要么未定义. 例如, 部分函数仅定义在非负实数上. 当需要偏函数和标准(即非部分)函数时, 我们称后者为全函数. 当我们不加限定地说“函数“时, 指的是全函数.
部分函数的概念是函数的严格推广, 因此每个函数都是部分函数, 但并非每个部分函数都是函数(也就是说, 对于任意非空集合与 从到的偏函数集合是从到的全函数集合的真超集. )当需要强调从到的函数可能不是全函数时, 我们写作 我们也可以将从到的偏函数视为从到的全函数, 其中是一个特殊的“失败符号“. 因此, 我们可以说 而不是在处未定义.
关于函数的基本事实: 验证能否证明以下结论是复习函数知识的绝佳方式:
- 若和是单射函数, 则它们的复合函数(定义为也是单射.
- 若是单射, 则存在一个满射函数 使得对于每个均有
- 若是满射, 则存在一个单射函数 使得对于每个均有
- 若与是非空有限集合, 则以下条件相互等价: (a) (b) 存在单射函数 (c) 存在满射函数 这些等价关系实际上对无限集合和亦成立. 对于无限集合, 条件(b)(或等价的条件(c))是的公认定义.
暂停思考:
你可以在许多离散数学教材中找到这些结论的证明, 例如Lehman-Leighton-Meyer讲义中的第4.5节. 但我强烈建议你尝试独立证明它们, 或至少通过证明小规模情况(如的特殊实例来确信这些结论成立.
让我们以其中一个事实为例进行证明:
对引理 1.1的证明
对引理 1.1的证明
选择某个 我们将定义函数如下: 对每个 若存在某个使得 则令(由于的单射性质, 不可能有两个不同的同时映射到 因此的选择是无歧义的). 否则, 令 现在对于每个 根据的定义, 若 则 此外, 这也表示是满射, 因为这意味着对每个都存在某个(即使得
1.4.4 图
图在计算机科学及众多其他领域中无处不在. 图可以用于建模非常多的数据类型, 包括但不限于社交网络、调度约束、道路网络、深度神经网络、基因相互作用、观测值之间的相关性. 几种图的正式定义将在下面给出, 但如果你没有在先前的课程中了解过图, 我强烈建议你从第1.9节中的资料中详细了解它们.
图有两种基本类型: 无向图与有向图.
基于这个定义, 我们可以定义关于图与顶点的几个性质. 我们将的相邻节点的个数成为的度数. 图中的一条路径是一个元组(其中 且满足对每个 都是的相邻节点. 简单路径是指所有均不重复的路径 环是指满足的路径 若两个顶点满足或存在一条从到的路径, 则称这两个顶点是联通的. 当图中每对顶点都联通时, 我们称该图是连通图.
下面是一些关于无向图的基本事实. 我们将为它们给出一些非正式的论证, 但完整证明作为练习留待读者自行完成(完整证明可以在第1.9节中的诸多资源中找到).
通过观察可知: 每条边会对度数总和贡献两次(一次作用于 另一次作用于 由此可证明引理 1.2.
通过将路径与路径拼接, 得到连接与的路径 即可证明引理 1.3.
通过“捷径修剪法“可证明引理 1.4: 若某路径中同一节点出现两次, 则移除其间的循环段(见图 1.5). 将这一直观论证转化为形式化证明是很好的练习:
证明引理 1.4.
对练习 1.1的解答
对练习 1.1的解答
此证明遵循图 1.6所示的思路. 需要注意的复杂性在于: 路径中可能有多个顶点被重复访问, 因此“捷径修建“不一定能直接得到简单路径. 我们通过考察与之间的最短路径来解决该问题. 具体如下:
设为无向图, 和为中两个连通顶点. 我们将证明存在连接和的简单路径. 令为与之间路径的最短长度, 并设为一条长度为的路径(可能存在多条此类路径, 若有则任选其一). (即 且对任意有 )我们断言是简单路径. 假设存在某个顶点在路径中出现两次: 即对某些有且 此时可通过取的前个顶点(从到的首次出现)和后个顶点(从第二次出现后的顶点到 得到捷径路径 由于 和都是中的边, 因此是连接和的有效路径. 但的长度为 这与的最小性矛盾.
练习 1.1是寻找证明过程的典型示例. 首先确保理解命题含义, 随后提出非形式化论证说明其成立性, 最后将非形式化论证转化为严格证明. 该证明不必过长或过度形式化, 但应清晰阐述为何从假设可推出结论.
度数和连通性的概念亦可自然推广至有向图, 其定义如下:
有向图可能同时包含边和 此时和互为入邻居和出邻居. 顶点的入度是其入邻居的数量, 出度是其出邻居的数量. 图中的路径是指元组(其中 且对每个有是的出邻居. 与无向图情形类似, 简单路径是指所有均不相同的路径 环是指满足的路径 我们经常关注的一类有向图是有向无环图(Directed Acyclic Graph, DAG), 顾名思义即为不含环的有向图:
上述引理在有向图中均有对应版本. 其证明(与无向图情形基本一致)将作为习题留给读者.
1.4.5 逻辑运算符与量词
如果和是可真可假的陈述, 则与(记为是一个当且仅当和同时为真时才成立的陈述; 而或(记为是一个当且仅当或为真是成立的陈述. 的否定记作或 当且仅当为假时该陈述为真.
假设是一个依赖于某个参数(有时亦称为自由变量)的陈述, 其特性在于: 对于从集合中取值的每一个的具体赋值, 都会有明确的真值. 例如这个陈述本身没有固有真值, 但当我们用具体实数代入时, 它就会成为真或假的命题. 我们用表示这样一个陈述: 当且仅当对所有都有为真时, 该陈述为真. 用表示这样一个陈述: 当且仅当存在某个使得为真时, 该陈述为真.
例如下面这个形式化表达式, 描述的是“存在大于100且不能被3整除的自然数“这个真命题: “对于足够大的”. 本书中会反复出现“某个陈述对于足够大的成立“这样的论断, 其含义是: 存在整数 使得对于所有 都成立. 我们可以将其形式化为
1.4.6 求和与求积的量词
使用下列简记法来表示多个数的求和或求积往往更为便捷. 若是有限集且是函数, 则表示: 表示: 例如, 从到的所有整数的平方和可表示为:
由于对整数区间求和极为常见, 对此存在特殊记号. 对于任意两个满足的整数, 表示 其中 因此(1.1)可改写为:
1.4.7 解析公式: 约束变量与自由变量
在数学中, 如同在编程中一样, 我们常常会遇到符号化的“变量“或“参数“. 给定某个公式时, 理解特定变量在该公式中是约束变量还是自由变量至关重要. 例如在如下陈述中, 是自由变量, 而和是受存在量词约束的变量:
由于是自由变量, 它可以被赋予任意值, 因此(1.2)的真值取决于的取值. 例如当时公式成立, 但当时则不成立. (你能看出原因吗? )
同样的问题在解析代码时也会出现. 例如在下列C语言代码片段中:
for (int i=0 ; i<n ; i=i+1) {
printf("*");
}
变量i在for循环块内是约束变量, 而变量n则是自由变量.
约束变量的主要特性是: 我们可以对其进行重命名(只要新名称不与其他变量名冲突)而不改变语句的含义. 因此以下陈述
与(1.2)完全等价—它们对值的真值判断完全相同.
同样地, 代码:
for (int j=0 ; j<n ; j=j+1) {
printf("*");
}
与使用i的代码段有完全相同的执行效果.
数学符号与编程语言存在诸多相似性, 这源于二者都是为精确传递复杂概念而构建的形式化体系. 但两者存在文化差异: 编程语言通常使用具有实际意义的变量名(如NumberOfVertices), 而数学则倾向于使用简短标识符(如 部分原因可能源于数学证明的传统形式—手写论证与口头阐述, 而非键入代码并编译执行. 另一个原因是: 在证明中使用错误变量名最多导致读者困惑, 但在程序中使用错误变量名则可能导致飞机失事、患者死亡或火箭爆炸.
由此带来的结果是: 数学中常常重复使用标识符, 甚至会耗尽字母表而不得不引入希腊字母, 并通过区分大小写及字体样式来扩展表示范围. 同样地, 数学符号体系大量使用“重载“机制——例如运算符可对应多种不同对象(实数、矩阵、有限域元素等), 其具体含义需通过上下文推断.
两个领域都存在“类型“概念. 在数学中, 我们通常约定特定字母表示特定类型的变量: 例如通常表示整数, 通常表示极小正实数(相关约定详见1.7节). 阅读或撰写数学文本时, 我们无法依赖“编译器“进行类型安全检查, 因此必须密切关注每个变量的类型, 确保所有操作都是“合法“的.
Kun的著作(Kun, 2018)对数学与编程文化的异同进行了深入探讨.
1.4.8 渐近分析与大表示法
精确描述运行时间等量通常非常繁琐, 且并无必要, 因为我们通常主要关注的是“高阶项“. 也就是说, 我们希望理解该量随输入变量增长时的缩放行为. 例如, 就运行时间而言, 一个时间算法与一个时间算法之间的差异, 远比时间算法与算法之间的差异更加显著. 为此, 大表示法作为一种“简化表述“的方式极为有用, 它能让我们的注意力集中在真正重要的内容上. 例如, 使用大表示法, 我们可以说和都简单的属于(可非正式地理解为“在常数因子范围内相同“), 而(可非正式地理解为“远小于”
通常(尽管为非正式表述), 若是两个将自然数映射到非负实数的函数, 则““表示在不考虑常数因子的情况下 而”“表示远小于 其含义是: 无论给乘以多大的常数因子, 只要取足够大的 都会更大(因此, 有时会将写作 如果且 则写作 这可以理解为: 若不考虑常数因子, 与相同. 更形式化地, 我们如下定义大表示法:
在大表示法中使用“匿名函数“通常很方便. 例如, 当我们写这样的语句时, 我们的意思是 其中是定义为的函数. Jim Apsnes的离散数学笔记第七章很好地总结了大表示法; 另可参阅本教程, 以获得更温和且更面向程序员的介绍.
并不表示相等. 在大表示法中使用等号极为常见, 但这种用法其实并不准确, 因为诸如的语句实际上表示属于集合 如果说有什么更合理的表示法, 那就是使用不等式写作和 而将等号保留给 因此, 我们有时也会使用这种表示法, 但由于使用等号的习惯已经根深蒂固, 我们通常也沿用此习惯. (有些文献写作而非 但我们不会使用这种表示法. )尽管等号可能引起误解, 但请记住: 诸如的语句表示在忽略常数的粗略意义上“至多“为 而诸如的语句表示在相同粗略意义上“至少“为
1.4.9 关于大表示法的一些“经验法则“
在比较两个函数和时, 有一些简单的经验法则可供参考:
- 在大表示法中, 乘性常数不影响结果. 因此, 若 则 当两个函数相加时, 我们只需要关注较大着. 例如, 在大表示法的语句下, 与等价. 一般而言, 对于任意多项式, 我们只需关注高阶项.
- 对于任意两个常数 当且仅当时, 成立, 当且仅当时, 成立. 例如, 综合以上两点可知:
- 多项式函数始终小于指数函数: 对于任意两个常数和(即使远小于 都有 例如,
- 类似地, 对数函数始终小于多项式函数: 对于任意两个常数 (记作满足 例如, 综合上述观察可得:
虽然大表示法常用于分析算法的时间复杂度, 但这绝非其唯一用途. 我们可以用大表示法来限定任意两个从整数映射到正数的函数之间的渐近关系. 无论这些函数是衡量运行时间、内存使用量, 还是其他与计算无关的量, 该方法均适用. 以下是一个与本书无关的例子(你可选择跳过): 黎曼猜想(数学领域最著名的未解问题之一)的一种表述方式是: 在到之间的质数数量等于 且其加性误差至多为
1.5 证明
许多人认为数学证明是从若干公理出发, 通过逻辑推导最终得出结论的过程. 事实上, 某些词典也采用这种方式定义证明. 这种理解并非完全错误, 但从本质而言, 对命题X的数学证明实质上是一个能让读者确信X为真且不容置疑的论证过程.
构建此类证明需要做到:
- 精确理解X的含义.
- 使自己确信X为真.
- 用清晰、准确、简洁的书面英语记录推理过程(仅在有助于明确性时使用公式或符号).
多数情况下, 第一步最为关键. 理解命题含义往往比理解其真理性更耗费心力. 在第三步中, 为使读者毫无疑虑, 我们常需将推理分解为若干“基本步骤“, 其中每个步骤都应简单到“不言自明“的程度——所有步骤的叠加最终导出目标命题.
1.5.1 证明与程序
证明写作与程序编写具有高度相似性, 且二者所需的技能也高度重合. 程序编写包含:
- 理解程序需要实现的功能.
- 确信该功能可通过计算机实现(可通过在白板或记事本上规划如何拆解为子任务来实现).
- 将规划转化为编译器或解释器可读的代码(通过将每个任务拆解为某种编程语言的基本操作序列).
- 与证明过程类似, 程序设计的第一步往往最为关键. 核心区别在于: 证明的阅读者是人类, 而程序的阅读者是计算机(随着机器可验证证明形式的普及, 这种差异正在逐渐消弭; 此外, 为确保程序的正确性与可维护性, 人类可读性至关重要). 因此我们特别强调证明的逻辑流畅性与可读性(这对程序编写同样重要). 撰写证明时, 应假想读者是聪明但极度多疑且挑剔的, 他们会对任何未充分论证的步骤提出质疑.
1.5.2 证明的书写风格
数学证明是一种特定类型的写作形式, 具有独特的惯例与偏好风格. 如同所有写作类型, 熟能生巧, 且通过修改草稿提升清晰度至关重要.
在命题的证明中, “ 证明: “与” 证毕 “之间的所有文字都应专注于论证的真实性. 题外话、示例或沉思应置于这两个标记之外, 以免造成读者困惑. 证明应具备清晰的逻辑流: 每个句子或公式都应有明确目的, 且读者能清晰理解其作用. 撰写证明时, 应对每个句子或公式进行审视:
- 该句子/公式是否在声明某个命题为真?
- 若是, 该命题是从前述步骤推导而来, 还是将在后续步骤中建立?
- 这个句子/公式起什么作用? 是通向原命题证明的一步, 还是为证明先前所述的中间论断而设?
- 最后, 读者是否能清晰理解前三个问题的答案? 若否, 则需要调整顺序、重新表述或补充说明.
关于数学写作的推荐资源包括Lee的讲义、Hutching的讲义, 以及斯坦福大学CS103课程中的若干优秀讲义.
1.5.3 证明的方法
正如编程一样, 证明亦有数种常用的方法. 以下是一些例子:
反证法: 证明的一种方式是展示, 若为假, 则会导致导出矛盾. 这种类型的证明通常由一句“假设, 为了得出矛盾, 为假“作为开头, 并以推导出一个矛盾作为结尾(如违反定理陈述中的某个假设). 以下是一个例子:
引理 1.8.
不存在自然数使得
证明
证明
假设, 为了得出矛盾, 上述引理为假. 令为满足的最小自然数(其中 对此等式两侧平方有 即 此式表明为偶数. 由于两个奇数之积亦为奇数, 这表明必须是偶数, 即存在使得 将此式代入有 即 且这表明亦为为偶数. 与类似, 我们亦可得到为偶数. 因此, 与为两个满足的自然数, 这与的最小性相矛盾.
全称命题的证明: 我们经常需要证明形如“所有类型为的对象都具有性质“的命题 这类证明通常以“设为类型的一个对象“开始, 并通过证明具有性质来结束, 以下是一个简单的例子:
引理 1.9.
对于任意自然数 和中必有一个是偶数.
蕴含命题的证明: 另一种常见情况是命题形如“蕴含“. 这类证明通常以“假设成立“开始, 并通过从导出来结束. 以下是一个简单的例子:
引理 1.10.
如果 则二次方程有解.
证明
证明
证明: 假设 则是一个非负数, 因此存在平方根 于是满足:
整理(1.4), 我们得到:
等价命题的证明: 如果命题形如“当且仅当“(通常简写为” iff “), 那么我们需要同时证明蕴含和蕴含 我们将蕴含的方向称为“仅当“方向, 将蕴含的方向称为“当“方向.
通过中间结论组合的证明: 当证明较为复杂时, 将其分解为多个步骤通常是有帮助的. 也就是说, 为了证明命题 我们可能先证明命题、和 然后证明蕴含 (注: 表示逻辑与运算符. )
分情况证明: 这是上述方法的一种特殊形式, 即为了证明命题 我们将其分为若干情况 并证明: (a) 这些情况是穷尽的, 即其中一种情况必须发生; (b) 逐一证明每种情况都能推导出我们想要的结果
数学归纳法证明: 我们将在下面的第1.6.1节中讨论数学归纳法并给出示例. 我们可以将这类证明视为上述方法的变体, 其中我们有无穷多个中间结论 并证明成立, 且蕴含 蕴含 依此类推. 卡内基梅隆大学15-251课程的网站提供了一份有用的讲义, 介绍了使用数学归纳法时可能遇到的常见陷阱.
“不失一般性”(without loss of generality, w.l.o.g): 这个术语最初可能令人困惑. 它本质上是一种通过简化情况分析来简化证明的方法. 其思想是, 如果情况1和情况2在变量替换或类似变换下是相同的, 那么情况1的证明也隐含了情况2的证明. 但对此应始终保持怀疑态度. 每当在证明中看到它时, 问问自己是否理解为什么所做的假设是真正“不失一般性“的; 而当使用它时, 尝试确认这种使用是否确实合理. 在撰写证明时, 有时最简单的方法是直接重复第二种情况的证明(并添加注释说明该证明与第一种情况非常相似).
数学证明最终是用英文散文写的. 知名计算机科学家Leslie Lamport认为这是一个问题, 证明应该以更形式化和严谨的方式书写. 他在手稿中提出了一种结构化分层证明的方法, 其形式如下:
- 对于形如“如果则“的命题, 其证明是一系列编号的声明, 以假设成立开始, 并以声明成立结束.
- 每个声明后面都附有一个证明, 展示它如何从先前的假设或声明推导出来.
- 每个声明的证明本身又是一系列子声明.
Lamport格式的优点在于, 证明中每个句子的作用非常清晰. 此外, 这种证明也更容易转换为机器可检查的形式. 缺点在于, 这类证明可能读起来和写起来都很繁琐, 且论证的重要部分与常规部分之间的区分不够明显.
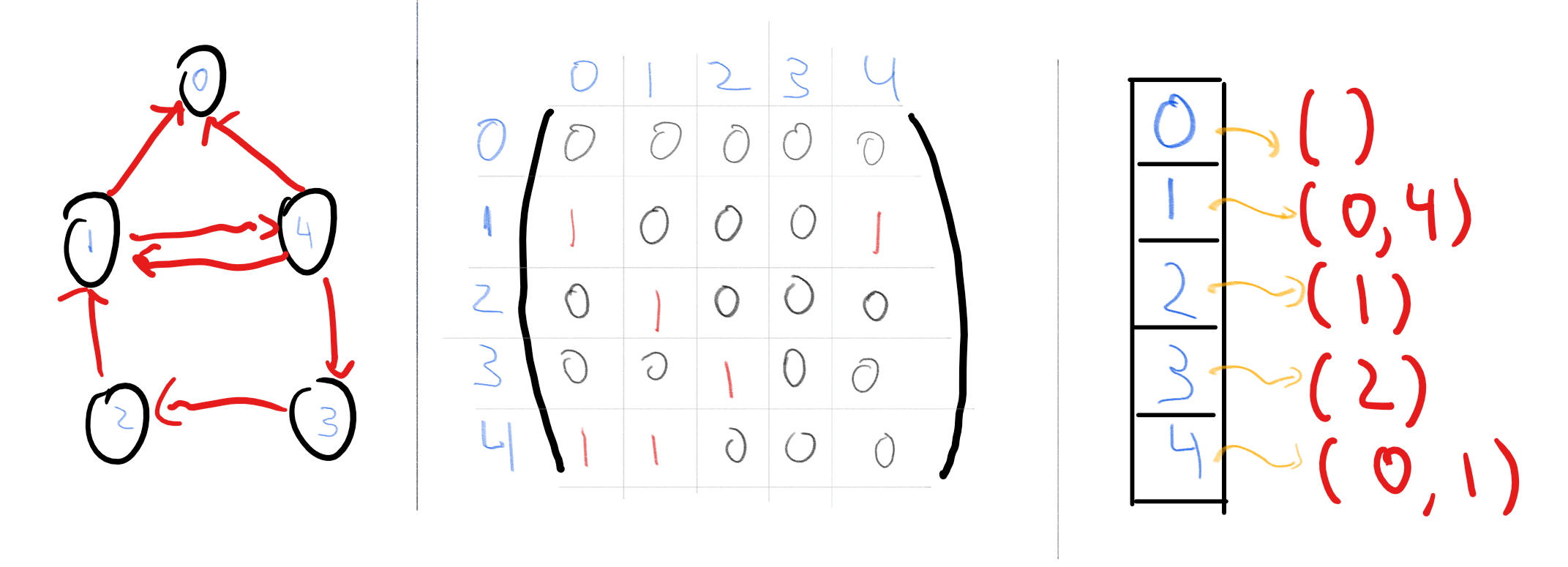
1.6 扩展示例: 拓扑排序
在本节中, 我们将证明如下结论: 每个有向无环图(DAG, 参见定义 1.4)都可以进行分层排列, 使得对于所有有向边 顶点所在的层都大于所在的层. 这一结论被称为拓扑排序, 被广泛应用于任务调度、构建系统、软件包管理、电子表格单元格计算等场景(见图 1.7). 事实上, 在本书后续内容中我们也会用到这一结论.
我们首先给出如下定义. 有向图的分层是指为每个顶点分配一个自然数(对应其所在层)的方法, 要求的入邻居处在更低编号的层, 而出邻居处于更高编号的层. 形式化定义如下:
本节将证明: 有向图是无环的当且仅当其存在有效分层.
要证明此类定理, 首先需要理解其含义. 由于这是一个“当且仅当“类型的陈述, 定理 1.1对应两个命题:
要证明定理 1.1, 则需同时证明引理 1.11和引理 1.12. 引理 1.12的证明实际上并不困难: 直观上, 若包含环, 则环上所有边的层数不可能全程递增—因为沿着环行进时必然会回到起点. 形式化证明如下:
引理 1.11对应着更复杂(但更有用)的方向. 要证明它, 需要说明如何为任意有向无环图构造分层, 使得所有边“指向上层“.
暂停思考:
若未曾见过该定理的证明(或者已经遗忘), 此时建议暂停阅读并尝试自行证明. 一种思路是描述算法: 输入为具有个顶点和不超过条边的有向无环图 输出长度为的数组 使得对于图中每条边都有
1.6.1 数学归纳法
证明引理 1.11存在多种方法. 一种做法是: 首先针对小型图(如具有1、2或3个顶点的图, 参见图 1.8进行证明——这类有限情形可通过穷举法验证, 随后尝试将证明推广至更大规模的图. 这种证明方法的技术术语称为归纳证明.
归纳法本质上是显而易见的“肯定前件“逻辑规则(Modus Ponens)的应用, 该规则指出: 若(a) 命题为真, 且(b) 蕴含 则为真.
在归纳证明的框架中, 我们通常有一个由整数参数化的命题 并通过证明以下两点来完成: (a) 为真; (b) 对任意 若均为真, 则为真(尽管证明(b)通常是难点, 但也存在需要巧妙处理“基础情形“(a)的案例). 通过运用肯定前件规则, 我们可以从(a)和(b)推导出为真. 继而基于与为真的事实, 结合(b)再次运用肯定前件规则可推出为真. 如此循环往复, 可证得对所有均有为真. 其中(a)称为“基础情形“, (b)称为“归纳步骤“, (b)中假设对成立的条件称为“归纳假设“(此处描述的归纳形式有时被称为“强归纳法“, 以区别于“弱归纳法“——后者将(b)替换为“若为真则为真“; 弱归纳法可视为强归纳法的特例, 即不要求使用为真的条件).
归纳证明与递归算法密切相关. 两者都是通过将大规模问题转化为较小规模的同类实例来求解. 在解决输入规模为的问题时, 递归算法会预设“若已获得解决规模小于的问题实例的方法“; 而在证明参数为的命题时, 归纳法会思考“若已知对任意均有为真“.
归纳与递归都是本课程及计算机科学领域(甚至数学与其他科学领域)的核心概念. 初学者可能会感到困惑, 但随着实践积累将会逐渐理解. 若需进一步了解归纳证明与递归, 可参考斯坦福大学CS103课程讲义、MIT 6.00课程讲座或Lehman-Leighton专著节选.
1.6.2 通过归纳证明结论
通过归纳法证明引理 1.11有多种方式. 我们将基于顶点数量进行归纳, 因此定义命题如下:
表示: “对于每个具有个顶点的有向无环图 都存在对的分层赋值. “
当(即图不含顶点)时命题显然成立. 因此只需证明: 对于每个 若成立则成立.
为此, 我们需要找到一种方法: 给定具有个顶点的图 将寻找分层的问题转化为寻找具有个顶点的其他图的分层问题. 核心思路是找到的一个源点(即没有入边的顶点 随后将顶点分配至0层, 并依据归纳假设将剩余顶点分配至等层.
以上是引理 1.11证明的直观思路. 但在撰写正式证明时, 我们将基于后见之明进行优化, 将原本曲折的推理过程转化为从“证明: “开始到“证毕(QED1)”(或符号结束的线性化逻辑流. 讨论、示例和旁注虽颇具启发性, 但应该置于这两个标记界定的空间之外——正如优秀的指南所述, 此空间内“每个句子都必须承担论证功能“. 如同编程, 我们可以将证明分解为小型“子程序“或“函数“(数学中称为引理或断言), 即通过辅助性小命题来证明主要结论. 但证明结构必须确保读者能清晰把握论证阶段, 理解每个句子的作用及所属部分. 现正式证明引理 1.11.
对引理 1.11的证明
对引理 1.11的证明
证明: 设为有向无环图, 为其顶点数. 采用对归纳法证明. 基础情形时命题显然成立. 当时, 归纳假设为: 所有顶点数不超过的有向无环图均存在分层.
首先建立如下断言:
断言: 图必存在入度为零的顶点
断言证明: 假设反之, 即每个顶点都有入邻居. 任取顶点 令为的入邻点, 为的入邻点, 依此重复步构造序列 其中每个都有是的入邻点(即存在边 由于图仅含个顶点, 该序列的个顶点中必存在重复, 即存在使得 此时序列构成环, 与有向无环图假设矛盾. (断言证毕)
根据该断言, 取为中某个入度为零的顶点, 令为移除后得到的图. 含个顶点, 由归纳假设存在分层函数 定义函数如下:
需证是有效的分层赋值, 即对任意边满足 分情形讨论:
- 情形1: 且 此时边存在于中, 由归纳假设有 故
- 情形2: 且 此时 而
- 情形3: 且 此情形不可能发生, 因为没有入邻居.
- 情形4: 且 此情形亦不可能, 因这意味着存在自环(属于有向无环图禁止的环结构).
故是的有效分层赋值, 证明完成.
暂停思考:
阅读证明的能力与构造证明同样重要. 事实上, 如同理解代码, 这本身就是一项高阶技能. 建议重读上述证明, 逐句思考: 其假设是否合理? 该句是否真正达成了论证目标? 另一个好习惯是在阅读时对每个变量(如上述证明中的、、、等)思考以下问题: (1)变量类型是什么(数字/图/顶点/函数? ); (2)已知信息有什么(是否为集合的任意元素? 是否已证明其某些性质? ); (3)试图论证的目标是什么?
1.6.3 最小性和唯一性
定理 1.1保证每个有向无环图都存在分层函数 但这种分层不一定唯一. 例如, 若是图的有效分层, 那么定义为的函数也是有效分层. 然而最小分层却是唯一的——最小分层要求每个顶点都被赋予尽可能小的层数. 现正式定义最小性并陈述唯一性定理:
定理 1.2中的最小性定义意味着: 对每个顶点 我们无法在保持分层有效性的前提下将其移至更低层. 若是源点(即入度为零), 则最小分层必须将其置于层; 对于其他顶点 若 则由于存在满足的入邻居 我们无法将修改为或更小值. 定理 1.2表明最小分层是唯一的, 即任何其他最小分层都与完全相同.
证明思路: 对层数进行归纳. 若和都是最小分层, 则它们必然在源点处取值一致(因为都必须将源点分配至层). 接着可证明: 若和在第层及以下取值一致, 则最小性性质要求它们在第层也必须一致. 实际证明中使用了一个简化表述的技巧: 不直接证明(即对每个有 而是证明较弱的命题—对每个有(该条件弱于相等条件, 因为必然蕴含 由于和只是两个最小分层的标注符号, 通过互换符号标签即可用相同证明得到对每个有 从而证得
对定理 1.2的证明
对定理 1.2的证明
设为有向无环图, 是其两个最小有效分层. 我们将通过对的归纳证明: 对每个有 由于除最小性外未对作任何假设, 该证明同样可推出对每个有 故而对每个有 此即所需结论.
当时显然成立: 此时 故至少等于 当时, 根据的最小性, 若则必存在某个入邻居满足 由归纳假设得 而由于是有效分层, 必有 这意味着
暂停思考:
定理 1.2的证明虽然完全严谨, 但表述较为简练. 请务必仔细阅读并理解为何这是一个无懈可击的证明.
1.7 本书所用到的符号及规范
本书采用的大部分符号标记均为数学文本中的通用规范, 主要差异点如下:
- 自然数集的索引从开始(尽管许多计算机科学领域的文献亦采用相同约定)
- 集合的索引从开始, 因此其定义为(其他文献常定义为 类似地, 字符串索引也从开始, 故字符串写作
- 若为自然数, 则不表示数字 而是长度为的字符串(即连续个“1“). 同理, 表示长度为的字符串
- 部分函数未必在所有输入上都有定义. 符号默认表示全函数, 若需强调函数为部分函数时, 将采用的写法
- 本课程主要将计算问题描述为计算布尔函数 而其他教材常采用判定语言的表述. 这两种视角具有等价性: 对于任意集合 存在对应函数满足当且仅当 计算部分函数对应文献中的“承诺问题“(promise problem). 鉴于语言表述在其他教材中更加常见, 我们将适时提醒读者注意这种对应关系
- 使用和分别表示向上取整和向下取整函数, 表示除以的余数(即 在需要整数的语境中, 通常默认将数值隐式取整. 例如“长度为的字符串“实际指的长度为(依据惯例采用向上取整, 但多数情况下取整方式不影响结论)
- 遵循计算机科学文献惯例, 默认对数以为底, 即等价于
- 记号是的缩写(即存在常数使得对足够大的满足 类似地, 表示(即存在常数使得对足够大的满足
- 依照数学文献惯例, 通过添加撇号扩展标识符集: 若表示某对象, 则、等表示同类型的其他对象
- 为降低认知负荷, 定理和习题陈述中常使用等整常数. 这类“整齐“常数通常无特殊含义, 仅为任意选取. 例如定理“算法在长度为的输入上计算函数至多需要步“中的数值可视为足够大的任意常数, 实际可用更小的常数证明的界. 同理, 若问题要求证明某量至少为 实际可能存在更小的常数使得该量至少为
1.7.1 变量命名规范
正如编程一样, 数学中充满了各种各样的变量. 当你看到一个变量时, 追踪这个变量所属的类型至关重要(例如整数、字符串、函数、图等). 为了简化这一过程, 我们尝试一致的为特定的类型使用特定的变量. 部分命名规范在本节列出. 这些命名规范并不是无法更改的法则, 有时我们可能会稍微偏离这一规范. 并且, 这些规范并没有取代在声明新变量前明确指出其指代对象的要求.
本书中的变量命名规范:
标识符 通常指代的对象类型 自然数(即集合中的元素) 趋近于的正实数 通常表示上的字符串, 有时也表示数字或其他对象. 我们常将对象与其字符串表示视为同一 图. 顶点集一般表示为 且通常 边集一般表示为 集合 函数. 通常(非绝对)用小写标识符表示有限函数(映射关系为, 常见 无限输入函数, 映射关系为或(为某定值). 根据上下文, 可指函数或图 布尔电路 图灵机 程序 表示时间界限的函数, 映射关系为 正数(常指未明确的常数, 例如表示存在常数使得对所有满足 有时也以来表示此类常数 有限集(通常用于表示字符串集合的字母表)
1.7.2 一些惯用表达
数学文本通常遵循特定惯例或“惯用表达“. 本文使用的一些典型惯用表达包括:
- “设为…”、“令表示…“或“令”: 这些都是在表达指代省略号所代表的内容. 当表示某些对象的属性时我们可能会通过“若…满足…条件, 则称其具有性质“的方式来定义. 虽然我们尽量先定义后使用, 但有时为了语句流畅会在定义前使用术语, 此时会通过“其中指…“的说明来解释前述表达中的含义.
- 量词: 数学文本涉及大量“对于所有“和“存在“等量词. 有时我们会完整拼写为“对于所有“或“存在”, 有时则直接使用符号和 必须注意每个变量的量化方式及其依赖关系. 例如“对于每个 存在“意味着的选择依赖于 量词顺序至关重要: 命题“对每个大于的自然数 都存在质数能整除“为真, 而“存在质数能整除每个大于的自然数“则为假.
- 编号公式、定理、定义: 为便于追溯已定义术语和已证明命题, 我们通常为其添加(数字)标签, 并在文中其他部分引用.
- (i.e.,)与(e.g.,): 数学文本中常见这类拉丁缩写. 当与等价时使用“(i.e., “; 当是的实例时使用”(e.g., “, 如“自然数(i.e., 非负整数)“或“自然数(e.g., 77)”.
- “因此”、“故而”、“可得”: 这些词引导的句子是由前文推导得出的结论, 例如“具有个顶点的图是连通的, 因此它至少包含条边“. 有时使用“实际上“引出的文本来论证前句主张, 如“具有个顶点的图至少包含条边. 实际上这是因为具有连通性. “
- 常数: 在计算机科学中, 我们通常关注算法资源消耗(如运行时间)随某些量(如输入长度)的变化规律. 将不依赖于输入长度的量称为常数, 因此常出现如下表述: “存在常数 使得对任意 算法在长度为的输入上至多运行步. “虽然严格来说“常数“这个限定词并非必要, 但加上它可以强调是与无关的固定值. 有时为降低认知负荷, 我们会直接用10/100/1000等足够大的整数替代 或采用大表示法表述为“算法的时间复杂度为”.
- 需要掌握的基本数学数据结构包括: 数字、集合、元组、字符串、图和函数
- 可通过基础对象定义更复杂的概念, 例如图可通过顶点对集合来定义
- 基于精确定义的对象可表述明确无歧义的命题, 并通过数学证明判定真伪
- 数学证明并非形式化的仪式, 而是认证命题真实性的清晰、严密且无懈可击的论证
- 大表示法是去掉次要细节、聚焦核心数量关系的极佳形式化工具
- 掌握数学概念的唯一途径是在解决问题中实践运用, 预计您需要在本课程学习中反复查阅本章的定义与符号
1.8 习题
习题 1.3. 用文字描述以下语句:
习题 1.9. 证明对于任意有限集 存在个从到的部分函数.
习题 1.10. 假设是一个序列, 满足且对有 用归纳法证明对每个有
习题 1.11. 证明对任意含有100个顶点的无向图 若每个顶点的度数最多为4, 则存在一个至少包含20个顶点的子集 使得中任意两个顶点均不相邻.
习题 1.13. 举例说明一对函数满足和均不成立.
1.9 参考书目
标题“一个数学家的辩白“指的是哈代所著的经典作品(Hardy, 1941). 即便哈代的观点存在谬误, 其著作仍极具阅读价值.
本书所需的数学背景知识可参考众多网络资源. 其中麻省理工学院6.042课程《计算机科学数学》(Lehman, Leighton, Meyer, 2018)的讲义内容极为全面, 课程视频与作业均在线公开. 伯克利CS70课程《离散数学与概率论》同样提供详尽的在线讲义.
离散数学的其他参考资料包括罗森著作(Rosen, 2019)及吉姆·阿斯彭斯的在线教材(Aspens, 2018). 刘易斯与扎克斯(Lewis, Zax, 2019)以及弗莱克的在线著作(Fleck, 2018)对相同内容作了更通俗的阐释. 索洛(Solow, 2014)是证明阅读与写作的优质入门指南. 库恩(Kun, 2018)为具有编程背景的读者撰写了数学导论. 斯坦福CS103课程提供关于数学证明技巧与离散数学的精彩讲义合集.
定义 1.2中“graph“(图)一词由数学家西尔维斯特于1878年参照用于分子可视化的化学图式所创. 需注意该术语与通常表示数据图表(尤其是函数相对于的图像)的“graph“存在语义混淆. 二者可通过以下方式建立关联: 将函数与定义在顶点集上的有向图相关联, 使得对每个 都包含一条从指向的边. 在此构造的有向图中, 集内每个顶点的出度均为 若函数是单射, 则集内每个顶点的入度至多为 若函数是满射, 则集内每个顶点的入度至少为 若是双射, 则集内每个顶点的入度恰好为
卡尔·波默兰斯的引文出自多伦·齐尔伯格的个人主页.
1: QED即拉丁文quod erat demonstrandum“, 意为“这被证明了“
- 计算与表示
计算与表示
“字母表是一项伟大的发明, 使人们能够轻松地储存并学习他人经过艰难努力才获得的知识 —— 也就是说, 可以通过书本学习, 而非通过与真实世界直接且可能痛苦的接触来学习. “
-B.F. Skinner
“这首歌的名字叫作 ‘HADDOCK’S EYES’.” 骑士说道.
“哦, 这就是歌的名字吗? “ 爱丽丝如此问, 努力装作有兴趣.
“不, 你没明白, “ 骑士有些恼火. “这首歌只是名字被 叫作 这个. 这首歌的名字其实是 ‘THE AGED AGED MAN’. “
“那我应该说, ‘这首 歌 被叫做这个’? “ 爱丽丝认真想了想.
“不, 你不该那么说: 那完全是另一回事! 这首 歌 被叫作 ‘WAYS AND MEANS’, 但你知道, 那只是它被 叫作 这个而已! “
“那么, 这首歌究竟 是 什么呢? “ 爱丽丝问道, 此时她已经完全被搞糊涂了.
“我正要说到这点, “ 骑士回答道. “这首歌其实 是 ‘A-SITTING ON A GATE’, 而曲调是我自创的. “
Lewis Carroll, 爱丽丝镜中奇遇
学习目标
- 区分规范与实现, 亦即区分数学函数与算法/程序.
- 将对象表示为字符串(通常由 0 和 1 构成).
- 常见对象(如自然数、向量、列表与图)的表示实例.
- 前缀无关编码.
- Cantor定理: 实数无法被有限长字符串精确表示.
从初步的角度看, 计算 是一个将 输入 映射为 输出 的过程.
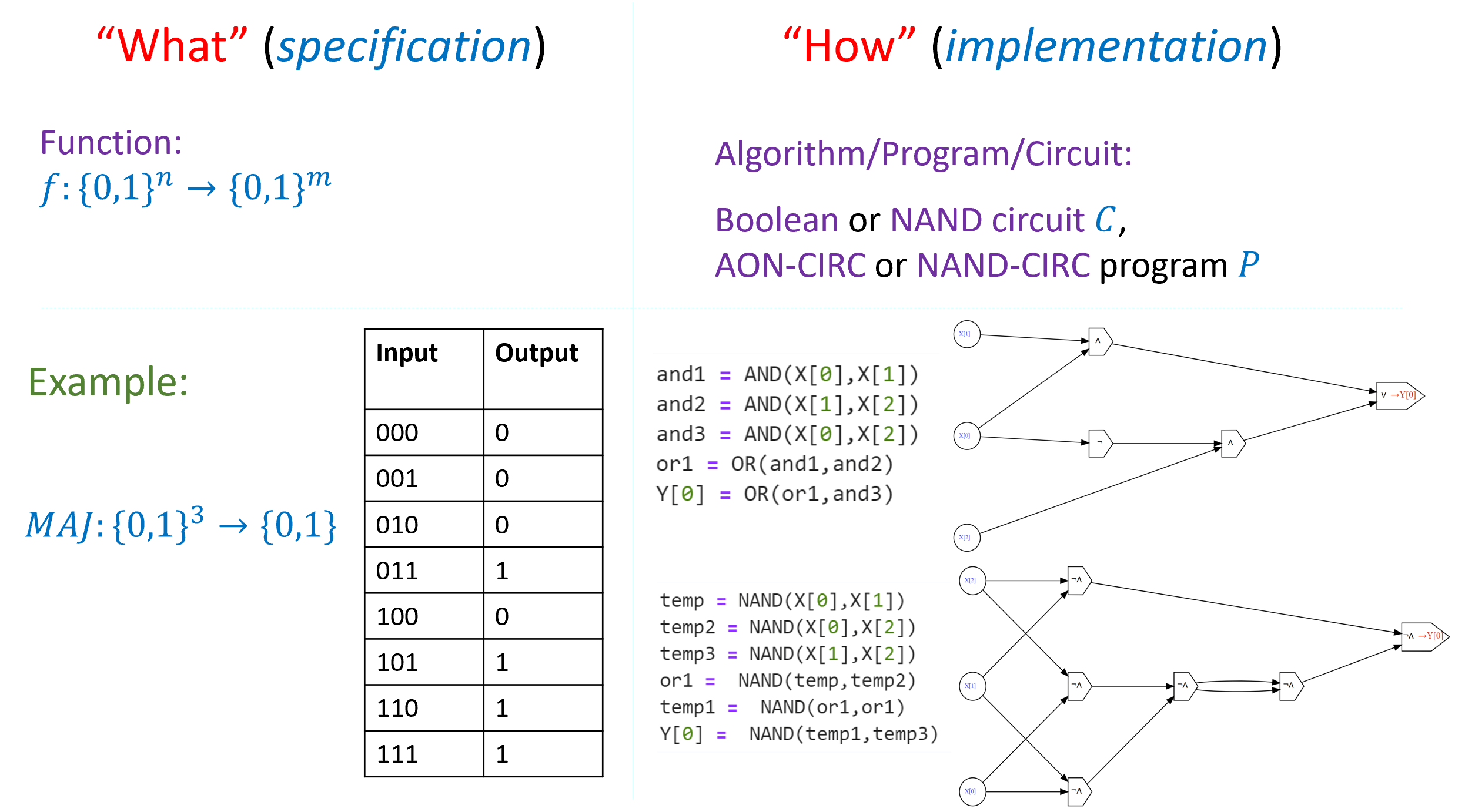
在谈论计算时, 一个关键点是要区分两个问题: 需要完成的任务是什么(即规范), 以及 如何去实现这一任务(即实现方式). 例如, 正如我们已经看到的, 计算两个整数的乘积这一任务, 并不只有唯一的一种实现方式.
在本章中, 我们将聚焦于 “是什么” 部分, 即如何定义计算任务. 而这首先要求我们明确定义 输入与输出. 要囊括所有可能的输入和输出似乎颇具挑战性, 因为如今计算已经被应用在各种各样的对象上, 不仅是数字, 还可以是文本, 图像, 视频, 例如社交网络的连接图, MRI 扫描结果, 基因组数据, 甚至是其它程序.
我们将尝试把所有这些对象表示为 由 0 和 1 组成的字符串, 也就是诸如 或任意有限个 与 组成的序列. (当然, 这样的选择只是出于方便, 0 和 1 并非 “神圣” 而不可替代: 我们完全可以用任何其他有限集合的符号来表示.)
如今, 我们已经对数字化的表示习以为常, 因而并不会对这种编码的存在感到惊讶, 但这实际上是一个深刻的结果, 并带来了许多重要的影响. 许多动物也能够表达某种恐惧或欲望, 但人类独特之处在于 语言: 我们使用有限的一组基本符号来描述潜在无限范围的体验. 语言使得信息能够跨越时间与空间进行传递, 并让社会能够涵盖大量的人群, 随时间积累出共享的知识体系.
在过去的几十年里, 我们见证了一场关于数字化表示与传递的革命: 我们现在几乎可以完美地捕捉视觉与听觉的体验, 并几乎瞬间将其传播给无限的受众. 更重要的是, 一旦信息以数字形式存在, 我们便能够对其进行 计算, 并从中获取以往无法触及的数据洞见. 这场革命的核心, 是一个简单却深刻的观察: 我们能够用有限的一组符号 (事实上仅需两个符号 0 和 1) 来表示无穷多样的对象.
在后续的章节中, 我们通常会默认这种表示方法的存在, 因此会使用诸如 “程序 以 为输入” 这样的表述, 即便 可能是一个数字、向量、图, 或者其他任意对象. 不过我们真正的意思是, 的输入实际上是 的 二进制字符串表示. 在本章中, 我们会更深入地探讨如何构造这样的表示方法.
阅读本章, 我们希望读者能够有以下收获:
-
我们可以使用 二进制字符串 来表示所有我们想作为输入和输出的对象. 例如, 可以利用 二进制基 将整数和有理数表示为二进制字符串 (参见 第2.2.1节 和 第2.2节).
-
我们可以通过 组合 简单对象的表示, 来构造复杂对象的表示. 这样一来, 就可以表示整数或有理数的列表, 并进一步用来表示矩阵、图像和图等对象. 前缀无关编码 (prefix-free encoding) 是实现这种组合的一种方式 (参见 第2.5.2节).
-
一个 计算任务 指定了从输入到输出的映射 – 即一个 函数. 区分 “what” 与 “how”, 或者说 规范 (specification) 与 实现 (implementation), 至关重要 (参见 第2.6.1节). 一个函数仅仅定义了哪个输入对应哪个输出, 而并没有规定 如何 从输入计算出输出. 正如我们在乘法的例子中所看到的, 计算同一个函数可能存在多种方式.
-
虽然所有可能的二进制字符串的集合是无限的, 它仍然无法表示 一切. 特别地, 并不存在将 实数 (绝对精确地) 表示为二进制字符串的方法. 这一结果也被称为 Cantor定理 (Cantor’s Theorem) (参见 第2.4节), 通常表述为 “实数是不可数的”. 这也暗示了无限还存在 不同的层次, 不过在本书中我们不会深入讨论这一话题 (参见 备注 2.3).
本章讨论的两个 “核心思想” 是: 重要提示 2.1 – 我们可以通过组合简单对象的表示来表示更复杂的对象; 以及 重要提示 2.2 – 区分 函数 的 “what” 与 程序 的 “how” 至关重要. 后者将是本书中反复提到的一个主题.
2.1 定义表示
每当我们在计算机中存储数字、图像、声音、数据库或其他对象时, 实际上存储在计算机内存中的只是这些对象的 表示.
此外, “表示” 的概念并不限于电子计算机, 当我们写下文字或画一幅图时, 我们同样是在将思想或体验 表示 为符号序列 (这些符号也完全可以是由 0 和 1 构成的字符串), 甚至我们的脑中也并非储存真实的感官输入, 而是仅仅存储它们的 表示.
为了在计算中使用数字、图像、图或其他对象作为输入, 我们需要精确定义如何将这些对象表示为二进制字符串.
一个 表示方案 (representation scheme) 就是将对象 映射到一个二进制字符串 的方法, 例如, 自然数的一个表示方案就是一个函数
当然, 我们不能把所有的数字都表示成相同的字符串 (比如 “”), 一个最基本的要求是, 如果两个数 和 不同, 那么它们必须被表示为不同的字符串, 换句话说, 我们要求编码函数 是 一一对应 的 (one-to-one).
2.1.1 表示自然数
现在我们来展示如何将自然数表示为二进制字符串.
多年来, 人们已经尝试了各种方式来表示数字, 包括绳结计数, 雅玛数字, 罗马数字, 我们熟悉的十进制, 以及许多其它方法. 我们当然可以使用其中任意一种将一个数字表示为字符串 (参见 图 2.3), 然而, 出于计算上的方便, 我们采用 二进制基 作为默认的自然数字符串表示法.
例如, 我们将数字 6 表示为字符串 因为
类似地, 我们将数字 35 表示为字符串 它满足
更多示例见下表.

图 2.3. 将数字 0, 1, 2, …, 9 的每个数字表示为一个 12×8 的位图图像, 该图像可以被视为属于 的一个字符串. 使用这个方案, 我们可以把具有 位十进制数字的自然数 表示为属于 的一个字符串. 图片来源: A. C. Andersen 的博客文章.
| 十进制表示 | 二进制表示 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 5 | 101 |
| 16 | 10000 |
| 40 | 101000 |
| 53 | 110101 |
| 389 | 110000101 |
| 3750 | 111010100110 |
表格: 使用二进制基表示数字. 左列包含自然数在十进制下的表示, 右列包含相同数字在二进制下的表示.
如果 是偶数, 那么 的二进制表示的最低有效位为 如果 是奇数, 那么该位为
就像数字 对应于“去掉“最低有效的十进制位 (例如, 数字 对应于“去掉“最低有效的 二进制 位.
因此, 二进制表示可以形式化定义为以下函数 ( 表示 “natural numbers to strings”):
其中, 是函数, 定义为: 如果 为偶数, 则 如果 为奇数, 则
像往常一样, 对于字符串 表示字符串 与 的连接.
函数 是 递归定义 的: 对于每个 我们通过较小的数字 的表示来定义
同样, 也可以用非递归方式定义 参见 习题 2.2.
在本书的大部分内容中, 将数字表示为二进制字符串的具体选择并不重要: 我们只需要知道这样的表示是存在的.
事实上, 对于许多用途, 我们甚至可以使用更简单的表示方法, 将自然数 映射为长度为 的全零字符串
备注 2.1 (二进制表示的Python实现 (选读)). 我们可以在 Python 中实现如下的二进制表示:
def NtS(n):# 自然数(Natural number) to 字符串(String)
if n > 1:
return NtS(n // 2) + str(n % 2)
else:
return str(n % 2)
print(NtS(236))
# 11101100
print(NtS(19))
# 10011
我们一样可以使用 Python 实现逆向的转换: 将一个字符串映射回它表示的自然数.
def StN(x):# 字符串 to 自然数
k = len(x)-1
return sum(int(x[i])*(2**(k-i)) for i in range(k+1))
print(StN(NtS(236)))
# 236
2.1.2 表示的意义(讨论)
初学时, 我们自然会认为 是“实际“的数字, 而 只是它的表示.
然而, 对于中世纪的大多数欧洲人来说, CCXXXVI 才是“实际“的数字, 而 (如果他们甚至听说过的话)则是奇怪的印度-阿拉伯位置记数法表示. 1
或许未来当我们的 AI 机器人统治者出现时, 它们可能会认为 才是“实际“的数字, 而 只是它们在向人类下达命令时需要使用的表示方法.
那么, 什么才是“实际“的数字呢? 这是数学哲学家们自古以来一直思考的问题.
柏拉图认为, 数学对象存在于某种理想的存在领域中 (在某种程度上比我们通过感官感知的世界更“真实“, 因为后者不过是理想领域的影子).
在柏拉图的视角中, 符号 仅仅是某个理想对象的记号, 为了向 已故音乐家 致敬, 我们可以称之为 “通常由 表示的数字”.
而奥地利哲学家路德维希·维特根斯坦则认为, 数学对象根本不存在, 唯一存在的只有构成 、 或 CCXXXVI 的实际纸上符号.
在维特根斯坦看来, 数学仅仅是对没有固有意义的符号进行形式操作.
你可以将“实际“的数字理解为(有些递归地)“、 和 CCXXXVI 以及所有旨在表示同一对象的过去和未来的表示方式共同指向的那个东西”.
阅读本书时, 你可以自由选择自己的数学哲学, 只要你能区分数学对象本身与表示它们的各种具体方式, 无论是墨迹斑点、屏幕上的像素、零和一, 还是任何其他形式.
2.2 自然数以外对象的表示
我们已经看到, 自然数可以表示为二进制字符串. 而现在我们将展示, 这对于其他类型的对象也同样适用, 包括(可能为负的)整数、有理数、向量、列表、图以及许多其他对象.
在很多情况下, 为一条数据选择“合适的“字符串表示是非常复杂的任务, 寻找“最佳“表示(例如, 最紧凑, 保真度最高, 最易操作、鲁棒性强(抗干扰能力强), 信息量最大等)一直都是研究的热点.
但目前, 我们先专注于展示一些简单的表示方法, 用于将各种对象作为计算的输入和输出.
2.2.1 表示带有负数的全体整数
既然我们可以将自然数表示为字符串, 我们也可以基于此表示 整数 的全集 (即集合 的成员), 只需增加一位用于表示符号.
为了表示一个(可能为负的)数字 我们在自然数 的表示前加上一个比特 若 则 若 则
形式上, 我们将函数 定义如下:
其中, 的定义如 (2.1) 所示.
虽然表示的编码函数必须是一一对应的, 但不必是 满射.
例如, 在上述表示法中, 没有任何数字被表示为空字符串, 但这仍然是有效的表示方法, 因为每个整数都能被唯一地表示为某个字符串.
给定一个字符串 我们如何判断它“应该“表示一个(非负的)自然数还是一个(可能为负的)整数?
更进一步, 即便我们知道 “应该“是一个整数, 我们又如何知道它使用的是哪种表示方案?
事实上, 除非上下文提供该信息, 否则我们不一定知道. (在编程语言中, 编译器或解释器会根据变量的 类型 决定对应变量的比特序列的表示方法.)
我们可以将同一个字符串 视作表示自然数、整数、一段文本、一幅图像, 或者一个绿色的小妖精.
每当我们说类似 “令 为字符串 表示的数字” 这样的句子时, 我们假设固定某种规范表示方案, 比如上文所示的那些.
具体选择哪种表示方案通常无关紧要, 只需要确保在使用时保持一致即可.
2.2.2 补码表示(选读)
第2.2.1节 中使用特定的“符号位“来表示整数的方法被称为 有符号数表示法 (Signed Magnitude Representation), 曾在一些早期计算机中使用.
然而, 二进制补码表示 在实际中更为常见.
整数 在集合 的 二进制补码表示 是长度为 的字符串 定义如下:
其中, 表示数字 的标准二进制表示, 作为长度为 的字符串, 并根据需要用前导零填充.
例如, 如果 则 而
如果 是大于或等于 的负数, 那么 是一个位于 和 之间的数字.
因此, 该数字 的二进制补码表示是长度为 的字符串, 其首位为
换句话说, 我们将一个可能为负的数字 表示为非负数 (参见 图 2.4).
这意味着, 如果两个可能为负的数字 和 不太大 (即 那么我们可以通过将 和 的表示当作非负整数来进行模 加法, 从而得到 的表示.
二进制补码表示的这一特性是其主要优势, 因为根据微处理器的架构, 它们通常可以非常高效地执行模 的算术运算(对于某些 值, 如 32 或 64).
许多系统将检查值是否过大留给程序员, 无论数字大小如何, 系统都会执行这种模运算.
因此, 在某些系统中, 两个大的正数相加可能得到一个 负数 (例如, 将 与 相加可能得到 因为 参见 图 2.4).
2.2.3 有理数及字符串表示对
我们可以通过表示两个数字 和 来表示分数形式的有理数
然而, 仅仅将 和 的表示简单连接起来是行不通的.
例如, 数字 的二进制表示是 数字 的二进制表示是 但将它们简单连接得到的字符串 也可以看作是 的表示 与 的表示 的连接.
因此, 如果使用这种简单连接方式, 我们将无法判断字符串 是表示 还是
我们通过给 字符串对 提供通用表示来解决这个问题.
如果使用纸笔, 我们只需使用一个分隔符号如 将表示数字 和 的一对数字表示为长度为 9 的字符串 “”.
换句话说, 存在一个一一对应的映射 将 字符串对 映射为一个在字母表 上的单个字符串 (即
使用分隔符类似于英语中使用空格和标点来分隔单词.
通过增加少量冗余, 我们可以在数字领域实现同样的效果.
我们可以将三元素集合 映射到三元素集合 并保持一一对应, 从而将长度为 的字符串 编码为长度为 的字符串
我们对有理数的最终表示通过以下步骤组合得到:
- 将一个(可能为负的)有理数表示为一对整数 使得
- 将整数表示为二进制字符串.
- 将步骤 1 和 2 结合, 得到有理数作为字符串对的表示.
- 将 上的字符串对表示为 上的单个字符串.
- 将 上的字符串表示为更长的 字符串.
同样的思想可以用来表示字符串三元组、四元组, 甚至更多, 作为单个字符串.
实际上, 这是一个非常通用的原则的实例, 我们会在计算机科学的理论与实践中反复使用它(例如, 在面向对象编程中):
重复同样的思想, 一旦我们可以表示类型为 的对象, 我们也可以表示这些对象的 列表的列表, 甚至是列表的列表的列表, 如此类推.
当我们讨论 第2.5.2节 中的 前缀无关编码 (prefix free encoding) 时, 我们会再次回到这一点.
2.3 实数的表示
实数集 包含所有正数、负数、分数, 以及像 或 这样的 无理数.
每个实数都可以用有理数近似, 因此我们可以用一个接近 的有理数 来表示实数
例如, 我们可以用 来表示 误差约为 若希望误差更小(例如约 可以使用 以此类推.
实数通过近似有理数来表示是一个可行的表示方案.
然而, 在计算机应用中, 通常更常用 浮点表示法 (参见 图 2.5) 来表示实数.
在浮点表示法中, 我们用一对 表示 其中 和 是某些规定长度的(可能为正或负的)整数, 并且 最接近
浮点表示是 科学计数法 的二进制版本, 即将一个数字 表示为 的近似.
称之为“浮点“是因为可以将 看作指定一串二进制数字, 描述这串数字中“二进制小数点“的位置.
正是浮点表示的使用, 导致许多编程系统中, 表达式 0.1+0.2 的输出为 0.30000000000000004 而不是 0.3.
更多信息可见: 这里, 这里, 这里.
读者可能会(合理地)担心, 浮点表示法(或有理数表示法)只能 近似 表示实数.
在许多(但不是全部)计算应用中, 可以将精度调得足够高, 以至于不会影响最终结果.
但有时我们仍需要谨慎. 事实上, 浮点数错误有时可能造成严重后果.
例如, 浮点舍入误差曾导致美国爱国者导弹未能拦截伊拉克飞毛腿导弹, 造成 28 人死亡 (详细报道), 以及在计算 英国养老金发放金额 时出现过的 1 亿英镑的错误.
2.4 Cantor定理, 可数集, 以及实数的字符串表示
“对于任意一组水果, 我们可以制作的水果沙拉数量总可以比水果数量更多. 如果不是这样, 我们可以给每个沙拉贴上一个不同水果的标签, 最后再考虑这样一个沙拉, 它包含所有未被标签所指的水果, 那么某个水果恰好在这个沙拉的标签中当且仅当它不在其中.”
鉴于浮点数对实数的近似问题, 一个自然的问题是: 是否可以将实数 精确地 表示为字符串.
不幸的是, 下述定理表明这是不可能的:
不存在一一对应的函数 2
可数集. 我们说一个集合 是 可数的, 如果存在一个满射 或者换句话说, 我们可以将 写成序列
由于二进制表示给出了从 到 的满射, 并且两个满射的复合仍然是满射, 集合 是可数的当且仅当存在从 到 的满射.
利用函数的基本性质(见 第1.4.3节), 一个集合可数当且仅当存在从 到 的一一函数.
因此, 我们可以将 定理 2.1 重述如下:
定理 2.2 由 Georg Cantor 于 1874 年证明.
这一结果(以及相关结论)震惊了当时的数学家. 通过证明不存在从 到 (或 的一一映射, Cantor 展示了这两个无限集合有“不同的无限形式“, 并且实数集 在某种意义上比无限集合 “更大”.
“无限的层次“这一概念当时让数学家和哲学家深感困惑. 哲学家 Ludwig Wittgenstein(前面提到过)称 Cantor 的结果为“完全的胡扯“且“可笑”, 其他人甚至认为更糟: Leopold Kronecker 称 Cantor 是“腐蚀青年的人“, 而 Henri Poincaré 说 Cantor 的思想“应从数学中彻底剔除“.
不过事实证明 Cantor 看得更远. 如今 Cantor 的工作已被普遍接受为集合论和数学基础的基石.
正如 David Hilbert 在 1925 年所说, “无人能将我们从 Cantor 为我们创造的天堂中驱逐出去”.
也正如我们稍后将在本书中看到的, Cantor 的思想在计算理论中也起着重要作用.
我们已经讨论了 定理 2.1 的重要性, 让我们来看看它的证明. 这将分两步进行:
- 定义一个无限集合 对于它证明不可数更加容易(即证明不存在从 到 的一一函数更容易).
- 证明存在一个一一函数 将 映射到
利用反证法, 这两条事实结合起来可以推出 定理 2.1.
具体来说, 如果假设(为了反证)存在某个一一函数 将 映射到
那么通过将 与步骤 2 中的函数 复合得到的函数 就是从 到 的一一函数,
这与步骤 1 中的结论矛盾!
为了将这个想法完整地转化为 定理 2.1 的证明, 我们需要:
- 定义集合
- 证明不存在从 到 的一一函数.
- 证明存在从 到 的一一函数.
接下来我们将精确地做到这些:
我们将定义集合 它将扮演 的角色,
然后陈述并证明两个引理, 说明该集合满足我们所需的两个性质.
简单来说, 是一个 函数的集合, 并且一个函数 属于 当且仅当它的定义域是 而值域是
我们可以将 理解为所有无限长 比特序列 的集合, 因为函数 正好一一对应于无限序列
下面两个引理说明, 可以作为 来证明 定理 2.1:
引理 2.1. 不存在从 到 的一一映射 3
引理 2.2. 存在从 到 的一一映射 4
如上所示, 引理 2.1 和 引理 2.2 结合起来即可推出 定理 2.1.
为了更正式地重复这一论证, 为了反证, 假设存在一一函数
由 引理 2.2, 存在一一函数
因此, 根据假设, 由于两个一一函数的复合仍是一一函数(见 习题 2.12),
函数 定义为 将是一一函数,
这与 引理 2.1 矛盾.
参见 图 2.7 获取该论证的图示说明.
现在只剩下证明这两个引理. 我们先从证明 引理 2.1 开始, 这实际上是 定理 2.1 的核心部分.
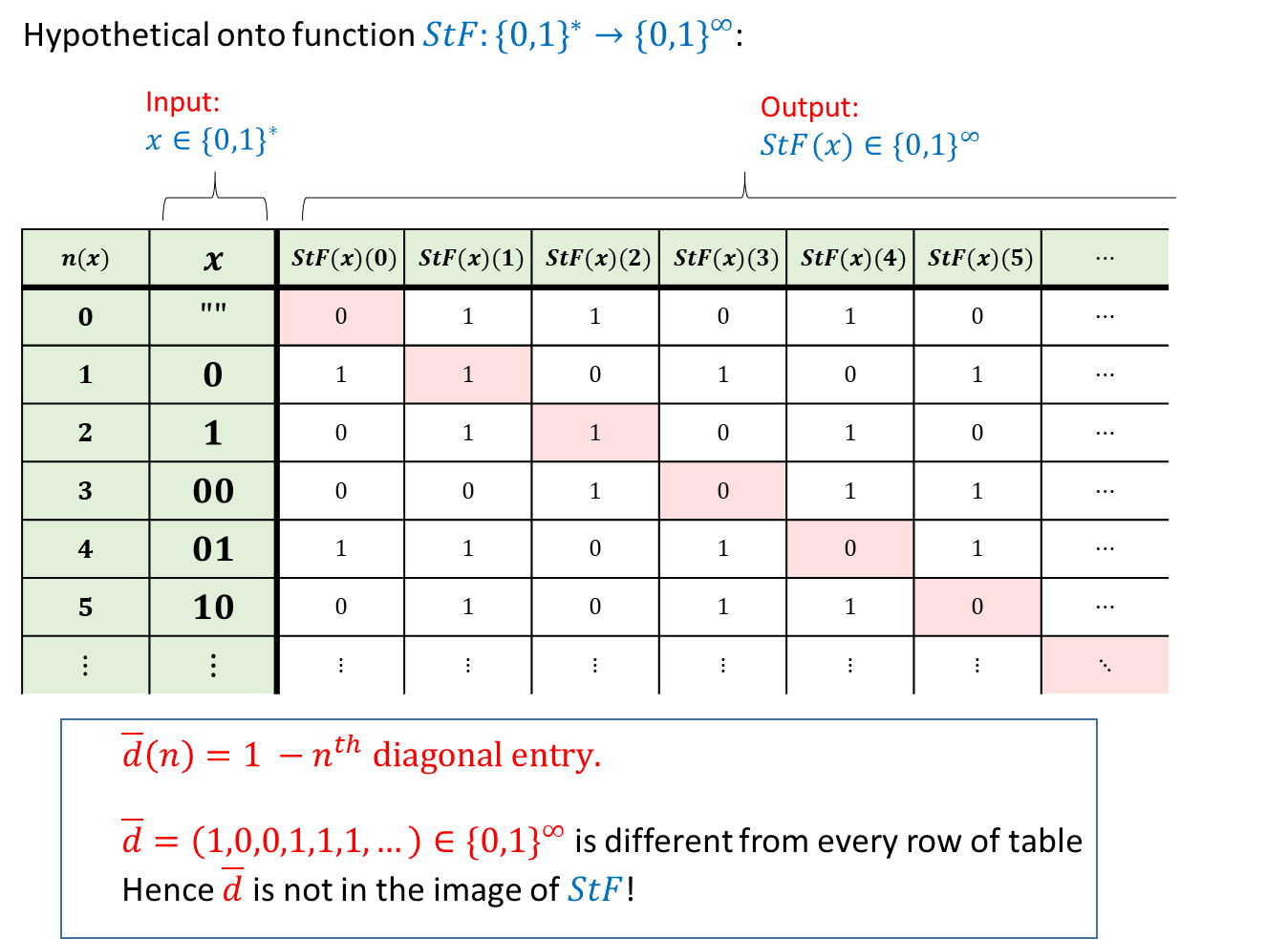
热身运动: “Cantor定理青春版”. 引理 2.1 的证明相当微妙. 一种获得对该证明的直觉的方法是考虑以下有限版本的陈述: “不存在一个满射函数 ”. 当然我们知道这是正确的, 因为集合 比集合 更大, 但让我们来看一个不太直接的证明: 对于任意 我们可以定义字符串 如下: 如果 是满射, 那么必然存在某个 使得 但我们声称不存在这样的 实际上, 如果存在这样的 那么 的第 个分量应当等于 但根据定义这个分量等于 另见此陈述的 “proof by code”.
对引理 2.1的证明
对引理 2.1的证明
我们将证明不存在一个 满射 函数
这将推出该引理, 因为对于任意两个集合 和 当且仅当存在一个从 到 的一一映射时, 才存在一个从 到 的满射 (见 引理 1.1).
这个证明技巧被称为 “diagonal argument” (对角线论证), 详情可见 图 2.8.
为了得到矛盾, 我们假设存在这样一个函数 然后我们通过构造一个函数 使得对每个 都有 来证明 不是满射.
考虑二进制字符串的字典序排列 (即 “”,
对于每个 我们令 为此顺序中的第 个字符串.
也就是说 等等.
对每个 我们定义函数 如下:
也就是说, 为了计算 在输入 时的值, 我们首先计算 其中 是字典序中的第 个字符串.
由于 它是一个将 映射到 的函数.
值 被定义为 的取反.
函数 的定义有些微妙.
一种理解方式是将函数 想象为由一张无限长的表格指定, 其中每一行对应一个字符串 (字符串按字典序排列), 并包含序列
然后, 我们取该表格中的 对角线 元素如下:
这些元素对应于表格中第 行第 列的 对于
我们上面定义的函数 将每个 映射到第 个对角线元素的取反值.
为了完成 不是满射的证明, 我们需要说明对每个 都有
事实上, 令 为某个字符串, 并令
如果 是 在字典序中的位置, 则根据构造有 这意味着 这正是我们需要的.
引理 2.1 实际上与自然数或字符串没有太大关系.
仔细审视这个证明可以发现, 它实际上说明对于 任意 集合 不存在一个一一映射 其中 表示所有以 为定义域的布尔函数的集合
由于我们可以将子集 与其特征函数 对应 (即 当且仅当 我们也可以将 看作 的所有 子集 的集合.
这个子集集合有时被称为 的 幂集, 记作 或
引理 2.1 的证明可以推广, 说明不存在一个集合与其幂集之间的一一映射.
特别地, 这意味着集合 “比” 更大.
Cantor 利用这些思想构建了无限的无穷层级.
这些无穷的数量远大于 甚至
他将 的基数记作 并将下一个更大的无限数记作 ( 是希伯来字母表的第一个字母).
Cantor 还提出了 连续统假设, 即
我们将在本书后续回到这个假设背后的精彩故事.
Aaronson 的这节讲座 提到了一些相关问题 (另见 Berkeley CS 70 lecture).
为了完成 定理 2.1 的证明, 我们需要证明 引理 2.2.
这个证明虽然需要一些微积分基础, 但使用了的地方都比较直接易懂.
不过如果你之前处理实数列极限的经验不多, 那么下面的证明还是可能会有些难以理解.
当然, 这部分并非 Cantor 论证的核心, 此类极限对于本书后续内容也不重要, 因此你完全可以选择相信 引理 2.2 并跳过这些繁琐的证明.
对引理 2.2的证明思路
对引理 2.2的证明思路
我们定义 为介于 和 之间的数, 其十进制展开为 换句话说,
如果 和 是 中的两个不同函数, 那么必然存在某个输入 使它们在该输入上不一致.
取最小的这样的 那么数字 与 在小数点后的第 到 位完全相同, 并在第 位上不同.
因此这些数字必然不同.
具体来说, 如果 且 则第一个数字大于第二个; 否则 ( 且 第一个数字小于第二个.
在证明中我们需要稍微注意, 因为某些数字可以被 无限展开, 例如, 数字 有两种十进制展开: 和
但在这里不会出现这个问题, 因为按上述定义, 我们使用的数字的十进制展开中永远不会包含数字
对引理 2.2的证明
对引理 2.2的证明
对于每个 我们定义 为其十进制展开为 的数字.
形式上,
在微积分中有一个已知结论(这里我们不重复证明): (2.2) 右侧的级数在 中收敛到一个确定的极限.
现在我们证明 是一一映射.
设 是 中的两个不同函数.
由于 和 不同, 必然存在某个输入它们的值不同, 我们令 为最小的这样的输入, 并且不失一般性地假设 且
(否则, 如果 且 我们可以简单地交换 和 的角色.)
数字 和 在小数点后的前 位完全相同.
由于这第 位在 中为 而在 中为 我们声称 比 至少大
要理解这一点, 注意 的差值在以下情况下最小: 对于所有 且 此时(由于 和 在前 位相同)
由于无穷级数 收敛到 可得对于每一对这样的 和
特别地, 我们看到对于每一对不同的 从而函数 是一一映射.
在上面的证明中, 我们使用了级数 收敛到 的事实, 将其代入 (2.3) 可得 与 的差值至少为
虽然我们为 选择的十进制表示是任意的, 但我们不能用二进制表示代替.
如果使用 二进制 展开而非十进制, 相应的级数 收敛到 并且由于 我们无法推导出 是一一映射.
事实上, 确实存在一些不同的序列对 满足
(例如, 序列 与序列 就具有此性质.)
2.4.1 推论: 布尔函数全体不可数.
Cantor 定理得出如下推论, 我们将在本书中多次使用: 所有 布尔函数(将 映射到 的函数)构成的集合是不可数的.
这是 引理 2.1 的直接推论, 因为我们可以用二进制表示构造一个从 到 的一一映射. 因此, 的不可数性意味着 的不可数性.
对定理 2.3的证明
对定理 2.3的证明
由于 是不可数的, 我们只需展示一个从 到 的一一映射, 便可得到该结论.
原因在于, 这样的映射存在意味着如果 是可数的, 从而存在一个从 到 的一一映射, 那么就会存在一个从 到 的一一映射, 与 引理 2.1 矛盾.
现在我们展示这个一一映射. 我们简单地将一个函数 映射到函数 如下.
我们令 等等.
也就是说, 对于每个 如果它在二进制下表示自然数 我们定义
如果 不表示这样的数字(例如, 它有前导零), 则我们令
这个映射是一一映射, 因为如果 是 中的两个不同元素, 那么必然存在某个输入 使
于是, 如果 是表示 的字符串, 我们看到 其中 是 映射到的 中的函数, 而 是 映射到的函数.
2.4.2 可数性的等价条件
上述结果建立了多种等价的方式来表述集合可数的事实.
具体来说, 以下陈述都是等价的:
- 集合 是可数的
- 存在一个从 到 的满射
- 存在一个从 到 的满射
- 存在一个从 到 的一一映射
- 存在一个从 到 的一一映射
- 存在一个从某个可数集合 到 的满射
- 存在一个从 到某个可数集合 的一一映射
2.5 数字以外元素的表示
当然, 数字并不是我们唯一可以表示为二进制字符串的对象.
用于表示某个集合 中对象的 表示方案 由一个将 中对象映射为字符串的 编码 函数和一个将字符串解码回 中对象的 解码 函数组成.
形式化地, 我们作如下定义:
注意, 对每个 都有 的条件意味着 是 满射(你能看出为什么吗? ).
事实上, 构造一个表示方案时, 我们只需要找到一个 编码 函数.
也就是说, 每个一一的编码函数都有对应的解码函数, 如下引理所示:
对引理 2.3的证明
对引理 2.3的证明
设 为 中任意一个元素.
对于每个 要么不存在, 要么仅存在一个 使 (否则 将不是一一映射).
我们将 定义为在第一种情况取 在第二种情况取该唯一对象
根据定义, 对每个 都有
虽然表示方案的解码函数通常可以是一个 局部 函数, 但 引理 2.3 的证明表明, 每个表示方案都有一个 全域 解码函数. 这一观察有时是很有用的.
2.5.1 有限表示
如果 是 有限 的, 那么我们可以将 中的每个对象表示为长度至多为某个数 的字符串.
那么 的取值是多少呢?
我们记 为长度至多为 的字符串集合
集合 的大小等于
这使用 等比数列 的标准求和公式即可得到.
为了将 中的对象表示为长度至多为 的字符串, 我们需要构造一个从 到 的一一映射. 而当且仅当 我们才能做到这一点, 如以下引理所示:
对于任意两个非空有限集合 当且仅当 时, 存在一个一一映射
设 且 并将 和 的元素分别写为 和
我们需要证明, 存在一个一一映射 当且仅当
对“当“方向, 如果 我们可以简单地定义 对每个
显然, 对于 有 因此该函数是一一映射.
对“仅当“方向, 假设 且 是某个函数. 那么 不可能是一一映射.
事实上, 对 我们“标记“ 中的元素
如果 已经被标记过, 那么我们就找到了两个映射到同一元素 的 中的对象.
否则, 由于 有 个元素, 当我们标记到 时, 中的所有对象都已被标记.
因此, 在这种情况下, 必须映射到一个已经被标记过的元素.
(这一观察有时被称为“鸽巢原理“: 假设有 个巢和 只鸽子, 则必有两只鸽子在同一个巢中.)
2.5.2 前缀无关编码
在展示有理数的表示方案时, 我们使用了一个“技巧“: 将字母表 编码, 以便将字符串元组表示为单个字符串.
这是 前缀无关编码 的一个特例.
前缀无关编码的思想如下, 如果我们的表示具有如下性质: 表示对象 的字符串 不是表示不同对象 的字符串 的 前缀 (即初始子串), 那么我们可以仅通过将列表中所有成员的表示串联起来, 来表示一个对象列表.
例如, 因为在英文中每个句子都以标点符号结束, 如句号, 感叹号或问号, 没有句子可以成为另一个句子的前缀, 因此我们可以仅通过将句子一个接一个地串联来表示一个句子列表. (英文中存在一些复杂情况, 例如缩写中的句点 (如 “e.g.”)或句子引号包含标点, 但高层次上前缀自由表示句子的原理仍然成立.)
事实上, 我们可以将 每一个 表示转换为前缀无关形式.
这为 重要提示 2.1 提供了依据, 并允许我们将类型 对象的表示方案转换为类型 对象 列表 的表示方案.
通过重复同样的技术, 我们还可以表示类型 对象的列表的列表, 以此类推.
但首先, 让我们正式定义前缀无关性:
回忆一下, 对于每个集合 集合 包含所有有限长度的元组(即 列表)的 中元素.
下述定理表明, 如果 是 的前缀自由编码, 则通过串联编码, 我们可以得到 的一个有效的(一一)表示:
定理 2.4 可能有点难以理解, 但一旦你理解了它的含义, 实际上证明起来相当直接.
因此, 我强烈建议你在此处停下来, 确保你理解了该定理的陈述. 你也应该尝试自己证明它, 然后再继续阅读.
证明的思路很简单.
例如, 假设我们想从表示 中解码三元组
我们首先找到 的第一个前缀 它是某个对象的表示.
然后解码该对象, 从 中去掉 得到新的字符串 再继续找到 的第一个前缀 以此类推(参见 习题 2.9).
的前缀自由性质保证了 实际上就是 是 依此类推.
对定理 2.4的证明
对定理 2.4的证明
现在我们给出正式证明.
使用反证法, 假设存在两个不同的元组 和 使得
我们将字符串 记为
设 为第一个使得 的索引.
(如果对所有 都有 由于假设这两个元组不同, 则其中一个元组的长度必须大于另一个. 在这种情况下, 不失一般性, 我们假设 并令 )
在 的情况下, 我们看到字符串 可以用两种不同的方式表示:
以及
其中 对所有 成立.
令 为从 中去掉前缀 后得到的字符串.
我们看到 可以写成两种形式: 对某个字符串 也可以写成 对某个
但这意味着 与 中的一个必须是另一个的前缀, 这与 的前缀自由性矛盾.
若 且 我们通过如下方式得到矛盾: 在这种情况下
这意味着 必须对应于空字符串
但在这种情况下, 也必须是空字符串, 而空字符串显然是任意其他字符串的前缀, 这与 的前缀自由性矛盾.
备注 2.6 (列表表示的前缀无关性).
即使集合 中对象的表示 是前缀无关的, 也并不意味着这些对象的 列表 的表示 也会是前缀无关的. 例如: 对于任意三个对象 列表 的表示将是列表 的表示的前缀.
然而, 如下的 引理 2.4 所示, 我们可以将 每一个 表示转换为前缀无关的, 因此如果需要表示列表的列表、列表的列表的列表等, 我们就可以使用该转换.
2.5.3 构造前缀无关表示
有一些自然的表示是前缀无关的.
例如, 每个 固定输出长度 的表示(即一一函数 自动是前缀无关的, 因为只有当 和 相等时, 长度相同的 才可能有 作为前缀.
此外, 我们用来表示有理数的方法也可以用来证明如下结论:
为了完整起见, 我们将在下方给出证明. 不过你可以在这里停下来, 尝试用我们表示有理数时使用的相同技巧自己证明它.
对引理 2.4证明
对引理 2.4证明
证明的核心思想是使用映射 来“加倍“字符串 中的每一位, 然后通过在其后拼接 来标记字符串的结束.
如果我们以这种方式对字符串 进行编码, 它可以确保 的编码绝不会是不同字符串 的编码的前缀.
形式上, 我们对每个 定义函数 如下:
如果 是 的(可能不是前缀无关的)表示, 我们可以通过定义 将其转换为前缀无关的表示
为了证明该引理, 我们需要证明 (1) 是一一函数, 并且 (2) 是前缀无关的.
事实上, 前缀无关是比一一更强的条件(如果两个字符串相等, 则其中一个必然是另一个的前缀), 因此只需证明 (2) 即可, 我们现在来证明它.
设 为 中两个不同的对象.
我们将证明 不是 的前缀, 或换句话说, 不是 的前缀, 其中
由于 是一一函数, 所以 我们分三种情况讨论, 取决于 或
- 如果 则 中位置 的两位为 而 中对应位将等于 或 (取决于 的第 位), 因此 不可能是 的前缀.
- 如果 由于 必然存在某个位置 使它们不同, 这意味着 和 在位置 上不同, 同样 不是 的前缀.
- 如果 则 因此 比 长, 不可能是其前缀.
在所有情况下, 我们可以预见 都不是 的前缀, 从而完成了证明.
引理 2.4 的证明并不是将任意表示转换为前缀无关形式的唯一方法, 也不一定是最优方法.
习题 2.10 就要求你构造一个更高效的前缀无关转换, 满足
2.5.4 “基于Python的证明” (选读)
定理 2.4 和 引理 2.4 的证明是 构造性的, 意味着它们给出了:
- 将任意对象 的表示的编码和解码函数转换为前缀无关的编码和解码函数的方法, 以及
- 将单个对象的前缀无关编码和解码扩展到 对象列表 的编码和解码的方法(通过串联实现).
具体来说, 我们可以将任意一对 Python 函数 encode 和 decode 转换为函数 pfencode 和 pfdecode, 对应于前缀无关的编码和解码.
同样, 给定单个对象的 pfencode 和 pfdecode, 我们可以将它们扩展到列表的编码.
下面展示了如何对上文定义的 NtS 和 StN 函数进行这种处理.
我们从 引理 2.4 的“Python 证明“开始: 一种将任意表示转换为 前缀无关 表示的方法.
下面的函数 prefixfree 接受一对编码和解码函数作为输入, 并返回一个三元组函数, 其中包含 前缀无关 的编码和解码函数, 以及一个检查字符串是否为对象有效编码的函数.
# 接受 encode 和 decode 函数, 分别将对象映射为比特列表以及反向映射,
# 并返回 pfencode 和 pfdecode 函数,
# 以前缀无关的方式将对象映射为比特列表以及反向映射.
# 同时返回一个 pfvalid 函数, 用于判断一个比特列表是否为有效编码
def prefixfree(encode, decode):
def pfencode(o):
L = encode(o)
return [L[i//2] for i in range(2*len(L))]+[0,1]
def pfdecode(L):
return decode([L[j] for j in range(0,len(L)-2,2)])
def pfvalid(L):
return (len(L) % 2 == 0 ) and all(L[2*i]==L[2*i+1] for i in range((len(L)-2)//2)) and L[-2:]==[0,1]
return pfencode, pfdecode, pfvalid
pfNtS, pfStN , pfvalidN = prefixfree(NtS,StN)
NtS(234)
# 11101010
pfNtS(234)
# 111111001100110001
pfStN(pfNtS(234))
# 234
pfvalidM(pfNtS(234))
# true
注意, 上述 Python 函数 prefixfree 接受两个 Python 函数 作为输入, 并输出三个 Python 函数作为结果. (无歧义的情况下, 我们会使用 “Python 函数” 或 “子程序” 这个术语来区分 Python 程序片段和数学意义上的函数.)
在本书中, 你不需要掌握 Python, 但你需要熟悉函数作为独立的数学对象的概念, 可以被用作其他函数的输入或输出.
下面我们给出 定理 2.4 的 “Python 证明”. 具体来说, 我们展示一个函数 represlists, 它接受一个前缀无关表示方案作为输入 (通过编码、解码和有效性检测函数实现), 并输出一个用于表示该类对象 列表 的表示方案. 如果我们希望使这个表示也是前缀无关的, 那么可以再将其放入上面的 prefixfree 函数中.
def represlists(pfencode,pfdecode,pfvalid):
"""
接受函数 pfencode, pfdecode 和 pfvalid,
并返回函数 encodelists, decodelists,
它们可以分别对该类对象的 **列表** 进行编码和解码.
"""
def encodelist(L):
"""Gets list of objects, encodes it as list of bits"""
return "".join([pfencode(obj) for obj in L])
def decodelist(S):
"""Gets lists of bits, returns lists of objects"""
i=0; j=1 ; res = []
while j<=len(S):
if pfvalid(S[i:j]):
res += [pfdecode(S[i:j])]
i=j
j+= 1
return res
return encodelist,decodelist
LtS , StL = represlists(pfNtS,pfStN,pfvalidN)
LtS([234,12,5])
# 111111001100110001111100000111001101
StL(LtS([234,12,5]))
# [234, 12, 5]
2.5.5 字母和文本的表示
我们可以用一个字符串来表示一个字母或符号, 然后如果这种表示是前缀无关的, 我们就可以通过简单地连接每个符号的表示来表示一个符号序列.
其中一种表示是 ASCII, 它用 7 位的字符串表示 128 个字母和符号.
由于 ASCII 表示是固定长度的, 它自动是前缀无关的 (你能看出原因吗?).
Unicode 是一种将 (在撰写本文时) 约 128,000 个符号表示为介于 0 和 1,114,111 之间的数字的表示方法 (称为 code points).
对于这些 code points 有几种前缀无关的表示方法, 一种流行的方法是 UTF-8, 它将每个 code point 编码为长度在 8 到 32 之间的字符串.
样例 2.2 (Braille 编码(盲文)).
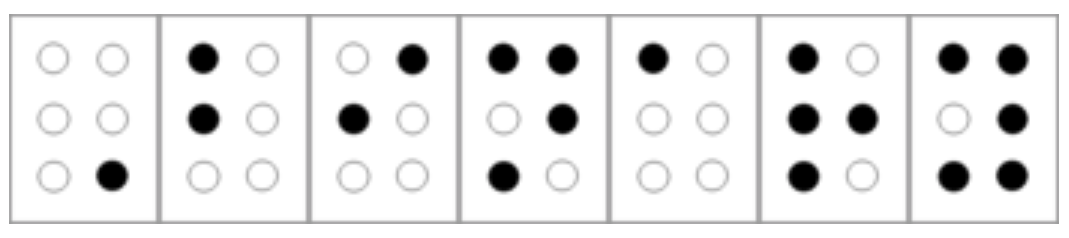
Braille 编码(盲文) 是另一种将字母和其他符号编码为二进制字符串的方法. 具体来说, 在盲文中, 每个字母被编码为一个属于 的字符串, 该字符串通过排列成两列三行的凸起点来书写, 参见 图 2.10.
(一些符号需要用超过一个六位字符串来编码, 因此盲文使用了更通用的前缀无关编码.)
Louis Braille 是一个法国男孩, 因事故在 5 岁时失明. 盲文由 Braille 于 1821 年发明, 当时他只有 12 岁 (尽管他在一生中不断改进和完善它).
样例 2.3 (C语言中对象的表示(选读)).
我们可以使用编程语言来探究我们的计算环境如何表示各种数值.
在允许直接访问内存的 “不安全” 编程语言(如 C语言)中, 这种操作最为简单.
使用一个 简单的 C 程序, 我们可以得到各种数值的表示方法.
可以看到, 对于整数, 乘以 2 对应于每个字节内部的 “左移”.
相比之下, 对于浮点数, 乘以 2 对应于表示中指数部分加 1.
在我们使用的架构中, 负数使用 二进制补码 方法表示.
C语言通过确保字符串末尾有一个零字节, 来以前缀无关的形式表示字符串.
int 2 : 00000010 00000000 00000000 00000000
int 4 : 00000100 00000000 00000000 00000000
int 513 : 00000001 00000010 00000000 00000000
long 513 : 00000001 00000010 00000000 00000000 00000000 00000000 00000000 00000000
int -1 : 11111111 11111111 11111111 11111111
int -2 : 11111110 11111111 11111111 11111111
string Hello: 01001000 01100101 01101100 01101100 01101111 00000000
string abcd : 01100001 01100010 01100011 01100100 00000000
float 33.0 : 00000000 00000000 00000100 01000010
float 66.0 : 00000000 00000000 10000100 01000010
float 132.0: 00000000 00000000 00000100 01000011
double 132.0: 00000000 00000000 00000000 00000000 00000000 10000000 01100000 01000000
2.5.6 向量, 矩阵及图片的表示
一旦我们可以表示数字和数字列表, 我们就可以表示 向量(本质上就是数字的列表).
同样, 我们可以表示列表的列表, 因此特别地, 可以表示 矩阵.
为了表示一张图像, 我们可以通过一个长度为3的数字列表表示每个像素的颜色, 分别对应红色、绿色和蓝色的强度.
(我们可以只使用三种原色, 因为 大多数 人类视网膜中只有三种类型的视锥细胞; 而如果要表示 螳螂虾 可见的颜色, 我们需要 16 种原色.)
因此, 一张包含 个像素的图像可以表示为一个包含 个长度为三的列表的列表.
视频可以表示为图像的列表.
当然, 这些表示方法相当浪费, 对于图像和视频通常使用 更 紧凑 的表示方法, 虽然本书不会涉及这些内容.
2.5.7 图的表示
一个 图 在 个顶点上可以表示为一个 的 邻接矩阵, 其第 个元素为 1 当且仅当边 存在, 否则为 0.
也就是说, 我们可以将一个 顶点的有向图 表示为一个字符串 使得 当且仅当边
我们可以通过将每条无向边 替换为两条有向边 和 来将无向图转换为有向图.
另一种图的表示方法是 邻接表 表示. 也就是说, 我们将图的顶点集合 与集合 对应, 其中 并将图 表示为 个列表组成的列表, 其中第 个列表包含顶点 的出邻居.
对于某些应用, 这些表示方法之间的差异可能很大, 虽然对于我们而言通常无关紧要.
2.5.8 列表和嵌套列表的表示
如果我们有一种方法将集合 中的对象表示为二进制字符串, 那么我们可以通过应用前缀无关变换来表示这些对象的列表.
此外, 我们可以使用类似上述的技巧来处理 嵌套 列表.
其思想是, 如果我们有某种表示 那么我们可以使用五元素字母表 0,1,[ , ] , , 上的字符串来表示来自 的嵌套列表.
例如, 如果 表示为 0011, 表示为 10011, 表示为 00111, 那么我们可以将嵌套列表 表示为字母表 上的字符串 "[0011,[10011,00111]]".
通过将 的每个元素本身编码为三位二进制字符串,
我们可以将任意对象集合 的表示转换为一种表示, 使得可以表示这些对象的(潜在嵌套)列表.
2.5.9 一些注释
我们通常会将一个对象与其字符串表示等同起来.
例如, 如果 是某个将字符串映射到字符串的函数, 且 是一个整数, 我们可能会说 “ 是质数”, 这意味着如果我们将 表示为字符串 那么由字符串 表示的整数 满足 是质数.
(你可以看到, 这种将对象与其表示等同的约定可以为我们节省大量繁琐的形式化表达.)
同样地, 如果 是某些对象, 且 是一个以字符串为输入的函数, 那么 表示将 应用于有序对 的表示的结果.
我们对任意 元组对象使用相同的符号表示函数的调用.
这种将对象与其字符串表示等同的约定, 是我们人类一直在使用的.
例如, 当人们说 “ 是质数” 时, 他们真正的意思是, 十进制表示为字符串 “17” 的整数是质数.
当我们说
“ 是一个计算自然数乘法的算法”
时, 我们真正的意思是
“ 是一个计算函数 的算法, 满足对于每一对 如果 是表示有序对 的字符串, 那么 将是表示它们乘积 的字符串”.
天呐!
2.6 将计算任务定义为数学函数
抽象地讲, 计算过程 是一种将输入(二进制字符串)转换为输出(二进制字符串)的过程.
这种从输入到输出的变换可以通过现代计算机、遵循指令的人、某些自然系统的演化或其他任何手段完成.
在后续章节中, 我们将转向对计算过程的数学定义, 但正如上文所讨论的, 目前我们关注 计算任务. 也就是说, 我们关注的是 规范 而非 实现.
同样地, 在抽象层面上, 一个计算任务可以指定输出需要满足的任意输入输出关系.
然而, 在本书的大部分内容中, 我们将专注于最简单、最常见的任务: 计算函数.
下面是一些例子:
- 给定两个整数 的表示, 计算它们的乘积 使用上面的表示方法, 这对应于从 到 的函数计算. 我们已经看到, 解决这个计算任务的方法不止一种, 事实上, 我们仍然不知道该问题的最优算法.
- 给定一个整数 的表示, 计算其 因式分解; 即, 找出质数列表 使得 这同样对应于从 到 的函数计算. 对于该问题的复杂性, 我们的认知差距甚至更大.
- 给定图 的表示和两个顶点 与 计算 中从 到 的最短路径长度, 或者计算从 到 的 最长路径(不重复顶点)的长度. 这两个任务都对应于从 到 的函数计算, 但它们的计算难度却差别极大.
- 给定一个 Python 程序的代码, 判断是否存在输入会使程序进入无限循环. 该任务对应于从 到 的 部分函数 计算, 因为并非每个字符串都对应语法有效的 Python 程序. 我们会看到, 我们 确实 理解该问题的计算状态(见下文的状态机), 但答案相当令人惊讶.
- 给定图像 的表示, 判断 是猫的照片还是狗的照片. 这对应于从 到 的某个(部分)函数的计算.
计算任务的一个重要特例是计算 布尔函数, 其输出为单比特
计算这类函数对应于回答 是/否 问题, 因此该任务也被称为 判定问题.
给定任意函数 和 计算 的任务对应于判定 是否属于集合 其中 被称为与函数 对应的 语言.(语言这个术语源于计算理论与诺姆·乔姆斯基发展的形式语言学之间的历史联系.)
因此, 许多文献将这类计算任务称为 判定一个语言.
对于每一个特定函数 可能存在多种 算法 来计算
我们将关注如下问题:
- 对于给定函数 是否可能 不存在算法 来计算 ?
- 如果存在算法, 哪一个是最优的? 是否可能 在某种意义上是 “有效不可计算“的, 即计算 的每个算法都需要极其庞大的资源?
- 如果我们无法回答这个问题, 能否在不同函数 和 之间证明某种等价性, 即它们要么都容易(有快速算法), 要么都困难?
- 一个函数难以计算是否可能是 好事? 我们能否将其应用于密码学等领域?
为了回答这些问题, 我们需要对 算法 的概念进行数学定义, 这将在 第三章 中完成.
2.6.1 注意区分 函数 和 程序!
你应始终注意 规范 与 实现 之间可能产生的混淆, 或等价地, 数学函数 与 算法/程序 之间的混淆.
编程语言(包括 Python)使用 函数 这个术语来表示(部分)程序, 这只会增加混乱.
这种混淆还源于数千年的数学历史, 在历史上人们通常通过一种计算方法来定义函数.
例如, 考虑自然数上的乘法函数.
这是函数 将一对自然数 映射为它们的乘积
正如我们提到的, 它可以通过多种方式实现:
def mult1(x,y):
res = 0
while y>0:
res += x
y -= 1
return res
def mult2(x,y):
a = str(x) # represent x as string in decimal notation
b = str(y) # represent y as string in decimal notation
res = 0
for i in range(len(a)):
for j in range(len(b)):
res += int(a[len(a)-i])*int(b[len(b)-j])*(10**(i+j))
return res
print(mult1(12,7))
# 84
print(mult2(12,7))
# 84
无论是 mult1 还是 mult2, 给定相同的自然数输入对, 都会产生相同的输出.
(不过当数字变大时, mult1 所需时间会长得多.)
因此, 尽管它们是两个不同的 程序, 它们计算的是相同的 数学函数.
区分 程序或算法 与 计算的函数 对本课程至关重要 (参见 图 2.13).
区分 函数 与 程序(或其他计算方式, 包括 电路 和 机器)是本课程的一个核心主题.
因此, 这也是我(以及许多其他教师)在作业和考试中经常提出的问题主题(暗示一下, 暗示一下).
备注 2.7 (超越于函数的计算 (进阶主题, 选读)).
函数能够涵盖相当多的计算任务, 但我们也可以考虑更一般的情形.
首先, 我们可以且将要讨论 部分函数, 它们并不在所有输入上都有定义.
在计算部分函数时, 我们只需关注函数定义域内的输入.
换句话说, 我们可以在假设有人“承诺“所有输入 都使得 有定义的前提下, 设计部分函数 的算法(否则我们不关心结果).
因此, 这种任务也被称为 承诺问题 (promise problems).
另一种推广是考虑 关系, 它可能有多个可接受的输出.
例如, 考虑求解给定方程组的任意解的任务.
一个 关系 将字符串 映射为一个 字符串集合 (例如, 可能描述一组方程, 此时 对应于 的所有解的集合).
我们也可以将关系 与字符串对 的集合对应起来, 其中
如果一个计算过程对于每个 都输出某个 则称它求解了关系
在本书后续章节, 我们将考虑更一般的任务, 包括 交互式任务(如在游戏中寻找良好策略)、使用概率概念定义的任务等.
然而, 在本书的大部分内容中, 我们将专注于 计算函数 的任务, 并且常常是 布尔函数, 输出仅为单比特.
事实证明, 在这个任务背景下可以研究大量计算理论, 所获得的见解在更一般的情形中同样适用.
- 我们可以使用二进制字符串来表示希望计算的对象.
- 一个集合 的表示方案是从 到 的一一映射.
- 我们可以使用前缀无关编码将集合 的表示“升级“为集合中元素列表的表示.
- 一个基本的计算任务是 计算函数 的任务. 这个任务不仅包括乘法、因式分解等算术计算, 还涵盖了科学计算、人工智能、图像处理、数据挖掘等众多领域中的其他任务.
- 我们将研究如何找到(或至少给出界限)计算各种有趣函数 的 最优算法 的问题.
2.7 习题
习题 2.1.
以下哪个对象可以用二进制字符串表示?
a. 一个整数
b. 一个无向图
c. 一个有向图
d. 以上所有
习题 2.2 (二进制表示). a. 证明在 (2.1) 中定义的二进制表示函数 满足对于每个 如果 那么 且
b. 给出一个函数 使得对于每个 都有 从而证明 是一个单射函数.
习题 2.3 (更加紧凑的ASCII表示). ASCII 编码可以将由 个英文字母组成的字符串编码为一个 位的二进制字符串, 但在本练习中, 我们要求为小写英文字母字符串寻找一种更紧凑的表示方法.
-
证明存在一种表示方案 用于将字母表 (共 26 个字母)上的字符串编码为二进制字符串, 使得对于每个 和长度为 的字符串 表示 是一个长度不超过 的二进制字符串. 换言之, 证明对于每个 存在一个单射函数
-
证明不存在一种表示方案, 用于将字母表 上的字符串编码为二进制字符串, 使得对于每个长度为 的字符串 表示 是一个长度为 的二进制字符串. 换言之, 证明存在某个 使得不存在单射函数
-
Python 的
bz2.compress函数是一个从字符串到字符串的映射, 它使用无损(因此是单射)的 bzip2 算法进行压缩. 在转换为小写并截去空格和数字后, 托尔斯泰的《战争与和平》文本包含 个字符. 然而, 如果我们对《战争与和平》的文本字符串运行bz2.compress, 会得到一个长度为 位的字符串, 这只有 (尤其远小于 解释为什么这不与你对前一个问题的回答相矛盾. -
有趣的是, 如果我们尝试对随机字符串应用
bz2.compress, 性能会差得多. 在我的实验中, 输出位数与输入字符数之间的比率约为 然而, 有人可能会想象可以做得更好, 并且存在一家名为“Pied Piper”的公司, 其算法可以将由 个随机小写字母组成的字符串无损压缩到少于 位. 5 通过证明对于每个 和单射函数 如果我们令 为随机变量 (即 的长度), 其中 是从集合 中均匀随机选择的, 则 的期望值至少为 来说明这种情况不可能发生.
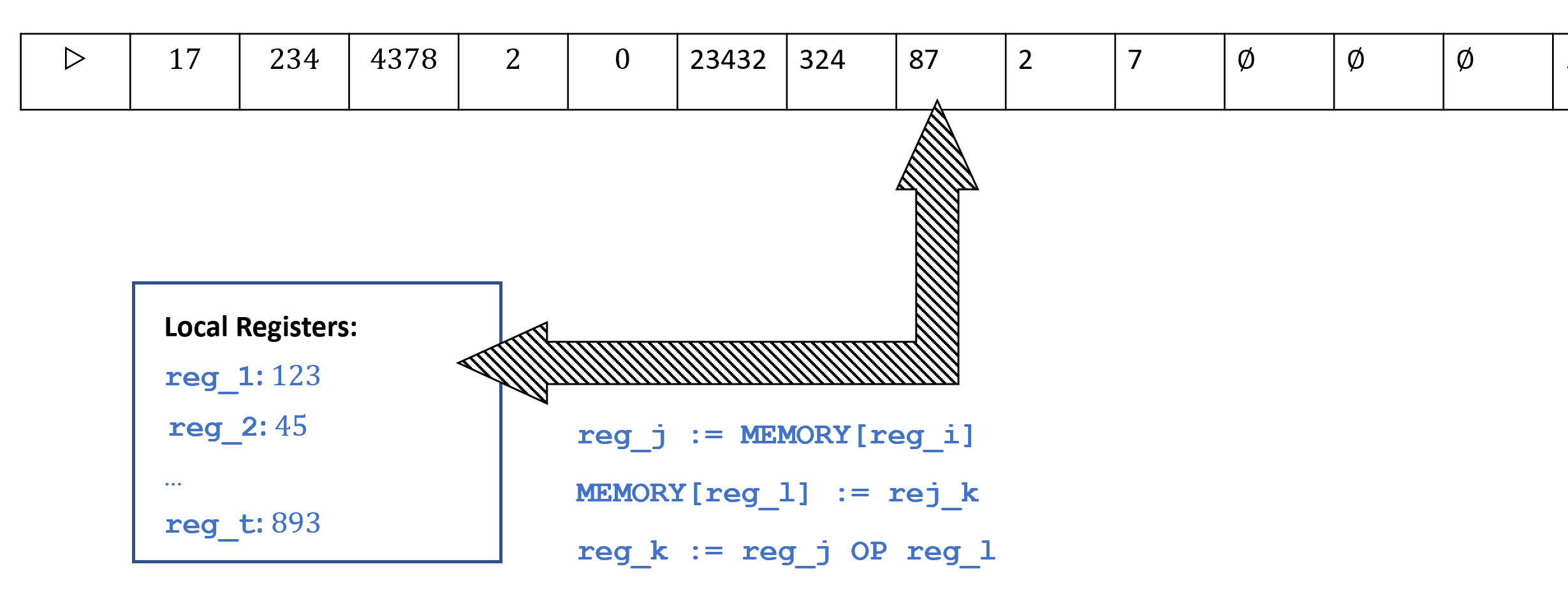
习题 2.7. 假设 对应于将一个数 表示为一个由 个 1 组成的字符串( 例如, 等). 如果 和 是介于 和 之间的数, 那么当以 表示形式给出它们时, 我们是否仍然能用 次操作将 和 相乘?
习题 2.8. 回忆一下, 如果 是一个一一对应且满射的函数, 将有限集 中的元素映射到有限集 那么 和 的大小相同. 令 是一个函数, 使得对于每个 是 的二进制表示.
证明 当且仅当
使用第1题来计算集合 的大小, 其中 表示字符串 的长度.
使用第1题和第2题来证明
习题 2.10 (更高效的前缀无关转换). 假设 是集合 中对象的一种表示法( 不一定前缀无关), 且 是自然数的一种前缀无关表示法. 定义 ( 即, 将 的长度的表示与 本身连接起来).
a. 证明 是 的一种前缀无关表示法.
b. 证明我们可以通过一种修改将任何表示法转换为前缀无关的表示法, 该修改将一个 位字符串转换为长度至多为 的字符串.
c. 证明我们可以通过一种修改将任何表示法转换为前缀无关的表示法, 该修改将一个 位字符串转换为长度至多为 的字符串. 6
- 我们已经证明了自然数可以表示为字符串. 证明反方向也成立: 存在一个一对一映射 ( 表示“字符串到数字”. )
- 回忆一下, Cantor 证明了不存在一对一映射 证明 Cantor 的结果蕴含 定理 2.1.
2.8 参考书目
将数据表示为字符串的研究( 包括 压缩 和 纠错 等问题)属于 信息论 的范畴, 这在 Cover 和 Thomas 的经典教材 (Cover, Thomas, 2006) 中有涵盖. 表示法也在 数据结构设计 领域中被研究, 相关教材如 (Cormen, Leiserson, Rivest, Stein, 2009).
关于用最高有效位在前还是在后表示整数的问题, 被称为大端序与小端序表示法. 这一术语来源于 Cohen 的 (Cohen, 1981) 那篇兼具趣味性与知识性的论文, 他在文中将两派拥护者之间的冲突比作乔纳森·斯威夫特的《格列佛游记》中交战不休的部落. 有符号整数的二进制补码表示法是在冯·诺依曼的经典报告 (von Neumann, 1945) 中提出的, 该报告详细阐述了存储程序计算机的设计方案, 不过类似的表示法甚至更早就在算盘和其他机械计算设备中得到了使用.
我们应当将函数的 定义 或 规范 与其 实现 或 计算 分离开来, 这一想法看似“显而易见“, 但数学家们花了相当长的时间才达成这一观点. 历史上, 函数 是通过展示如何从输入推导出输出的规则或公式来标识的. 正如我们在第9章中更深入讨论的那样, 在 19 世纪, 这种有些非正式的函数概念开始“出现裂痕“, 最终数学家们得出了更严谨的定义, 即函数是输入到输出的任意赋值. 虽然许多函数可以通过一个或多个公式来描述( 或计算), 但如今我们并不认为这是函数的基本属性, 也允许存在不对应于任何“优美“公式的函数.
我们已经提到, 实数的所有表示法本质上都是 近似的. 因此, 一项重要的努力是理解, 我们能够就算法输出的近似质量提供何种保证, 并将其作为输入近似质量的函数. 这个问题被称为确定给定方程的数值稳定性的问题. 浮点数指南网站 详细描述了浮点数表示法及其可能微妙失效的多种方式, 另请参阅网站 0.30000000000000004.com.
Dauben (Dauben, 1990) 撰写了康托尔的传记, 重点介绍了他的数学思想发展历程. (Halmos, 1960) 是一本关于集合论的经典教材, 也包括了康托尔定理. 康托尔定理也在许多离散数学教材中有所涵盖, 包括 (Meyer, 2018)(Lewis, Zax, 2019).
图的邻接矩阵表示法不仅仅是将图映射成二进制字符串的便捷方法, 而且事实证明, 矩阵的许多自然概念和运算对图也很有用. ( 例如, 谷歌的 PageRank 算法就依赖于这一观点. )Spielman 课程 的笔记是这个领域( 称为 谱图论 )的极佳资源. 我们将在本书后面讨论 随机游走 时, 重新回到这一观点.
1: 尽管巴比伦人早已发明了位置记数法, 我们今天使用的十进制位置记数法是印度数学家约在公元三世纪发明的, 再由阿拉伯数学家在八世纪采用与发展. 它在欧洲首次受到显著关注是在 1202 年 Fibonacci(又名 Leonardo of Pisa)出版的著作 “Liber Abaci” 中, 但直到十五世纪, 它才在日常使用中取代罗马数字.
2: 其中 代表 “real numbers to strings”.
3: 代表 “functions to strings”.
4: 代表 “functions to reals”.
5: 实际上, 这家虚构公司使用的指标更关注压缩速度而非压缩率, 参见这里和这里.
6: 提示: 递归地思考如何表示字符串的长度.
- 定义计算
定义计算
“没有理由不借助机器来节省脑力劳动和体力劳动. “ – Charles Babbage, 1852
“如果有谁不以我的例子为戒, 而尝试并成功地用不同的原理或更简单的机械手段, 构造出一台在自身中体现数学分析执行部门全部功能的机器, 那么我丝毫不担心将我的声誉交付于他, 因为唯有他能完全理解我努力的性质及其成果的价值. “ – Charles Babbage, 1864
“要理解一个程序, 你必须既成为机器, 又成为程序. “ – Alan Perlis, 1982
学习目标
- 理解计算可以被精确建模.
- 学习 布尔电路 / 直线程序 的计算模型.
- 电路与直线程序的等价性.
- // 与 的等价性.
- 物理世界中的计算实例.

图 3.2. 摘自 Popular Mechanics 上的一篇关于 Harvard Mark I 计算机的文章, 1944 年.
几千年来, 人类一直在进行计算, 不仅依靠纸笔, 还使用过算盘、计算尺、各种机械装置, 直到现代的电子计算机. 从先验的角度来看, 计算这一概念似乎总是依赖于所使用的具体工具. 例如, 你也许会认为, 在现代笔记本电脑上用 Python 实现的乘法算法, 与用纸笔进行乘法运算时的“最佳“算法会有所不同.
然而, 正如我们在引言中所看到的, 一个在渐近意义上更优的算法, 无论底层技术如何, 最终都会优于较差的算法. 这让我们看到希望: 可以找到一种独立于技术的方式来刻画计算的概念.
本章正是要做这件事. 我们将把“从输入计算输出“定义为一系列基本操作的应用 (见图 3.3) . 借助这一框架, 我们便能精确地表述诸如: “函数 可以由模型 计算“或“函数 可以由模型 在 步操作内计算完成“这样的命题.
阅读本章, 我们希望读者能够有以下收获:
-
我们可以使用 逻辑运算, 如 (与)、(或) 和 (非), 从输入计算输出 (见 3.2节) .
-
布尔电路 是一种通过组合基本逻辑运算来计算更复杂函数的方法 (见 3.3节) .
我们既可以将布尔电路看作一种数学模型 (基于有向无环图) , 也可以将其视为现实世界中可实现的物理装置. 实现方式多种多样, 不仅包括基于硅的半导体, 还包括机械甚至生物机制 (见 3.5节) . -
我们还可以把布尔电路描述为 直线型程序, 即不包含循环结构的程序 (没有
while/for/do .. until等) (见 3.4节) . -
可以通过 运算来实现 、 和 运算 (反之亦然) .
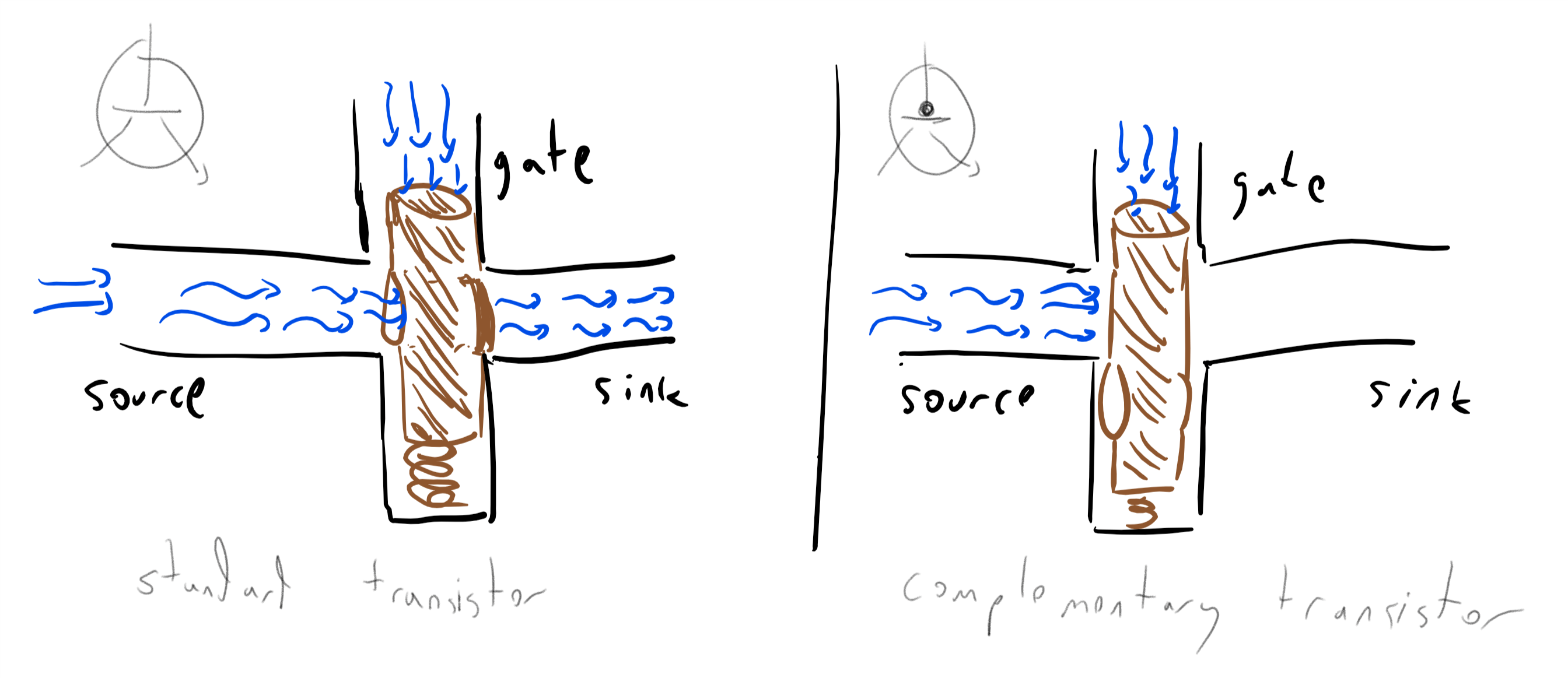
这意味着带有 // 门的电路, 与带有 门的电路在计算能力上是等价的, 我们可以根据需要选择其中任一模型来描述计算 (见 3.6节) .
先提前剧透一下, 在 下一章 中我们将看到, 这类电路可以计算所有有限函数.
本章的一个“重要启示“是 模型之间的等价性 (见重要提示 3.1) . 如果两个计算模型能够计算相同集合的函数, 那么它们就是等价的. 布尔电路 (// 门) 与 电路的等价性只是一个例子, 本书中我们还会多次遇到类似的普遍现象.
3.1 定义计算
“算法“一词来源于对穆罕默德·伊本·穆萨·花剌子密(Muhammad ibn Musa al-Khwarizmi)名字的拉丁化转写. al-Khwarizmi 是九世纪的一位波斯学者, 他的著作向西方世界介绍了十进位值制数字系统, 以及一次方程与二次方程的解法 (见 图 3.4) . 然而, 以今天的标准来看, al-Khwarizmi 对算法的描述的形式化程度相当不足. 他没有使用如 这样的变量, 而是采用具体的数字 (如 10 和 39) , 并依赖读者从这些例子中自行类推出一般情况–这与当今儿童学习算法时的教学方式颇为相似.
以下是 al-Khwarizmi 对解形如 方程的算法的描述:
举例来说: “一个平方加上它的十倍平方根等于三十九迪拉姆. “ 换句话说, 求这样一个平方数: 它加上它自身的十倍平方根, 结果是三十九.
解法如下:
- 将根的数量减半, 本例中十的一半是五.
- 将这个数 (五) 平方, 得到二十五.
- 将平方结果加到三十九上, 得到六十四.
- 取六十四的平方根, 得到八.
- 从平方根中减去根数量的一半 (五) , 余数为三.
因此, 这个平方根为三, 对应的平方为九.
为了本书的目的, 我们需要一种更加精确的方式来描述算法. 幸运 (或者说不幸) 的是, 至少目前, 计算机在从实例中学习方面远远落后于学龄儿童. 因此, 在 20 世纪, 人们提出了用于精确描述算法的形式化语言, 即 编程语言.
下面是用 Python 转写的 al-Khwarizmi 二次方程求解算法:
from math import sqrt
# 使用 Python 的 sqrt 函数来计算平方根
def solve_eq(b, c):
# 根据 al-Khwarizmi 的方法求解 x^2 + b*x = c
# al-Khwarizmi 在 b=10, c=39 的例子中演示了这个方法
val1 = b / 2.0 # "将根的数量减半"
val2 = val1 * val1 # "将这个数平方"
val3 = val2 + c # "将平方结果加到 c 上"
val4 = sqrt(val3) # "取和的平方根"
val5 = val4 - val1 # "从平方根中减去根数量的一半"
return val5 # "这就是所求的平方根"
# 测试: 求解 x^2 + 10*x = 39
print(solve_eq(10, 39))
# 输出 3.0
我们可以非正式地定义算法如下:
在本章中, 我们将使用 布尔电路 (Boolean Circuits) 模型, 更精确而正式地定义算法. 我们将展示, 布尔电路在计算能力上等价于用“极简“编程语言编写的 直线程序 (straight line programs), 即不包含循环的编程语言. 我们还将看到, 具体选择哪种 基本运算 (elementary operations) 并不重要, 不同的选择都可以得到计算能力等价的模型 (见图 3.6). 然而, 要理解这一点, 我们需要一些时间. 我们将从讨论什么是“基本运算“开始, 并说明如何将算法的描述映射为实际物理过程, 使其在现实世界中从输入生成输出.
3.2 使用与( 或( 非(进行计算
算法的表示需要将一个较为复杂的计算分解为一系列更简单的步骤. 这些步骤可以通过多种不同的方式来执行, 包括:
- 在纸上书写符号.
- 改变电线中的电流.
- 蛋白质与 DNA 链结合.
- 集体中的个体对刺激做出反应 (例如, 蜂群中的蜜蜂, 市场中的交易者) .
为了形式化地定义算法, 我们尝试“化繁为简“, 挑出组成算法的“最小单位“, 例如下列一组简单逻辑函数:
- 与函数 定义为
- 或函数 定义为
- 非函数 定义为
函数 、 和 是逻辑学以及许多计算机系统中使用的基本逻辑运算符. 在逻辑学中, 表示为 表示为 表示为 或 我们也将采用这种表示法.
每一个函数 都以一个或两个单比特作为输入, 并输出一个单比特. 尽管这些运算看起来相当基本, 然而, 计算的威力正来源于将这些简单的运算组合在一起.
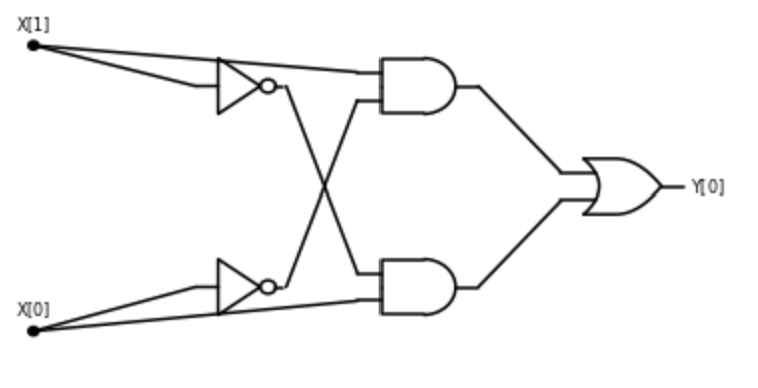
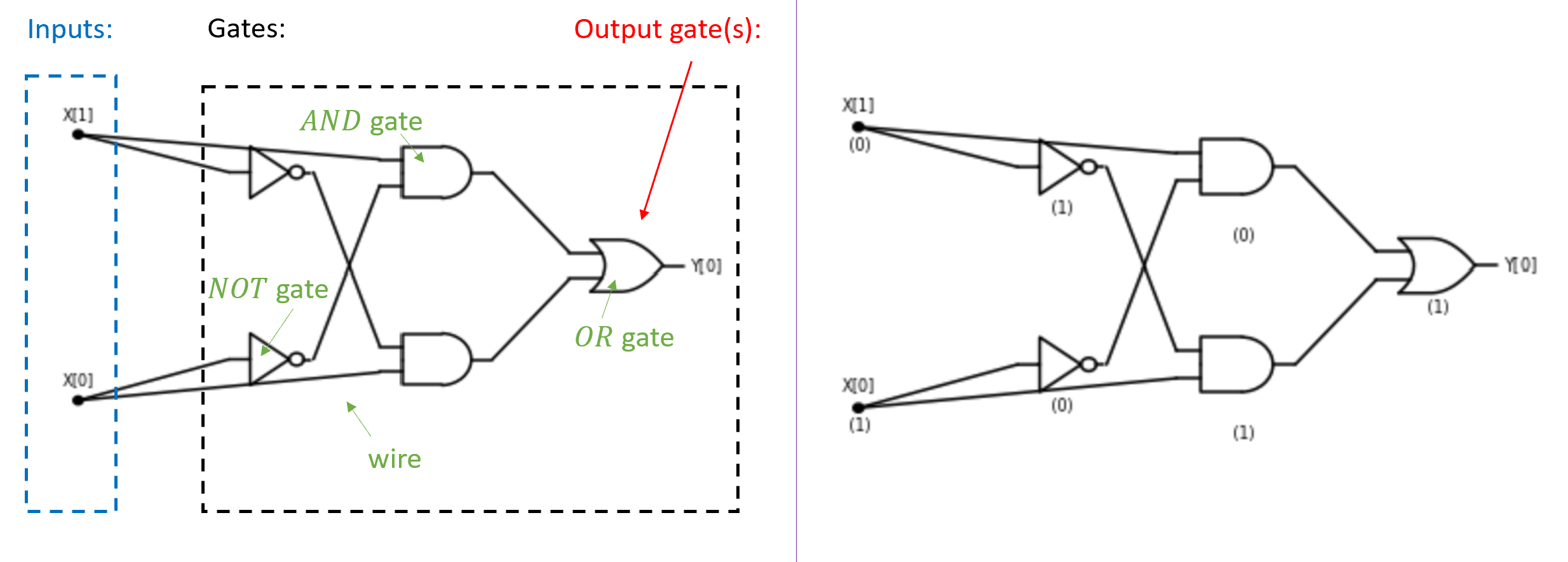
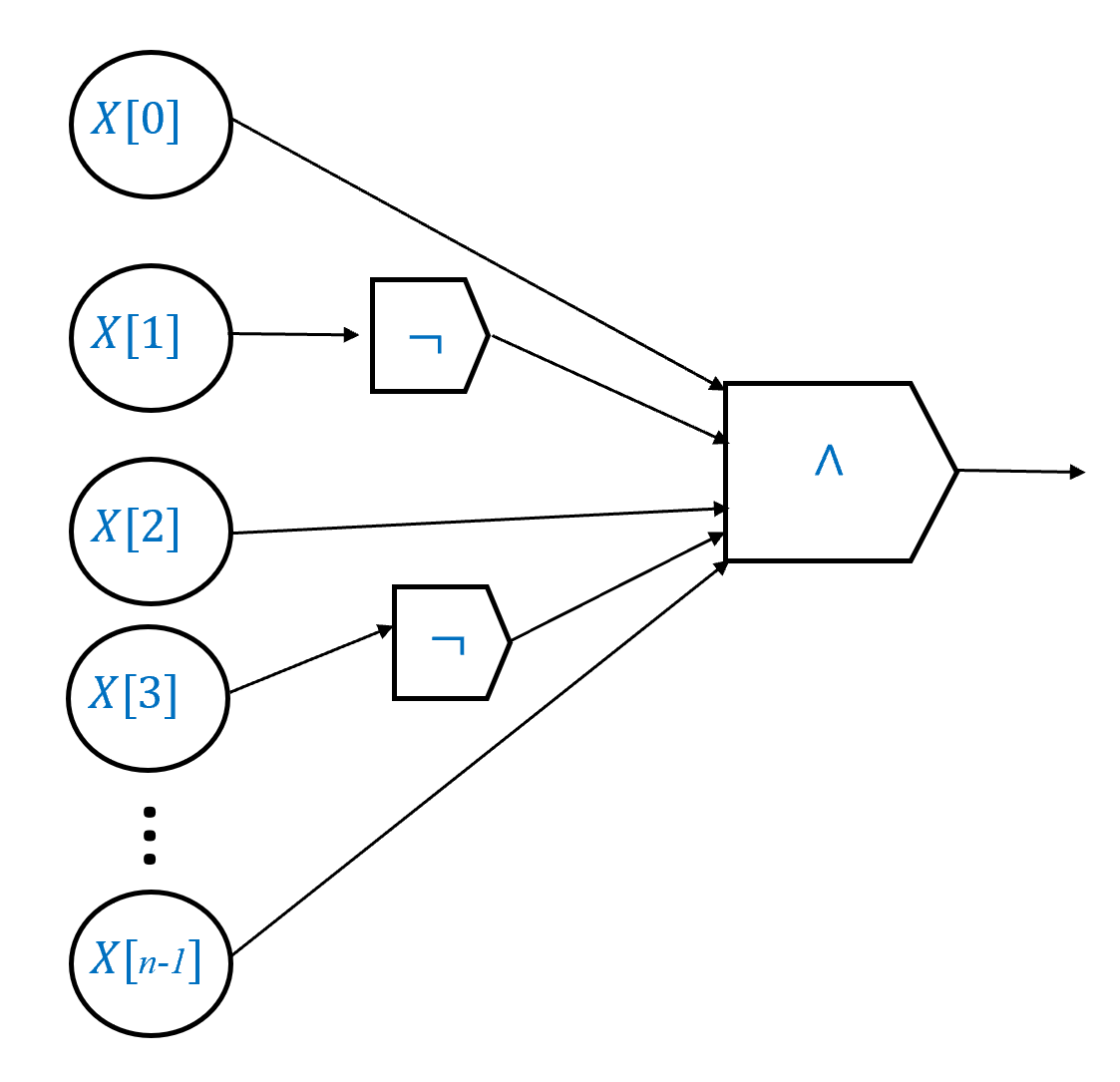
也就是说, 对于每个 当且仅当 的三个元素中至少有两个等于 时, 你能用 、 和 写出一个计算 的公式吗? (此处建议你先停下来自己推导公式. 提示: 虽然某些函数需要用到 但计算 不需要使用它. )
我们先用文字重新表述 “当且仅当存在一对不同的元素 且 和 都等于 时, “
换句话说, 当且仅当 且 , 或 且 , 或 且 .
由于三个条件 的 可以写作 我们可以将其翻译为如下公式:
回想一下, 我们也可以将 写作 将 写作 使用这种符号表示, 公式 (3.1) 也可以写作:
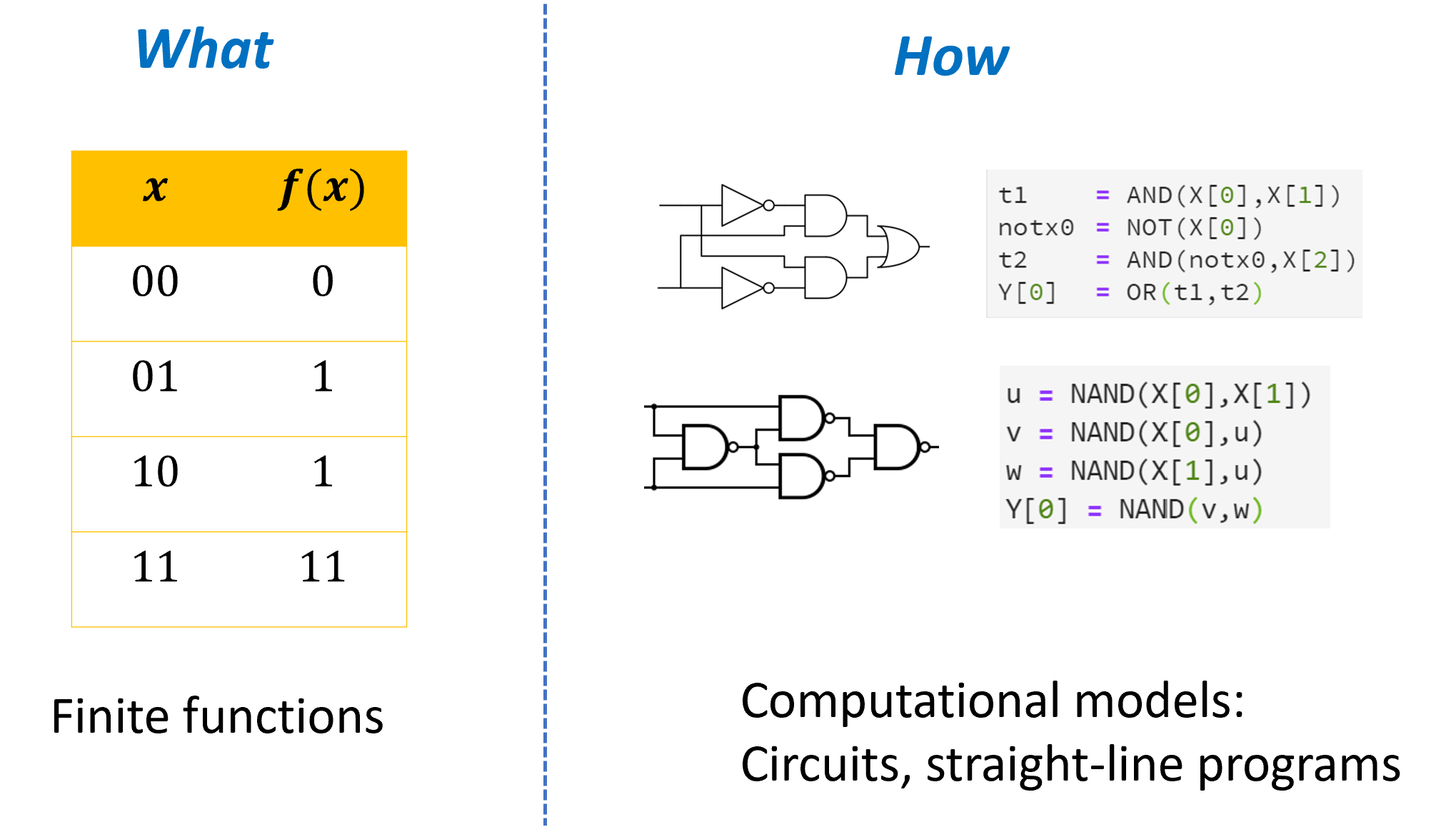
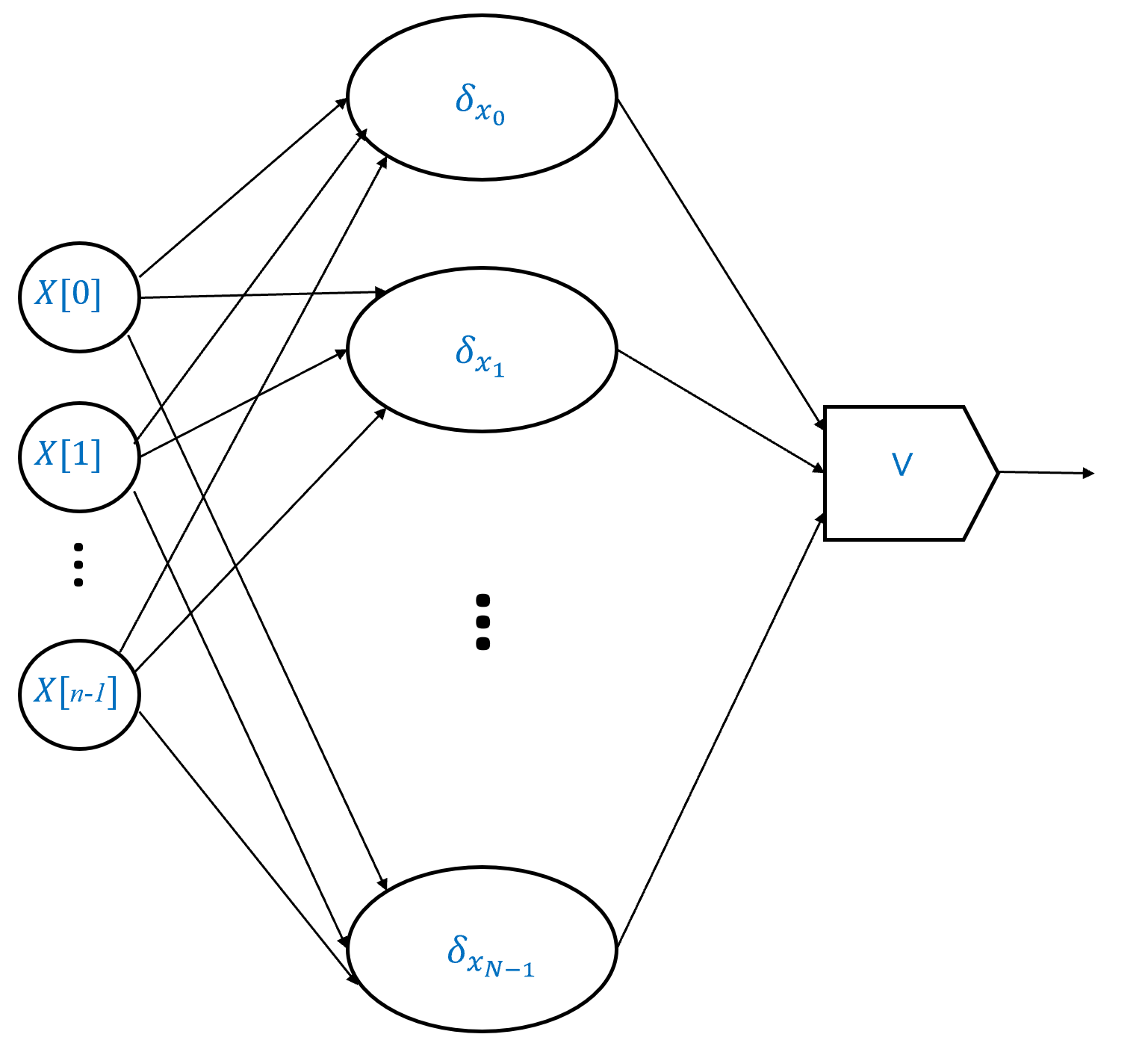
我们也可以将公式 (3.1) 以“编程语言“的形式表示: 将其表达为一组指令, 用于在给定基本操作 的情况下计算
def MAJ(X[0],X[1],X[2]):
firstpair = AND(X[0],X[1])
secondpair = AND(X[1],X[2])
thirdpair = AND(X[0],X[2])
temp = OR(secondpair,thirdpair)
return OR(firstpair,temp)
3.2.1 和 的一些性质
与标准的加法和乘法类似, 函数 和 满足交换律: 和 以及结合律: 和
于是如同加法和乘法的情况, 我们通常可以省略括号, 将 写作 对更多项的 和 同理.
它们还满足分配律的一种变体:
对练习 3.1的解答
对练习 3.1的解答
我们可以通过枚举 的所有 种可能取值来证明这一点, 但它也可以直接从标准的分配律推导出来.
假设我们将任意正整数视为“真“, 将零视为“假“. 那么对于每个数 为正当且仅当 为真, 而 为正当且仅当 为真.
这意味着对于每个 表达式 为真当且仅当 为正, 而表达式 为真当且仅当 为正.
根据标准的分配律 因此前者表达式为真当且仅当后者表达式为真.
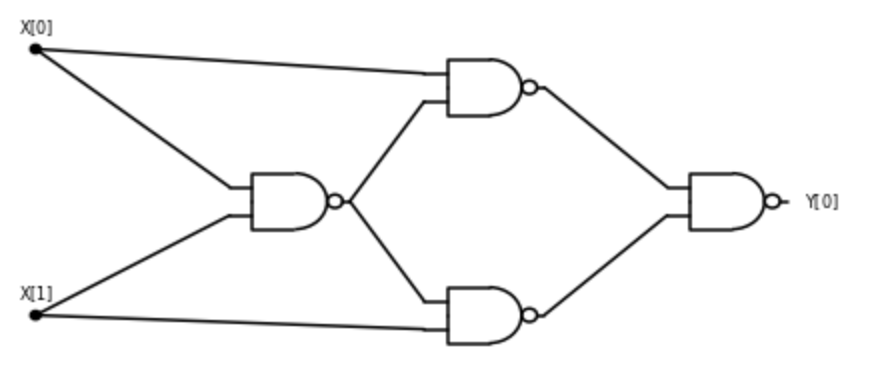
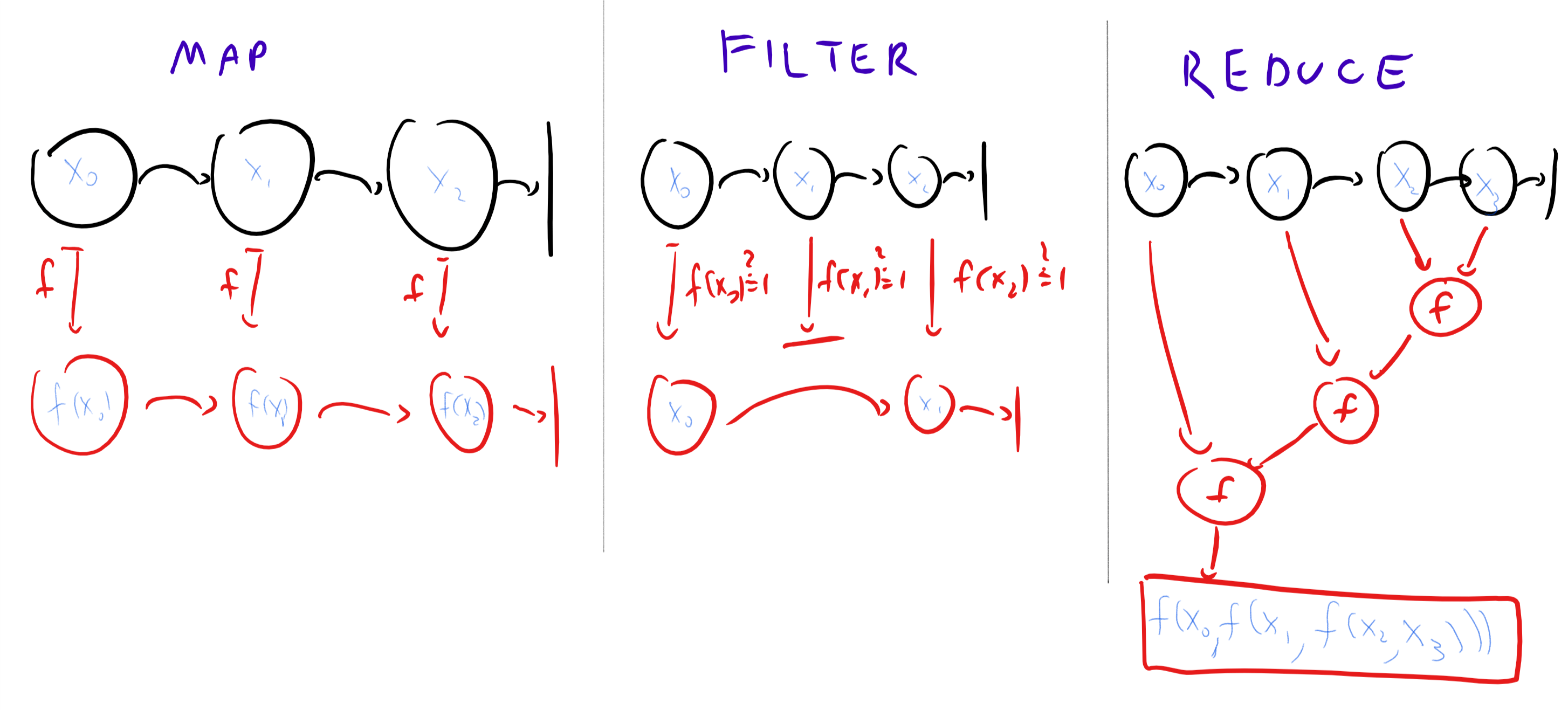
3.2.2 扩展例子: 计算异或(
让我们看看如何用方才的基本运算得到一种新运算. 定义 为函数 也就是说,
我们指出, 可以仅使用 、 和 来构造
以下算法使用 、 和 来计算
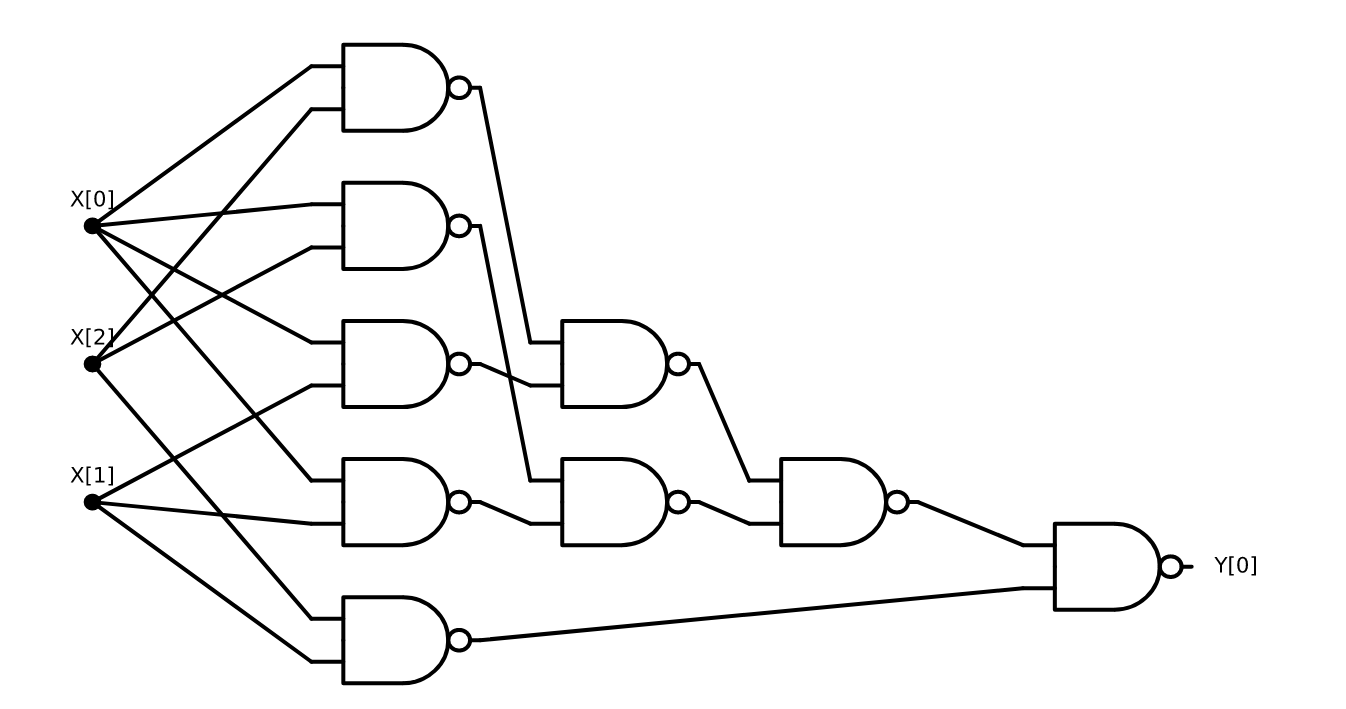
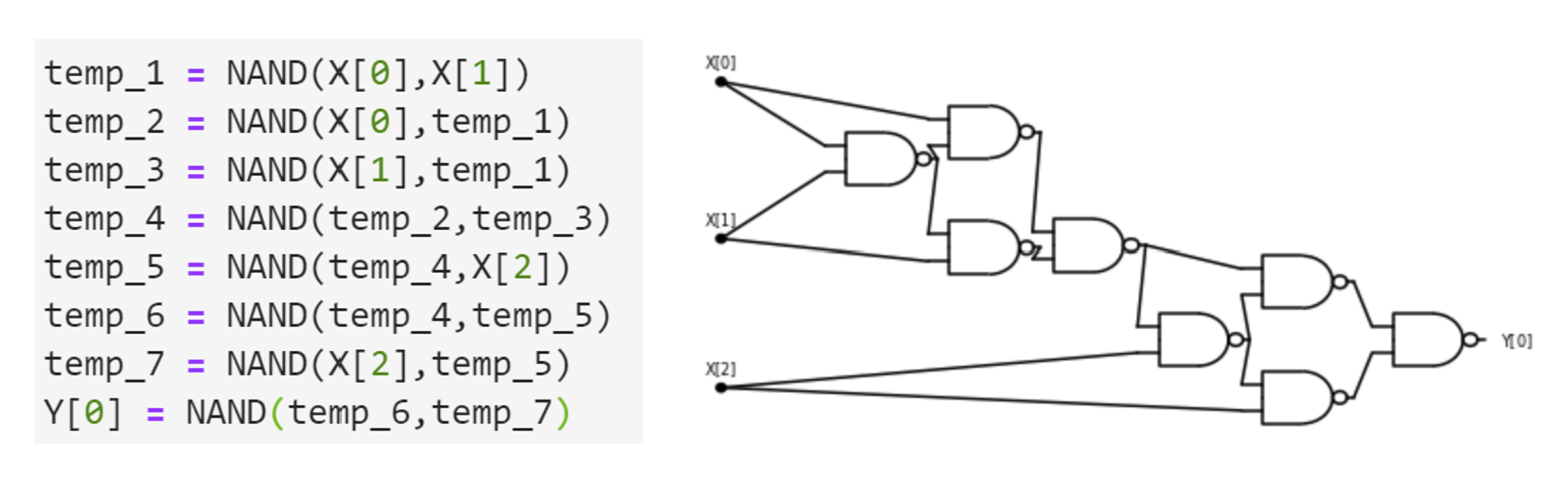
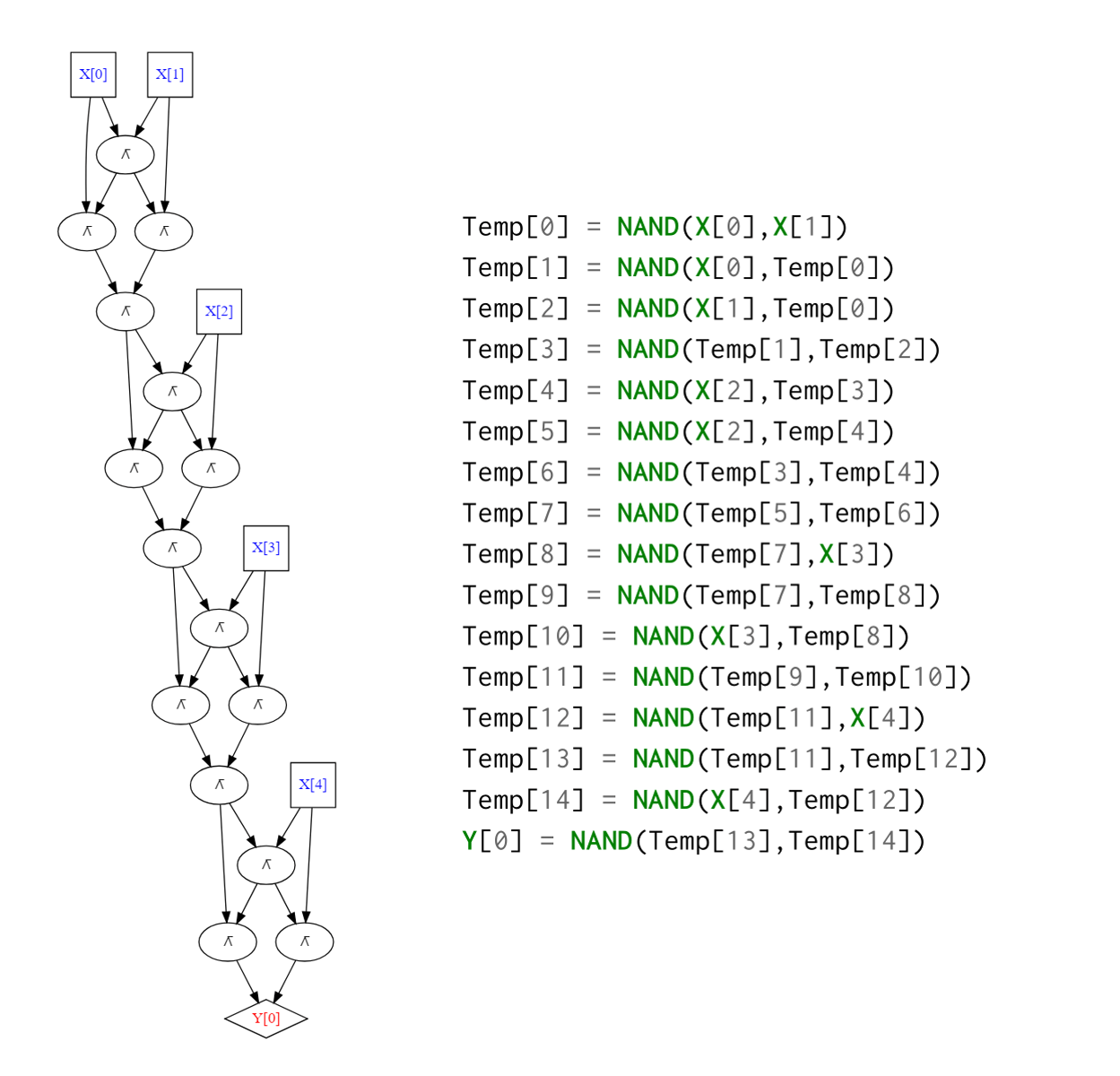
引理 3.1. 对于每个 在输入 时, 算法 3.1 输出
我们也可以用编程语言来描述 算法 3.1. 特别地, 以下是 函数的 Python 实现:
def AND(a,b): return a*b
def OR(a,b): return 1-(1-a)*(1-b)
def NOT(a): return 1-a
def XOR(a,b):
w1 = AND(a,b)
w2 = NOT(w1)
w3 = OR(a,b)
return AND(w2,w3)
# 一个测试
print([f"XOR({a},{b})={XOR(a,b)}" for a in [0,1] for b in [0,1]])
# ['XOR(0,0)=0', 'XOR(0,1)=1', 'XOR(1,0)=1', 'XOR(1,1)=0']
对练习 3.2的解答
对练习 3.2的解答
模 2 加法具有与通常加法相同的 结合律 ( 和 交换律 (
这意味着, 如果我们定义 那么
换句话说,
由于我们已经知道如何仅用 、 和 来计算 因此可以将其组合起来, 用同样的基本运算实现 在 Python 中, 这可以写作如下程序:
def XOR3(a,b,c):
w1 = AND(a,b)
w2 = NOT(w1)
w3 = OR(a,b)
w4 = AND(w2,w3)
w5 = AND(w4,c)
w6 = NOT(w5)
w7 = OR(w4,c)
return AND(w6,w7)
# 一个小测试
print([f"XOR3({a},{b},{c})={XOR3(a,b,c)}" for a in [0,1] for b in [0,1] for c in [0,1]])
# ['XOR3(0,0,0)=0', 'XOR3(0,0,1)=1', 'XOR3(0,1,0)=1', 'XOR3(0,1,1)=0', 'XOR3(1,0,0)=1', 'XOR3(1,0,1)=0', 'XOR3(1,1,0)=0', 'XOR3(1,1,1)=1']
3.2.3 非正式地定义“基本运算“和“算法“
我们已经看到, 通过组合应用 、 和 可以得到一些有趣的函数. 这启发我们将 、 和 视为我们的基本运算, 从而给出如下关于算法的定义:
-
首先, 这一定义确实过于非正式. 我们既没有精确说明每一步到底做了什么, 也没有明确“将 作为输入“究竟是什么意思.
-
其次, 选择 、 或 看起来相当任意. 为什么不是 和 ? 为什么不允许加法和乘法这样的运算? 又或者其他逻辑结构, 例如
if/then或while? -
第三, 我们是否确信该定义真的与实际计算有关? 如果有人给出了这种算法的描述, 我们是否真的能够在现实中用它来计算相应的函数?
本书的很大一部分内容将致力于回答上述问题. 我们将看到:
-
我们可以把算法的定义完全形式化, 从而为“算法 计算函数 “这样的表述赋予精确的数学含义.
-
虽然选择 / / 看似任意, 我们本可以选择其他函数, 但实际上这种选择影响不大. 我们会看到, 即使改用加法和乘法, 或者几乎任何可以合理视为基本步骤的操作, 我们依然能够得到相同的计算能力.
-
事实证明, 我们确实可以在现实世界中计算这种基于 / / 的算法. 首先, 这样的算法定义清晰, 因此人类可以用纸和笔逐步执行. 其次, 这种计算可以通过多种方式机械化. 我们已经看到, 可以编写 Python 程序来对应执行这样的指令序列. 而实际上, 还可以通过被称为晶体管的元件, 用电子信号直接实现 、 和 等操作. 这正是现代电子计算机的工作方式.
在本章余下的内容以及本书后续部分, 我们将开始回答这些问题. 我们会看到更多简单操作组合出复杂操作的实例, 包括加法、乘法、排序等. 同时, 我们还会讨论如何通过多种技术物理实现 、 和 等基本操作.
3.3 布尔电路
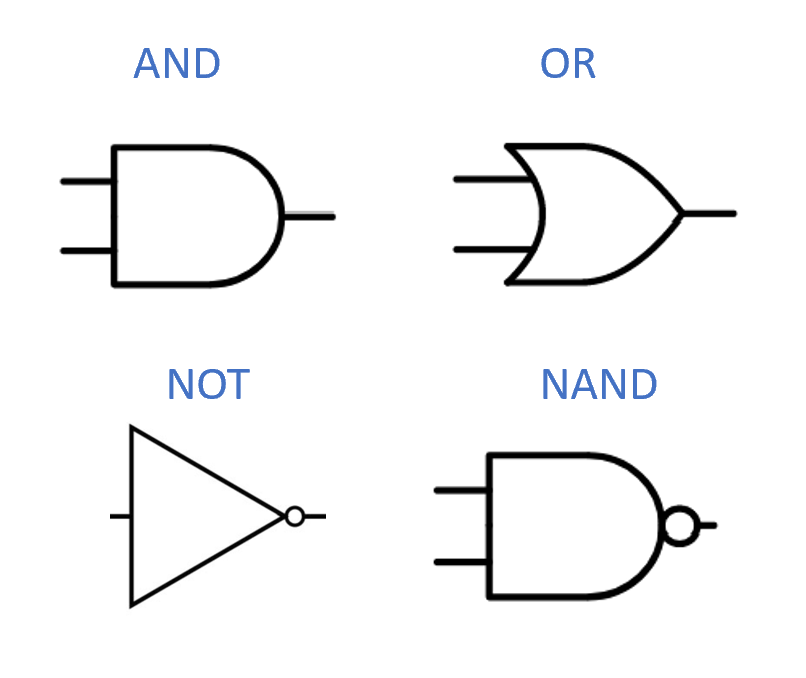
图 3.7. 逻辑运算或“门“的标准符号包括 、、 以及在3.6节中讨论的 运算.
布尔电路提供了“组合基本运算“的精确定义. 一个布尔电路 (参见图 3.9) 由门和输入组成, 并通过导线连接.
导线传递的信号表示值 或 每个门对应 、 或 运算. 一个 门有两条输入导线和一条或多条输出导线, 如果这两条输入导线的信号分别为 和 ( , 则输出导线上的信号为 和 门的定义类似.
输入端只有输出导线. 如果我们将某个输入设为 则该值会沿其所有输出导线传播. 我们还将一些门指定为输出门, 其值对应于电路的计算结果. 例如, 图 3.8 给出了一个用于计算 函数的电路, 参考 节3.2.2.
对于一个 输入的布尔电路 我们在输入端放置 的比特, 然后沿导线传播信号, 直到到达输出端, 从而完成电路的计算, 参见 图 3.9.
对练习 3.3的解答
对练习 3.3的解答
另一种描述函数 的方式是: 当且仅当输入 满足 或 时, 它输出
我们可以将条件 表述为 这可以用三个 门计算.
同样地, 我们可以将条件 表述为 这可以用四个 门和三个 门计算.
的输出是这两个条件的 由此得到的电路包含 4 个 门、6 个 门和 1 个 门, 如图 3.10所示.
3.3.1 布尔电路: 形式化定义
我们之前非正式地将布尔电路定义为通过导线连接 、 和 门, 从输入生成输出的电路.
然而, 为了能够证明关于计算各种函数的布尔电路存在性或非存在性的定理, 我们需要:
- 将布尔电路作为数学对象进行形式化定义.
- 正式定义电路 计算函数 的含义.
接下来我们将进行这一定义. 我们把布尔电路定义为带标记的有向无环图 (DAG) . 图的顶点对应电路的门和输入端, 图的边对应导线. 电路中从输入或门 到门 的导线对应顶点间的有向边. 输入顶点没有入边, 而每个门根据其计算的函数具有适当数量的入边 (即 和 门有两个入邻居, 门有一个入邻居) .
正式定义如下 (参见图 3.11) :
定义 3.3 (布尔电路). 设 为正整数, 且 一个具有 个输入、 个输出和 个门的布尔电路是一个带标记的有向无环图 (DAG) 其顶点数为 满足以下性质:
-
恰好有 个顶点没有入邻居. 这些顶点称为输入端, 标记为 每个输入端至少有一个出邻居.
-
其余 个顶点称为门. 每个门标记为 、 或 标记为 ( 或 ( 的门有两个入邻居, 标记为 ( 的门有一个入邻居. 允许存在平行边. ^[平行边意味着 AND 或 OR 门 的两个入邻居可以是同一个门 由于对任意 有 在仅使用 AND/OR/NOT 门的电路中, 这类平行边并不会计算出新的值. 但在后面引入更一般门集合时, 我们将看到平行边的用途. ]
-
恰好有 个门同时标记为 (除了其本来的 // 标记之外) , 称为输出端.
布尔电路的规模定义为其包含的门的数量
这是一个非平凡的数学定义, 因此值得慢慢仔细阅读.
正如所有数学定义一样, 我们使用已知的数学对象–**有向无环图 (DAG) **–来定义一个新的对象, 即布尔电路.
此时复习一些 DAG 的基本性质会很有帮助, 特别是它们可以进行拓扑排序的事实, 参见1.6节.
如果 是一个具有 个输入和 个输出的布尔电路, 且 则自然可以计算 在输入 的输出:
将输入顶点 赋值为 然后对每个门应用其入邻居的值, 最后输出对应于输出顶点的值.
形式化定义如下:
定义 3.4 (利用布尔电路计算函数).
设 为一个具有 个输入和 个输出的布尔电路.
对于每个 在输入 上的 输出, 记作 定义为以下过程的结果:
我们令 为 的 最小分层 (又称 拓扑排序, 见定理1.26) .
令 为 的最大层数, 对每个 执行以下操作:
-
对每个位于第 层的顶点 (即 满足 执行:
-
如果 是输入顶点, 标记为
X[i], 其中 则将 赋值给 -
如果 是标记为 的门顶点, 且有两个入邻居 则将 和 的值的 赋给 (由于 和 是 的入邻居, 它们位于比 更低的层, 因此它们的值已经被赋值. )
-
如果 是标记为 的门顶点, 且有两个入邻居 则将 和 的值的 赋给
-
如果 是标记为 的门顶点, 且有一个入邻居 则将 的值取反并赋给
-
-
该过程的结果是一个 其中对于每个 为标记为
Y[j]的顶点的值.
设 如果对于每个 都有 则称电路 计算 函数
在表述 定义 3.3 时, 我们做了一些技术性的选择, 这些选择并不是非常重要, 但对我们后续会很方便.
允许存在平行边意味着一个 或 门 可以让它的两个入邻居都是同一个门
由于对每个 都有 因此在仅使用 门的电路中, 这类平行边并不会带来新的计算值.
然而, 我们稍后会看到包含更一般门集合的电路.
要求每个输入顶点至少有一个出邻居也不是特别重要, 因为我们总可以添加“虚拟门“来使用这些输入.
不过这个要求很方便, 因为它保证了 (由于每个门最多有两个入邻居) 电路中的输入数量永远不会超过其规模的两倍.
3.4 直线程序
我们已经看到两种使用 、 和 来计算函数 的方式:
-
布尔电路, 在 定义 3.3 中定义, 通过将 、 和 门通过导线连接到输入来计算
-
我们也可以使用 直线程序 来描述这样的计算, 该程序的每一行形式为
foo = AND(bar,blah)、foo = OR(bar,blah)和foo = NOT(bar), 其中foo、bar和blah是变量名. (称其为 直线程序, 因为它不包含循环或分支 (例如 if/then) 语句. )
为了更精确地描述第二种定义, 我们现在定义一种与布尔电路等价的 编程语言.
我们将这种编程语言称为 AON-CIRC 编程语言 (“AON” 代表 “CIRC” 代表 circuit) .
例如, 以下是一个 AON-CIRC 程序, 对于输入 输出 (即对 应用 操作) :
temp = AND(X[0],X[1])
Y[0] = NOT(temp)
AON-CIRC 并不是一种实用的编程语言: 它仅用于教学目的, 用来将计算建模为 、 和 的组合. 然而, 它仍然可以很容易地在计算机上实现.
根据这个例子, 你可能已经能够猜到如何编写程序来计算 (例如) 以及更一般地, 如何将布尔电路翻译为 AON-CIRC 程序. 但是, 由于我们希望对 AON-CIRC 程序证明数学性质, 我们需要精确定义 AON-CIRC 编程语言.
编程语言的精确定义有时可能冗长且枯燥, 例如, C 语言规范 就超过 500 页. 但对于安全可靠的实现至关重要. 幸运的是, AON-CIRC 编程语言足够简单, 我们可以相对轻松地对其进行正式定义.
3.4.1 AON-CIRC 编程语言规范
一个 AON-CIRC 程序是一系列字符串, 我们称之为“行“, 满足以下条件:
-
每一行具有以下形式之一:
foo = AND(bar,baz)、foo = OR(bar,baz)或foo = NOT(bar), 其中foo、bar和baz是 变量标识符. (我们遵循常见的 编程语言惯例, 使用foo、bar、baz等名称作为通用标识符的示例. )
行foo = AND(bar,baz)对应于将变量foo赋值为变量bar和baz的逻辑 类似地,foo = OR(bar,baz)和foo = NOT(bar)分别对应逻辑 和逻辑 操作. -
AON-CIRC 编程语言中的 变量标识符 可以由字母、数字、下划线和方括号的任意组合构成. 有两类特殊变量:
- 形式为
X[i]的变量, 其中 称为 输入变量. - 形式为
Y[j]的变量, 称为 输出变量.
- 形式为
-
一个有效的 AON-CIRC 程序 包含输入变量
X[0],X[n-1]和输出变量Y[0],Y[m-1], 其中 为自然数. 我们称 为程序 的 输入数, 为 输出数. -
在有效的 AON-CIRC 程序中, 每一行右侧的变量必须是输入变量或在之前的行中已经被赋值的变量.
-
若 是一个具有 个输入和 个输出的有效 AON-CIRC 程序, 则对于每个 程序 在输入 上的 输出 是字符串 定义如下:
- 将输入变量
X[0],X[n-1]初始化为 - 按顺序逐行执行 的操作行, 在每行中将左侧变量赋值为右侧操作的结果.
- 执行结束后, 令 为输出变量
Y[0],Y[m-1]的值.
- 将输入变量
-
我们用 表示程序 在输入 上的输出.
-
AON-CIRC 程序 的 规模 是它包含的行数. (读者可能注意到, 这与我们定义的电路规模–门的数量–是一致的. )
现在我们已经正式定义了 AON-CIRC 程序的规范, 就可以定义 AON-CIRC 程序 计算一个函数 的含义:
以下已解练习给出了一个 AON-CIRC 程序的示例.
对练习 3.4的解答
对练习 3.4的解答
编写这样的程序虽然繁琐, 但并不困难. 比较两个数字时, 我们首先比较它们的最高有效位, 然后依次比较下一位, 以此类推. 在数字仅有两位二进制的情况下, 这些比较特别简单. 由 表示的数字大于由 表示的数字, 当且仅当满足以下任一条件:
- 的最高有效位 大于 的最高有效位
或
- 两个最高有效位 和 相等, 但
另一种等价表述为: 数字 大于 当且仅当 或 ( 且
对于二进制位 条件 仅当 且 也就是 条件 则为
结合这些观察, 可以得到用于计算 的以下 AON-CIRC 程序:
# Compute CMP:{0,1}^4-->{0,1}
# CMP(X)=1 iff 2X[0]+X[1] > 2X[2] + X[3]
temp_1 = NOT(X[2])
temp_2 = AND(X[0],temp_1)
temp_3 = OR(X[0],temp_1)
temp_4 = NOT(X[3])
temp_5 = AND(X[1],temp_4)
temp_6 = AND(temp_5,temp_3)
Y[0] = OR(temp_2,temp_6)
我们也可以将这个 8 行程序表示为一个包含 8 个门的电路, 见图 3.12.
3.4.2 证明AON-CIRC程序与布尔电路的等价性
我们现在正式证明 AON-CIRC 程序和布尔电路具有完全相同的计算能力:
证明思路很简单–AON-CIRC 程序和布尔电路只是描述同一计算过程的不同方式.
例如, 布尔电路中的一个 门对应于对两个已计算值执行 操作.
在 AON-CIRC 程序中, 这对应于一行将两个已计算变量的 结果存储到一个变量中的语句.
对定理 3.1的证明
对定理 3.1的证明
设 由于该定理是**“当且仅当”**的命题, 要证明它, 我们需要展示两个方向:
- 将计算 的 AON-CIRC 程序转换为计算 的布尔电路;
- 将计算 的布尔电路转换为计算 的 AON-CIRC 程序.
我们先考虑第一个方向. 设 是一个计算 的 AON-CIRC 程序. 我们定义一个电路 如下: 该电路有 个输入和 个门. 对于每个 若第 行运算为 foo = AND(bar,blah), 则电路中的第 个门为 门, 其入邻居连接到对应的第 和第 个门, 和 分别对应于在第 行之前最后一次写入变量 bar 和 blah 的行号. (例如, 如果 且 bar 最近一次被写入的是第 行, blah 最近一次被写入的是第 行, 则门 的两个入邻居为门 和门 )
如果 bar 或 blah 是输入变量, 则将门连接到对应的输入顶点.
如果 foo 是输出变量 (形式为 Y[j]) , 则在对应门上添加相同标签, 将其标记为输出门.
对于 或 操作的情况也类似, 只是使用对应的 或 门, 并且 门只有一个入邻居.
对于任意输入 若运行程序 第 行计算的值恰好等于在电路 上对 求值时第 个门的值. 因此, 对所有 有
再看另一个方向. 设 是一个具有 个输入、 个门的电路, 计算函数 我们对门按照拓扑序排序, 记为
现在可以构造一个包含 行运算的程序
对于每个 若 是一个 门, 其入邻居为 则在 中添加一行 temp_i = AND(temp_j,temp_k), 除非某个顶点是输入顶点或输出门, 此时改用 X[.] 或 Y[.].
由于我们按照拓扑顺序操作, 保证入邻居 和 对应的变量已被赋值.
和 门同理.
再次验证, 对于每个输入 因此程序计算与电路相同的函数.
(注意, 由于 是合法电路, 根据 定义 3.3, 的每个输入顶点至少有一个出邻居, 并且恰有 个输出门标记为 因此所有变量 X[0],\ldots,X[n-1] 和 Y[0],\ldots,Y[m-1] 都会出现在程序 中. )
3.5 计算设备的物理实现 (插曲)
计算是一个抽象概念, 它并不等同于其物理实现.
虽然大多数现代计算设备是通过将逻辑门映射到基于半导体的晶体管实现的, 但纵观历史, 人类曾经使用过各种各样的机制来进行计算, 包括机械系统、气体与液体 (称为流体计算) 、生物和化学过程, 甚至是生物体本身 (参见图 3.14或这个视频, 了解螃蟹或黏菌如何被用于计算) .
在本节中, 我们将回顾这些实现方式, 以帮助理解如何能够将布尔电路直接转化为物理世界中的系统, 而无需经过体系结构、操作系统和编译器的完整抽象层. 同时, 这也强调了基于硅的处理器绝不是实现计算的唯一方式.
事实上, 正如我们将在第23章 中看到的, 一个令人兴奋的研究方向是使用不同的介质来进行计算, 从而利用量子力学效应来实现全新的算法类型.
Such a cool way to explain logic gates. pic.twitter.com/6Wgu2ZKFCx
— Lionel Page (\@page_eco) 2019年10月28日
3.5.1 晶体管
晶体管 (transistor) 可以看作是一个具有两个输入和一个输出的电路: 输入称为源极 (source) 和栅极 (gate) , 输出称为漏极 (sink) .
栅极决定了电流是否能够从源极流向漏极.
- 在标准晶体管中, 如果栅极处于“开 (ON) “状态, 则电流可以从源极流向漏极; 如果栅极处于“关 (OFF) “状态, 则电流无法流动.
- 在互补晶体管中, 情况正好相反: 栅极“关“时允许电流流动, 而栅极“开“时则不允许.
实现晶体管逻辑的方法有很多. 例如, 可以通过水压与水龙头的开合来模拟晶体管的工作 (见图 3.15) . 这似乎只是个小趣味, 但事实上有一个名为流体计算 (fluidics) 的研究领域, 专门研究如何利用液体或气体实现逻辑运算. 其动机之一是在极端环境 (如太空或战场) 中工作, 因为在这些环境下常规电子设备可能无法存活.
晶体管的标准实现是通过电流. 而最早的实现方式之一是真空管. 顾名思义, 真空管是一个内部抽空的管子, 电子可以自由地从源 (电丝) 流向漏 (金属板) . 但在它们之间有一个“栅极“ (网格) , 通过调节其电压可以阻止电子的流动.
早期真空管大约有灯泡那么大 (外形也很像灯泡) . 到 1950 年代, 它们被晶体管取代. 晶体管利用半导体实现相同的逻辑. 半导体在正常情况下不导电, 但通过掺杂 (doping) 以及施加外部电场, 可以调控其导电性 (即场效应) .
进入 1960 年代后, 计算机开始使用集成电路 (integrated circuits) , 极大提高了晶体管的集成密度. 1965 年, 戈登·摩尔 (Gordon Moore) 预测集成电路中晶体管的数量大约每年会翻一番 (见图 3.16) . 他还推测这将带来“诸如家庭计算机–或至少是接入中央计算机的终端–、汽车的自动控制, 以及个人便携通信设备等奇迹“.
从那时起, 经调整后的“摩尔定律“基本上一直成立, 尽管指数级增长不可能无限持续, 一些物理极限已经逐渐显现.
3.5.2 由晶体管到逻辑门
我们可以使用晶体管来实现各种布尔函数, 例如 、 和
对于每一个二输入门 其实现方式是一个具有两个输入导线 和一个输出导线 的系统. 若我们将高电压视为““, 低电压视为”“, 那么当且仅当 时, 导线 的值为”“ (参见下列图 3.19 和图 3.20) .
这意味着: 如果存在一个 电路可以计算函数 那么我们也可以在物理世界中通过晶体管来计算
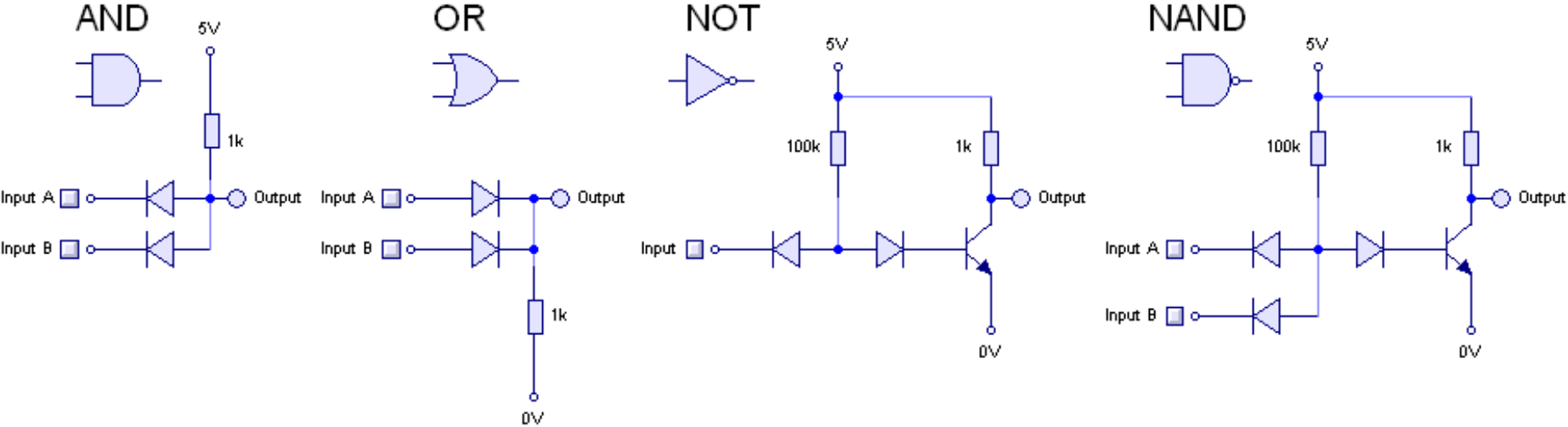
图 3.19. 使用晶体管实现逻辑门. 图源自 Rory Mangles 的网站.
图 3.20. 使用晶体管实现 门 (参见 3.6节) .
3.5.3 生物计算
计算也可以基于生物或化学系统. 例如, lac 操纵子 仅在条件 成立时才会产生消化乳糖所需的酶, 其中 表示“存在乳糖“, 表示“存在葡萄糖“.
研究人员已经成功制造出基于 DNA 分子的晶体管, 并由此构建逻辑门 (参见图 3.21) . 诸如 Cello 编程语言 这样的项目, 能够将布尔电路转换为 DNA 序列, 从而在细菌细胞中执行运算 (参见该视频) .
DNA 计算的动机之一是实现更高的并行性或存储密度; 另一个动机是创造“智能生物因子“, 这些因子或许能够被注入体内, 自我复制, 并修复或杀死因癌症等疾病损伤的细胞.
当然, 生物系统中的计算不仅限于 DNA: 甚至更大规模的系统, 例如鸟群, 也可以被视为计算过程.
图 3.21. 基于 DNA 的逻辑门性能. 图源自 Bonnet 等人, Science, 2013.
3.5.4 元胞自动机和生命游戏(GoL)
元胞自动机是一种由一系列细胞组成的系统模型, 每个细胞都可以处于有限的状态之一.
在每一步中, 细胞会根据其邻居细胞的状态以及一些简单规则来更新自身状态.
正如我们将在本书后续部分讨论的那样 (参见 第8.4节) , 元胞自动机 (例如康威的“生命游戏“) 可以用来模拟计算门.
图 3.22. 利用“生命游戏“配置实现的 AND 门. 图源自 Jean-Philippe Rennard 的论文.
3.5.5 神经网络
我们每个人都随身携带的一种计算设备就是我们自己的大脑. 大脑在人类历史上一直发挥作用, 从区分猎物与捕食者, 到进行科学发现和艺术创作, 再到写出精巧的 280 字短消息. 大脑的确切工作机制仍未完全被理解, 但一种常见的数学模型是 (非常庞大的) 神经网络.
神经网络可以看作布尔电路, 只是它并非以 / / 为基本门, 而是使用其他类型的基本门. 例如, 一种可以使用的基是阈值门.
对于每个整数向量 和整数 (其中一些分量可以为负) , 定义对应的阈值函数 为: 当且仅当 时, 输入 被映射为
例如, 向量 与阈值 所对应的 就是 上的多数函数 阈值门可以看作对构成人类与动物大脑核心的神经元的一种近似. 粗略来说, 一个神经元有 个输入和一个输出, 当这些信号的强度超过某个阈值时, 神经元就会“触发“或“激活“其输出.
许多机器学习算法采用的人工神经网络并非旨在模仿生物学, 而是为了执行某些计算任务, 因此它们并不局限于阈值门或其他生物学启发的门. 通常来说, 神经网络的输入信号被视为实数而非 值, 并且一个门的输出是通过计算 得到的, 其中 是某种激活函数, 例如修正线性单元 (ReLU) 、Sigmoid 或其他函数 (见图 3.23) .
不过, 就我们讨论的范围而言, 上述所有模型在本质上是等价的 (参见 习题 3.13) . 特别是, 我们可以通过二进制表示实数并将对应权重乘以 的方式, 将实数输入化为二进制输入.
图 3.23. 神经网络中常用的激活函数, 包括修正线性单元 (ReLU) 、Sigmoid 和双曲正切. 它们都可以看作阶跃函数的连续近似形式. 所有这些函数都能用来计算 门 ( 习题 3.13) . 这一性质使得神经网络 (近似地) 能够计算任何布尔电路可计算的函数.
3.5.6 利用弹珠和管道搭建的计算机
我们可以利用许多其他物理介质来实现计算, 而无需任何电子、生物或化学组件. 人们曾经提出许多关于机械计算机的构想, 至少可以追溯到 1670 年代 Gottfried Leibniz 的计算机, 以及 Charles Babbage 1837 年提出的机械“分析机“计划.
打个比方, 图 3.24 展示了使用弹珠通过管道来实现 ( 的取反, 参见 3.6节) 门的简单方法. 我们通过一对管道表示逻辑值 保证恰好有一颗弹珠在其中一条管道中流动. 将其中一条管道称为“ 管“, 另一条管道称为“ 管“, 弹珠所在管道的身份决定逻辑值.
一个 门对应一个机械装置, 具有两对输入管道和一对输出管道, 使得对于每个 如果两颗弹珠分别沿第一对管道的 管和第二对管道的 管滚向装置, 那么弹珠将沿输出对中对应 的管道滚出.
事实上, 市面上还有一个以弹珠为计算基础的教育游戏, 参见下方的图 3.26.

图 3.26. 游戏 “Turing Tumble” 中使用弹珠实现逻辑门.
3.6 NAND函数
函数是另一个非常简单且在定义计算中极为有用的函数.
它是一个将 映射到 的函数, 定义为:
顾名思义, 是 AND 的取反 (即 , 因此显然可以使用 和 来计算
有趣的是, 反过来我们也有:
对定理 3.2的证明
对定理 3.2的证明
我们从以下观察开始. 对于每个 有
因此,
这意味着 可以计算
根据“双重否定“原理, 因此我们也可以使用 来计算
一旦我们能够计算 和 就可以利用de Morgan定律计算
(也可以写作 , 对每个 都成立.
定理 3.2 的证明非常简单, 但你应当确保 (1) 你理解该定理的陈述, 且 (2) 你能够读懂其证明过程. 尤其要理解为什么de Morgan定律成立.
我们可以使用 来计算许多其他函数, 如以下练习所示.
对练习 3.5的解答
对练习 3.5的解答
3.6.1 电路
我们将 电路 定义为所有逻辑门均为 运算的电路.
这样的电路同样对应一个有向无环图 (DAG) , 因为所有逻辑门都执行相同的功能 (即 , 因此甚至无需对它们进行标记, 并且所有逻辑门的入度都恰好为 2.
尽管形式简单, 电路却具有相当强大的能力.
事实上, 我们可以证明以下定理:
对定理 3.3的证明
对定理 3.3的证明
如果 是一个布尔电路, 那么由于我们在 定理 3.2 的证明中已经看到, 对于任意 有:
因此, 我们可以将 中的每一个逻辑门替换为至多三个 门, 从而得到一个等价电路
由此得到的电路至多包含 个逻辑门.
3.6.2 更多 电路的例子 (选读)
下面给出一些更复杂的 电路示例:
后继数: 考虑如下任务: 输入一个字符串 它表示一个自然数 我们希望计算 换句话说, 我们希望计算函数
使得对于任意 有 并且满足
(为了书写简洁, 在此示例中我们采用最低有效位在前而不是在后的表示方式. )
后继操作可以非正式地描述为: “将 加到最低有效位并向高位传递进位”.
更准确地说, 在二进制表示的情形下, 要得到 的后继, 我们从最低有效位开始扫描 把所有的 翻转为 直到遇到一个等于 的比特, 把它翻转为 并停止.
因此, 我们可以通过以下步骤来计算 的后继:
算法 3.2 精确描述了如何计算后继, 并且可以很容易地转化为执行相同计算的 Python 代码, 但它似乎不能直接生成一个计算该运算的 电路.
然而, 我们可以逐行将该算法转换为 电路.
例如, 由于对任意 都有 我们可以将最初的语句 替换为
我们已经知道如何用 实现 因此可以用它来实现操作
类似地, 可以将 “if” 语句写作 也就是
最后, 赋值 可以写作
结合这些观察, 对于任意 我们就得到了一个计算 的 电路.
例如, 图 3.29展示了 时该电路的样子.
从自增到加法
一旦有了自增运算, 我们当然可以通过重复自增来计算加法 (即通过对 执行 次 来计算 . 然而, 这种方法既低效又没有必要.
利用同样的进位跟踪思想, 我们可以实现“中学“加法算法, 并计算函数 其在输入 时输出由 与 所表示的两个数之和的二进制表示:
同样地, 算法 3.3 可以被转换为 电路.
关键的观察是, “if/then” 语句实际上对应于 而我们在 练习 3.5 中已经看到函数 可以用 实现.
3.6.3 编程语言 NAND-CIRC
正如我们为布尔电路所做的那样, 我们可以定义 NAND 电路对应的编程语言.
它甚至比 AON-CIRC 语言更简单, 因为这里只有一种操作.
我们将 NAND-CIRC 编程语言 定义为这样一种编程语言, 其中每行 (除了输入/输出声明外) 具有以下形式:
foo = NAND(bar,blah)
其中 foo, bar 和 blah 指代变量.
形式上, 就像我们在 定义 3.5 中对 AON-CIRC 所做的那样, 我们可以以自然的方式定义 NAND-CIRC 程序的计算概念:
和之前一样, 我们可以证明 NAND 电路与 NAND-CIRC 程序是等价的 (见图 3.30).
我们省略 定理 3.4 的证明, 因为其思路与布尔电路与 AON-CIRC 程序等价的证明完全相同 (参见 定理 3.1) .
根据 定理 3.3 和 定理 3.4, 我们知道可以将任意 行的 AON-CIRC 程序 翻译为一个等价的 NAND-CIRC 程序, 行数最多为
实际上, 这种翻译可以通过将每一行 foo = AND(bar,blah)、foo = OR(bar,blah) 或 foo = NOT(bar) 替换为使用 NAND 的等价 1-3 行来轻松完成.
我们的 GitHub 仓库 提供了“代码证明“: 一个简单的 Python 程序 AON2NAND, 可以将 AON-CIRC 转换为等价的 NAND-CIRC 程序.
你可能听说过“图灵完备 (Turing Complete) “这一术语, 有时用来描述编程语言. (如果没听过, 可以忽略本备注的其余部分: 我们将在 第七章 中给出精确定义. )
如果听说过, 你可能会好奇 NAND-CIRC 编程语言是否具备这一属性. 答案是否定的, 或者更准确地说, “图灵完备“这个术语并不真正适用于 NAND-CIRC 编程语言.
原因在于, 根据设计, NAND-CIRC 编程语言只能计算有限函数 这些函数接受固定数量的输入比特并产生固定数量的输出比特. “图灵完备“这一术语仅适用于可以处理任意长度输入的无限函数的编程语言.
在本书后续章节中, 我们将回到这一区分进行进一步讨论.
3.7 上述所有模型的等价性
如果我们将 定理 3.1、定理 3.3 和 定理 3.4 结合起来, 可得到以下结论:
对定理 3.5的证明思路
对定理 3.5的证明思路
定理 3.1 是一个更一般结果的特例.
我们可以考虑更一般的计算模型, 其中不仅使用 AND/OR/NOT 或 NAND, 还可以使用其他运算 (参见第3.7.1节) . 事实证明, 布尔电路在计算能力上与这些模型也是等价的.
所有这些不同的计算定义方式最终导致等价模型, 这表明我们“走在正确的道路上“. 它证明了我们选择 AND/OR/NOT 或 NAND 作为基本操作的看似任意的选择是合理的, 因为这些选择并不影响计算模型的能力. 像 定理 3.5 这样的等价结果意味着我们可以轻松地在布尔电路、NAND 电路、NAND-CIRC 程序等之间进行转换. 在本书后续内容中, 我们将经常利用这一能力, 通常会根据方便选择最合适的表述, 而不会过分纠结. 因此, 我们不会过于担心例如布尔电路与 NAND-CIRC 程序之间的区别.
相比之下, 我们将继续特别注意区分电路/程序与函数 (回忆 重要提示 2.2) .
一个函数对应于计算任务的规范, 它本质上不同于程序或电路, 后者对应于任务的实现.
3.7.1 基于其它门集合的电路
或 并没有什么特别之处. 对于任意函数集合 我们可以定义使用 中元素作为门的电路的概念, 以及一个“ 编程语言“的概念, 其中每一行都将一个变量 foo 赋值为对某个 应用于先前定义的变量或输入变量的结果.
具体而言, 我们可以做如下定义:
AON-CIRC 程序对应于 程序, NAND-CIRC 程序对应于仅包含 函数的 程序, 但我们也可以定义 程序 (见下文) , 或者使用任意其他集合.
我们还可以定义 电路, 它是一个有向图, 其中每个 门 对应于应用某个 的操作, 每个门有 条入边和一条出边. (如果函数 不是对称的, 即输入顺序会影响结果, 那么我们需要标记每条入边对应函数的哪个参数. )
正如在 定理 3.1 中, 我们可以证明 电路与 程序是等价的.
我们已经看到, 对于 生成的电路/程序在计算能力上等价于 NAND-CIRC 编程语言, 因为我们可以用 // 计算 反之亦然.
这实际上是一个更一般现象的特例– 和其他门集的通用性–我们将在本书后续章节中深入探讨.
也存在一些计算能力更受限的集合
例如, 可以证明, 如果我们只使用 或 门 (不使用 , 则无法得到等价的计算模型.
练习中提供了几个通用门集与非通用门集的示例.
3.7.2 规范 vs. 实现 (再次强调)
正如我们在 第2.6.1节 中讨论的, 本书中最重要的区别之一是规范与实现的区分, 即分离“做什么“和“如何做“ (见图 3.31) .
一个 函数 对应于计算任务的规范, 即对于每个特定输入应该产生什么输出.
一个 程序 (或电路, 或其他任何用于指定算法的方式) 对应于实现, 即如何从输入计算所需输出.
也就是说, 程序是一组从输入计算输出的指令.
即便在同一个计算模型内, 也可能有多种不同方式来计算同一个函数. 例如, 计算多数函数的 NAND-CIRC 程序不止一个, 计算加法函数的布尔电路也不止一个, 等等.
混淆规范与实现 (或等价地, 函数与程序) 是一个常见错误, 而编程语言中常将程序部分称为“函数“也在一定程度上助长了这种误解. 然而, 在计算机科学的理论与实践中, 保持这一区别非常重要, 本书尤其重视这一点.
- 算法 是通过一系列“基本“或“简单“操作来执行计算的步骤或配方.
- “基本“操作的一种候选定义是集合 、 和
- 另一种“基本“操作的候选定义是 操作. 它可以通过多种物理方法轻松实现, 包括电子晶体管.
- 我们可以使用 计算许多其他函数, 包括多数、增量等.
- 还有其他等价选择, 包括集合 和
- 我们可以形式化定义函数 可被 NAND-CIRC 编程语言 计算的概念.
- 对于任意基本操作集合, 通过电路可计算与通过直线程序可计算的概念是等价的.
习题
习题 3.7 ( 不是通用的). 证明 不是通用门集. 见脚注中的提示. 2感谢 Nathan Brunelle 和 David Evans 对本练习的建议.
习题 3.10 (通用基底大小的界 (困难) ). 证明: 对任意集合 ( 为从 到 的函数的子集) , 如果 是通用的, 则存在一个最多 个门的 -电路来计算 函数. (可先证明存在一个大小至多 的 -电路. ) 3
习题 3.11 (电路规模与输入/输出). 证明: 对于任意具有 个输入和 个输出的 电路, 若电路规模为 则 见脚注中的提示. 4.
习题 3.13 (由激活函数构造 ). 我们称函数 为 近似器, 如果它满足以下性质: 对任意 当 且 时, 有 其中 表示与 最接近的整数. 也就是说, 当 在距离 不超过 的区域内时, 我们要求 等于与 最近的那两个 值的 值 (允许 的误差) . 若 不满足该接近条件, 则对 的值不作要求.
在本练习中你将证明可以从常见的深度神经网络激活函数构造出 近似器. 作为推论, 你将得到深度神经网络可以模拟 电路. 由于 电路也可以模拟深度神经网络, 这两种计算模型因而等价.
-
证明存在一个 近似器 其形式为 其中 为仿射函数 (即 某些 , 也是仿射函数 ( , 而 定义为 注意 其中 是常用的整流线性单元激活函数.
-
证明存在一个 近似器 其形式为 其中 如上为仿射函数, 且 定义为
-
证明存在一个 近似器 其形式为 其中 如上为仿射函数, 且 定义为
-
证明: 对任意具有 个输入且单输出的 电路 (计算函数 , 如果用 近似器替换 中的每一个门, 然后将得到的“近似电路“在某个 上求值, 则输出为某个实数 且满足
习题 3.14 (用 高效实现多数函数). 证明存在常数 使得对任意 存在一个包含至多 个门的 电路, 该电路计算 位输入的多数函数 即当且仅当 时 见脚注中的提示. 5
习题 3.15 (输出放在最后一层). 证明: 对任意 若存在一个门数为 的布尔电路 计算 则存在另一个门数不超过 的布尔电路 使得在 的最小分层 (minimal layering) 中, 输出门位于最后一层. 见脚注中的提示. 6
杂记
阿尔-花拉子米 (Al-Khwarizmi) 著作的摘录来自《The Algebra of Ben-Musa》, Fredric Rosen, 1831 年.
查尔斯·巴贝奇 (Charles Babbage, 1791-1871) 是具有远见的科学家、数学家和发明家 (参见 Swade, 2002 Collier, MacLachlan, 2000) .
在现代电子计算机发明的一个多世纪之前, 巴贝奇就意识到计算原则上可以机械化.
他设计的第一台机械计算机是 差分机 (difference engine), 用于多项式插值.
随后他设计了 解析机 (analytical engine), 这是一台更加通用的机器, 也是第一台可编程通用计算机的原型.
遗憾的是, 巴贝奇从未完成这些原型机的设计.
最早意识到解析机潜力及其深远影响的人之一是阿达·洛芙莱斯 (Ada Lovelace) (参见 第七章 注释) .
布尔代数最早由布尔 (Boole) 和德摩根 (DeMorgan) 在 1840 年代研究 Boole, 1847 De Morgan, 1847.
布尔电路的定义及其与电继电器电路的联系由香农 (Shannon) 在其硕士论文中提出 Shannon, 1938.
(霍华德·加德纳称香农的论文为“可能是 20 世纪最重要、也最著名的硕士论文“. )
萨维奇 (Savage) 的书 Savage, 1998 与本书类似, 从布尔电路作为第一个模型开始引入计算理论.
Jukna 的书 Jukna, 2012 提供了现代深入的布尔电路论述, 另见 Wegener, 1987.
Sheffer Sheffer, 1913 证明了 函数是通用的, 尽管早期 Peirce 的工作中也出现过类似结论, 参见 Burks, 1978.
怀特海德 (Whitehead) 和罗素 (Russell) 在其巨著《数学原理》 (Principia Mathematica) 中使用 作为逻辑基础 Whitehead, Russell, 1912.
Ernst 在其博士论文中 Ernst, 2009 实证研究了各种函数的最小 电路.
Nisan 和 Shocken 的书 Nisan, Schocken, 2005 从 门开始构建计算系统, 直到高级程序和游戏 (“ 到 Tetris”) ; 另见网站 nandtotetris.org.
我们在 定义 3.3 中将布尔电路的大小定义为其包含的门的数量. 这是文献中使用的两种约定之一. 另一种约定是将大小定义为导线的数量 (等价于门的数量加输入数量) .
在几乎所有情况下, 这差异很小, 但可能影响某些“病态例子“的电路规模复杂度, 例如常量零函数, 其输出几乎不依赖输入.
1: 也可以将这些函数定义为接受长度为零的输入, 这对模型的计算能力没有影响.
2: 提示: 利用 证明任何仅由 与 门构成的电路所计算的函数 都满足
3: 感谢 Alec Sun 和 Simon Fischer 对本题的评论.
4: 提示: 利用布尔电路定义中对于输入顶点必须至少有一个出边以及电路恰有 个输出门的条件. 另见相关备注 3.2
5: 提示: 一个可行的方法是使用递归并用所谓的“主定理 (Master Theorem) “进行分析.
6: 提示: 层次中位于输出之后的顶点可以安全地移除而不改变电路功能.
** 本章仍在翻译中 **
4. 语法糖与通用函数计算
学习目标
- 习惯于语法糖或高级逻辑到低级门电路的自动转换.
- 学习重要结论的证明: 任何有限函数都能通过布尔电路计算.
- 开始从量化角度思考计算过程所需的代码行数.
我们目前所考察的计算模型, 可谓极其精简.
例如. 我们的 NAND-CIRC “编程语言” 仅包含单一操作 foo = NAND(bar,blah).
本章将揭示, 这些简单模型实际上与更复杂的模型完全等价.
关键发现在于: 我们可以用基础构件来实现复杂功能, 再将这些新功能作为构件去实现更高级的功能.
这在编程语言设计领域被称为“语法糖“——因为我们并未改变底层编程模型本身, 而只是通过语法转换, 将使用了新特性的程序转译为不依赖这些特性的等效程序.
本章将提供一个“工具箱“, 以用于证明许多函数都能通过NAND-CIRC程序(进而也能通过布尔电路)进行计算. 我们还将借助这个工具箱证明一个基本定理: 任意有限函数 都能由布尔电路实现(详见下文定理 4.7).
虽然语法糖工具箱本身具有重要意义, 但定理 4.7也可以在不使用该工具箱的情况下直接证明. 我们将在第4.5节呈现这种替代证明方法. 图图 4.1概括了本章的核心结论脉络.
阅读本章, 我们希望读者能够有以下收获:
- 本章中, 我们将会得出第一个主要结果: 每个 有限函数都可以被一些布尔电路计算(参见定理 4.7 和 重要提示 4.2). 其有时也被称为 与 函数的“通用性“ (利用第3章中的等价, 这也是的“通用性“)
- 尽管定理 4.7是一项重要结论, 但其证明过程实际上并不复杂. 第4.5节将给出该结论的一个相对简洁的直接证明.
不过在第4.1节和第4.3节中, 我们采用了“语法糖“(参见重要提示 4.1)这一概念来推导该结论. 对于编程语言的理论与实践而言, 这都是一个至关重要的概念.
“语法糖“的核心思想在于: 我们可以通过基础组件实现高级功能, 从而扩展编程语言的表现力. 例如, 基于第3章介绍的AON-CIRC和NAND-CIRC编程语言, 我们可以通过扩展实现用户自定义函数(如
def Foo(...))、条件语句(如if blah ...)等高级特性. 一旦掌握了这些扩展功能, 我们就不难证明: 通过获取任意函数的真值表(即所有输入输出对应表), 可以据此创建出能将每个输入映射至对应输出的AON-CIRC或NAND-CIRC程序. - 本章中我们还将首次接触 定量分析 的概念. 虽然定理 4.7定理指出每个函数都能通过某个电路实现, 但该电路所需逻辑门的数量可能呈指数级增长. (此处使用的“指数级“并非口语中泛指的“非常巨大“, 而是精确的数学概念——当然这个数学概念恰好也意味着规模极其庞大. ) 我们发现, 某些函数 (例如, 整数加法和乘法) 事实上可以用更少的门电路计算. 我们将在第5章与接下来的章节中更加深入探讨这种“门电路复杂度“.
4.1 语法糖的一些例子
现在我们将展示若干“语法糖“转换的实例, 这些转换可用于构建直线式程序或电路. 我们主要从计算模型的直线式编程语言视角出发, 并具体以NAND-CIRC编程语言为例进行说明(以便更清晰地阐述概念). 这种视角的便利之处在于, 我们介绍的多数语法糖转换最容易理解的方式, 就是将其视为对程序源代码进行“查找替换“操作. 根据定理 3.5定理, 我们得到的所有结论同样适用于电路模型——无论是使用NAND门的电路, 还是使用AND、OR及NOT门构成的布尔电路. 虽然详细列举这类语法糖转换的实例可能略显枯燥, 但我们之所以这样做, 主要基于两个原因:
-
这可以让你确信, 尽管布尔电路或NAND-CIRC编程语言等简单模型看似基础且存在局限性, 但它们实际上具有强大的表达能力.
-
于是你就可以意识到, 选择学习计算理论课程而非编译原理课程是多么幸运…
:)
4.1.1 用户定义过程
几乎所有编程语言都具备一个核心功能: 定义并执行过程或子程序的能力(在某些语言中常称为 函数 , 但为避免与程序计算的函数混淆, 我们更倾向于使用过程这一名称). NAND-CIRC编程语言本身并未内置这种机制, 但我们可以通过沿用已久的“复制粘贴“技巧实现相同效果. 具体来说, 我们可以将定义过程的代码:
def Proc(a,b):
proc_code
return c
some_code
f = Proc(d,e)
some_more_code
替换为以下形式, 其中直接“粘贴“Proc过程的代码:
some_code
proc_code'
some_more_code
其中proc_code'是通过将Proc代码中所有a替换为d、b替换为e、c替换为f而得到的. 在执行此操作时, 我们需要确保proc_code'中出现的所有其他变量不会与其他变量产生冲突——这总是可以通过将变量重命名为之前未使用过的新名称来实现.
由上述推理, 我们可以得到以下定理:
NAND-CIRC-PROC只允许 无递归 过程. 事实上, 过程Proc的代码无法调用Proc, 而只能使用在其之前定义的过程.
如果没有这样的限制, 上述的“搜索并替换“的过程可能永远无法结束, 而定理 4.1随之不成立.
定理 4.1 可通过上述转换方法证明, 但由于形式化证明过程较为冗长繁琐, 此处予以省略.
样例 4.1 (使用语法糖通过NAND计算多数函数). 过程机制让我们能够更清晰简洁地表达NAND-CIRC程序. 例如, 由于我们可以通过NAND实现AND、OR和NOT运算, 因此可以通过以下方式计算 多数 函数:
def NOT(a):
return NAND(a,a)
def AND(a,b):
temp = NAND(a,b)
return NOT(temp)
def OR(a,b):
temp1 = NOT(a)
temp2 = NOT(b)
return NAND(temp1,temp2)
def MAJ(a,b,c):
and1 = AND(a,b)
and2 = AND(a,c)
and3 = AND(b,c)
or1 = OR(and1,and2)
return OR(or1,and3)
print(MAJ(0,1,1))
# 1
图 4.2 展示了通过“展开“此程序(将其中的过程调用替换为具体定义)后得到的“无糖“版NAND-CIRC程序及其对应电路.
图 4.2. 通过展开多数函数程序(样例 4.1)中的过程定义后得到的标准(即“无糖“)NAND-CIRC程序, 右侧为其对应电路. 需注意, 这并非实现多数函数最高效的NAND电路/程序: 通过简化某些步骤(例如当门电路 计算 后, 门电路 又计算 的情况, 图中绿色虚线箭头标示处), 我们可以减少逻辑门的使用数量.
尽管我们可以通过使用语法糖来以一种更易读的方式 表示 NAND-CIRC程序, 我们并没有改变语言本身的定义. 因此, 不管什么时候, 当我们说某个函数 有一个 行的NAND-CIRC程序时, 我们指的总是一个标准“无糖“NAND-CIRC程序, 其中所有的语法糖都已经被展开了. 例如, 样例 4.1的程序是计算 的一个 行程序, 尽管使用NAND-CIRC-PROC时其可以用更少的代码行数写出.
4.1.2 由Python证明 (选读)
我们可以编写一个Python程序来实现定理 4.1的证明. 该程序将接受包含过程定义的NAND-CIRC-PROC程序 通过简单的“查找替换“操作将其转换为标准的(即“无糖“)NAND-CIRC程序 使得在不使用任何过程的情况下计算与相同的函数.
核心思路很简单: 如果程序包含一个带有两个参数x和y的过程Proc的定义, 那么每当遇到形如foo = Proc(bar,blah)的语句时, 我们可以用以下内容替换该行:
-
过程
Proc的主体代码(将所有出现的x和y分别替换为bar和blah) -
一行
foo = exp, 其中exp是过程Proc定义中return语句后面的表达式
为使转换更加健壮, 我们可以为Proc使用的内部变量添加前缀, 以确保它们不会与中的变量冲突; 为简化起见, 我们在下面的代码中暂不考虑这个问题, 但实际实现时可以轻松添加此功能.
以下Python函数desugar的代码实现了这样的转换:
样例 4.2 (将NAND-CIRC-PROC程序转化为标准无糖NAND-CIRC程序的Python代码).
def desugar(code, func_name, func_args,func_body):
"""
将所有具有形式
foo = func_name(func_args)
用以下代码替换
func_body[x->a,y->b]
foo = [result returned in func_body]
"""
# 使用Python的正则表达式来简化代码
# 参见 https://docs.python.org/3/library/re.html 和本书第九章
# 捕获由逗号分割的参数列表的正则表达式
arglist = ",".join([r"([a-zA-Z0-9\_\[\]]+)" for i in range(len(func_args))])
# 捕获具有下列形式的正在表达式
# "variable = func_name(arguments)"
regexp = fr'([a-zA-Z0-9\_\[\]]+)\s*=\s*{func_name}\({arglist}\)\s*$'#$
while True:
m = re.search(regexp, code, re.MULTILINE)
if not m: break
newcode = func_body
# 将函数的参数用函数调用时传入的变量替换
for i in range(len(func_args)):
newcode = newcode.replace(func_args[i], m.group(i+2))
# 将新代码插入
newcode = newcode.replace('return', m.group(1) + " = ")
code = code[:m.start()] + newcode + code[m.end()+1:]
return code
图 4.2 展示了, 对样例 4.1中使用语法糖计算的多数函数程序, 将desugar函数应用于其上得到的结果.
具体来说, 我们首先应用desugar移除OR函数的使用, 然后再次应用以移除AND函数的使用, 最后第三次应用以移除NOT函数的使用.
样例 4.2中的desugar函数假定过程定义已被拆分为名称、参数和主体部分.
虽然精确描述如何扫描定义, 并将其拆分为这些组件, 对我们的目的并不关键. 但如果感兴趣, 可以通过以下Python代码实现这一拆分过程:
def parse_func(code):
"""将一个函数定义解析为名称, 参数列表与函数体"""
lines = [l.strip() for l in code.split('\n')]
regexp = r'def\s+([a-zA-Z\_0-9]+)\(([\sa-zA-Z0-9\_,]+)\)\s*:\s*'
m = re.match(regexp,lines[0])
return m.group(1), m.group(2).split(','), '\n'.join(lines[1:])
4.1.3 条件语句
NAND-CIRC语言中另一个严重缺失的特性是条件语句(例如许多编程语言中常见的if/then结构).
不过, 通过运用过程机制, 我们可以实现一种替代的条件判断结构.
首先我们需要计算函数 该函数满足: 当 时输出 当 时输出
如习题 4.2所示, 函数可以通过NAND门按如下方式实现:
def IF(cond,a,b):
notcond = NAND(cond,cond)
temp = NAND(b,notcond)
temp1 = NAND(a,cond)
return NAND(temp,temp1)
又被称为 多路 函数, 因为可以被视作一个控制输出与还是相连的开关. 只要我们由计算函数的过程, 就可以在NAND中实现条件语句. 其思路为将具有以下形式的代码
if (condition): assign blah to variable foo
替换为具有以下形式的代码
foo = IF(condition, blah, foo)
其在condition等于时将foo赋值为旧值, 否则将foo赋值为blah的值.
更一般地, 我们将如下形式的代码
if (cond):
a = ...
b = ...
c = ...
替换为如下形式的代码
temp_a = ...
temp_b = ...
temp_c = ...
a = IF(cond,temp_a,a)
b = IF(cond,temp_b,b)
c = IF(cond,temp_c,c)
通过运用此类转换方法, 我们可以证明以下定理. 尽管其完整形式化证明(启发性有限)在此从略, 但读者可参阅第4.1.2节获取相关证明思路的提示.
4.2 拓展样例: 加法与乘法(选读)
使用“语法糖“, 我们能够写出以下的整数加法函数:
# 将两个n为整数相加
# 为了简便, 使用最低有效位优先表示法
def ADD(A,B):
Result = [0]*(n+1)
Carry = [0]*(n+1)
Carry[0] = zero(A[0])
for i in range(n):
Result[i] = XOR(Carry[i],XOR(A[i],B[i]))
Carry[i+1] = MAJ(Carry[i],A[i],B[i])
Result[n] = Carry[n]
return Result
ADD([1,1,1,0,0],[1,0,0,0,0]);;
# [0, 0, 0, 1, 0, 0]
其中zero是常数零函数, MAJ和XOR分别对应多数函数与异或函数. 虽然我们为方便起见使用了Python语法, 但此例中是某个 固定整数 , 因此对每个这样的而言, ADD都是一个接收位输入并输出位的有限函数. 特别地, 对于每个 我们只需将代码重复次(将i的值依次替换为即可消除for i in range(n)循环结构. 通过展开所有特性, 对每个的取值, 我们都能将上述程序转换为标准的(无糖)NAND-CIRC程序. 图 4.3展示了时的转换结果.
图 4.3. 通过“展开“所有语法糖功能得到的用于两个二进制数相加的NAND-CIRC程序及对应NAND电路. 该程序/电路包含43行代码/逻辑门, 但这远非最优实现. 实际上只需使用个NAND门即可完成位二进制数的加法运算, 具体实现方法参见习题 4.5.
通过仔细分析上述程序并统计逻辑门数量, 我们可以证明以下定理(另见图 4.4):
定理 4.3 (使用NAND-CIRC程序实现加法运算). 对于任意 令为如下函数: 给定 计算和所表示数值之和的二进制表示. 则存在常数 使得对每个 都存在一个最多包含行代码的NAND-CIRC程序可计算 1
只要有了加法, 我们就可以使用小学乘法算法来获得乘法, 从而得到以下定义:
我们在此省略证明过程, 不过在习题 4.7中, 我们将要求您以(用您熟悉的编程语言编写的)程序形式提供一份“构造性证明“: 该程序以数字作为输入, 输出一个最多包含行代码的NAND-CIRC程序, 用于计算函数. 实际上, 利用Karatsuba算法可以证明: 存在一个包含行代码的NAND-CIRC程序能够计算函数(若采用更优算法, 还能实现更进一步的渐进性优化).
4.3 LOOKUP函数
函数将在本章及后续章节中扮演重要角色. 其定义如下:
对于 LOOKUP 函数的图示参见 图 4.5. 事实证明, 对于每个 我们可以使用 NAND-CIRC 程序计算
定理 4.5 的一个直接推论是, 对于每个 可以由一个布尔电路(使用 AND,OR 和 NOT 门)计算, 其门数最多为
4.3.1 为构造一个NAND-CIRC程序
我们通过归纳法证明定理 4.5.
对于情况 将 映射到 换句话说, 如果 则它输出 否则它输出 (在变量重新排序后)这与 第4.1.3节 中提出的 函数相同, 该函数可以用一个4行 NAND-CIRC 程序计算.
作为一般情况的热身, 让我们考虑 的情况. 给定 的输入 和索引 如果索引的最高有效位 是 那么 将等于 如果 并等于 如果 类似地, 如果最高有效位 是 那么 将等于 如果 并将等于 如果 另一种说法是, 我们可以将 写成如下形式:
def LOOKUP2(X[0],X[1],X[2],X[3],i[0],i[1]):
if i[0]==1:
return LOOKUP1(X[2],X[3],i[1])
else:
return LOOKUP1(X[0],X[1],i[1])
换言之
def LOOKUP2(X[0],X[1],X[2],X[3],i[0],i[1]):
a = LOOKUP1(X[2],X[3],i[1])
b = LOOKUP1(X[0],X[1],i[1])
return IF( i[0],a,b)
更一般地, 如以下引理所示, 我们可以使用两次 调用和一次 调用来计算
对引理 4.1的证明
对引理 4.1的证明
如果 的最高有效位 为零, 那么索引 在 中, 因此我们可以在 的“前半部分“执行查找, 并且 的结果将与 相同. 另一方面, 如果这个最高有效位 等于 那么索引在 中, 在这种情况下, 的结果与 相同. 因此, 我们可以通过首先计算 和 然后输出 来计算
基于 引理 4.1 的 定理 4.5 证明. 既然我们已经证明 引理 4.1, 我们就可以完成 定理 4.5 的证明. 我们将通过对归纳证明, 存在一个最多 行的 NAND-CIRC 程序用于计算 对于 这由我们之前见过的用于 的四行程序得出. 对于 我们使用以下伪代码来计算:
a = LOOKUP_(k-1)(X[0],...,X[2^(k-1)-1],i[1],...,i[k-1])
b = LOOKUP_(k-1)(X[2^(k-1)],...,X[2^(k-1)],i[1],...,i[k-1])
return IF(i[0],b,a)
如果我们令 表示 所需的行数, 那么上述伪代码表明
由归纳假设, 我们有 这正是我们想要证明的.
对于我们实现的 的实际行数图, 参见 图 4.6.
4.4 通用 函数计算
此时, 关于 NAND-CIRC 程序(以及等价的布尔电路和其他等效模型), 我们知道以下事实:
- 它们至少可以计算一些非平凡函数.
- 为各种函数想出 NAND-CIRC 程序是一项非常繁琐的任务.
因此, 如果读者并不特别期待一长串可以由 NAND-CIRC 程序计算的函数示例, 这也是无可指摘的. 然而, 事实证明我们并不需要这样做, 因为我们可以一举证明 NAND-CIRC 程序可以计算 每一个 有限函数:
根据 定理 3.5, NAND 电路, NAND-CIRC 程序, AON-CIRC 程序和布尔电路的模型都是彼此等价的, 因此 定理 4.6 对所有这些模型都成立. 特别地, 以下定理等价于 定理 4.6:
改进上界 尽管对我们不是特别重要, 但仍有可能改进定理 4.6的证明, 将其削弱倍, 同时优化常数 从而证明对每个 和足够大的 若 则能被一个最多有个门电路的NAND电路计算. 该结果的证明超出了本书的范畴, 但我们确实会讨论如何得到具有形式的上界. 参见第4.4.2节和杂记
4.4.1 NAND通用性的证明
为了证明 定理 4.6, 我们需要为 每一个 可能的函数给出一个 NAND 电路, 或等价的 NAND-CIRC 程序.
我们将注意力限制在布尔函数的情况 (即
习题 4.9 要求你扩展证明, 使其对 的所有值成立.
一个函数 可以通过一个表来指定, 该表列出了它对每个 输入的值.
例如, 下表描述了一个特定的函数 2
| 输入 ( | 输出 ( |
|---|---|
| 1 | |
| 1 | |
| 0 | |
| 0 | |
| 1 | |
| 0 | |
| 0 | |
| 1 | |
| 0 | |
| 0 | |
| 0 | |
| 0 | |
| 1 | |
| 1 | |
| 1 | |
| 1 |
表格: 函数 的一个示例.
对每个 而下列则是使用LOOKUP_4过程语法糖来计算的NAND-CIRC “伪代码”.
G0000 = 1
G1000 = 1
G0100 = 0
...
G0111 = 1
G1111 = 1
Y[0] = LOOKUP_4(G0000,G1000,...,G1111,
X[0],X[1],X[2],X[3])
我们可以通过添加三行代码来定义初始化为 和 的变量 zero 和 one, 从而将这些伪代码转换为实际的 NAND-CIRC 程序, 然后将诸如 Gxxx = 0 的语句替换为 Gxxx = NAND(one,one), 并将诸如 Gxxx = 1 的语句替换为 Gxxx = NAND(zero,zero). 对 LOOKUP_4 的调用将被替换为计算 的 NAND-CIRC 程序, 并插入相应的输入.
上述推理中没有任何部分是特定于上述函数 的. 对于 每一个 函数 我们都可以编写一个 NAND-CIRC 程序来执行以下操作:
- 初始化 个变量, 从
F00...0到F11...1, 使得对于每个 与 对应的变量被赋值为 - 在上一步初始化的 个变量上计算 索引变量是输入变量
X[],…,X[]. 也就是说, 就像上面G的伪代码一样, 我们使用Y[0] = LOOKUP(F00..00,...,F11..1,X[0],..,X[])
所得程序的总行数用于初始化变量的 行代码, 加上我们为计算 所使用的 行. 这就完成了 定理 4.6 的证明.
备注 4.4 (对结果的观察). 虽然 定理 4.6 起初看起来令人惊讶, 但回想起来, 每个有限函数都可以用 NAND-CIRC 程序计算可能并不那么令人吃惊. 毕竟, 一个有限函数 可以通过简单地列出其每个 输入值的输出值来表示. 因此, 我们可以编写一个类似大小的 NAND-CIRC 程序来计算它, 这是合理的. 更有趣的是, 一些 函数, 比如加法和乘法, 具有更高效的表示: 只需要 或更少的行.
4.4.2 改进因子 (选读)
通过更加仔细的处理, 我们可以改进 定理 4.6 的上界, 并证明每个函数 都可以由一个最多 行的 NAND-CIRC 程序计算. 换句话说, 我们可以证明以下改进版本:
定理 4.8 (NAND 电路的普遍性, 改进上界). 存在一个常数 使得对于每个 和函数 都有一个最多 行的 NAND-CIRC 程序计算函数 3
对定理 4.8的证明
对定理 4.8的证明
和之前一样, 证明 的情况就足够了. 因此, 我们令 我们的目标是证明存在一个 行的 NAND-CIRC 程序(或等价地, 一个 门的布尔电路)来计算
我们令 (这个选择背后的原因稍后会变得清晰). 我们定义函数 如下:
换句话说, 如果我们使用通常的二进制表示将数字 等同于字符串 那么对于每个 和 有
(4.2) 意味着对于每个 如果我们写成 其中 和 那么我们可以通过首先计算长度为 的字符串 然后计算 来检索 中对应于 位置的元素(参见 图 4.8). 计算 的成本是 行/门, 而计算 的 NAND-CIRC 行(或布尔门)成本最多为 其中 是计算 所需的操作数(即 NAND-CIRC 程序的行数或电路中的逻辑门数).
为了完成证明, 我们需要给出 的一个界. 由于 是一个将 映射到 的函数, 我们也可以将其视为 个函数 的集合, 其中对于每个 和 有 (即 是 的第 位.) 一个不成熟的想法是, 我们可以使用 定理 4.6 以 行计算每个 但总行数为 这并没有什么优化. 然而, 关键是观察到只有 个不同的函数将 映射到 例如, 如果 与 是相同的函数, 那意味着如果我们已经计算了 那么我们可以仅用常数次操作计算 只需复制相同的值! 一般来说, 如果你有一个包含 个函数 的集合, 每个函数将 映射到 其中最多有 个不同的函数, 那么对于每个值 我们可以使用最多 次操作计算所有 个值 (参见 图 4.7).
在我们的情况下, 由于最多有 个不同的函数将 映射到 我们可以使用最多
次操作计算函数 (因此通过 (4.2) 计算出
现在剩下的就是将我们选择的 代入 (4.4). 根据定义, 这意味着 (4.4) 可以被限制在某个上界内
这正是我们想要证明的. (我们在上面使用了对于足够大的 有 的事实.)
利用 NAND-CIRC 程序与布尔电路之间的联系, 定理 4.8 的一个直接推论是以下对 定理 4.7 的改进:
4.5 通用 函数计算: 一个替代的证明
定理 4.7 是计算理论(和实践!)中的一个基本结果. 在本节中,我们将提出布尔电路可以计算每个有限函数这一基本事实的另一种证明. 这种替代证明在门数量上给出了稍差一些的定量界限, 但它的优点是更简单, 直接使用电路并避免了所有语法糖机制的使用. (然而,该机制本身是有用的,并将在以后找到其他应用.)
对定理 4.10的证明思路
对定理 4.10的证明思路
证明思路如 图 4.9 所示. 如前所述, 关注 的情况(函数 有单个输出)就足够了, 因为我们可以通过组合 个电路(每个计算函数 的不同输出位)来扩展到 的情况. 我们首先证明, 对于每个 存在一个大小为 的电路来计算函数 定义如下: 当且仅当 (即 对除了以外的所有输入, 其输出为 然后,我们可以将任何函数 写为最多 个函数 的 OR,其中 满足
对定理 4.10的证明
对定理 4.10的证明
我们针对 的情况证明这个定理. 结果可以像之前一样扩展到 的情况(另见 习题 4.9). 令 我们将通过以下步骤证明存在一个 大小的布尔电路来计算
-
我们证明对于每个 存在一个 大小的电路来计算函数 其中 当且仅当
-
然后我们证明这说明了存在一个 大小的电路来计算 通过将 写为所有使得 的 的 的 OR. (如果 是恒零函数, 因此没有这样的 那么我们可以使用电路 )
我们从步骤 1 开始:
断言: 对于 定义 如下:
那么存在一个使用最多 个门的布尔电路来计算
断言证明: 证明如 图 4.10 所示. 例如, 考虑函数 这个函数在 上输出 当且仅当 且 因此我们可以写 这转化为一个有一个 NOT 门和两个 AND 门的布尔电路. 更一般地, 对于每个 我们可以将 表示为 其中如果 我们将 替换为 如果 我们将 替换为简单的
这产生一个使用 个 AND 门和最多 个 NOT 门来计算 的电路, 因此总共最多需要 个门. 现在对于每个函数 我们可以写出
其中 是 输出 的输入集合.
(要观察到这一点, 你可以验证 (4.5) 的右边在 上求值为 当且仅当 在集合 中.) 因此, 我们可以使用最多 个门的布尔电路来计算每个 个函数 并结合最多 个 OR 门, 从而获得一个最多 个门的电路. 由于 其大小 最多为 因此这个电路中门的总数是
4.6 类
我们已经看到, 每个 函数 都可以由一个大小为 的电路计算, 并且 一些 函数(如加法和乘法)可以由更小的电路计算.
我们定义 为映射 位到 位的函数的集合, 这些函数可以由最多 个门的 NAND 电路计算(或者等价地, 由最多 行的 NAND-CIRC 程序计算). 形式化地, 其定义如下:
图 4.11 描绘了集合 注意 是 函数 的集合, 而不是 程序 的集合! 就像 图 4.12 所示的那样, 询问一个程序或电路是否是 的成员是一种 类别错误!
正如我们在3.7.2节(和第2.6.1节)中讨论的, 程序 和 函数 之间的区别是绝对关键的. 你应该始终记住, 虽然一个程序能 计算 一个函数, 但它并不 等于 一个函数. 特别是, 如我们所见, 可以有多个程序计算同一个函数.
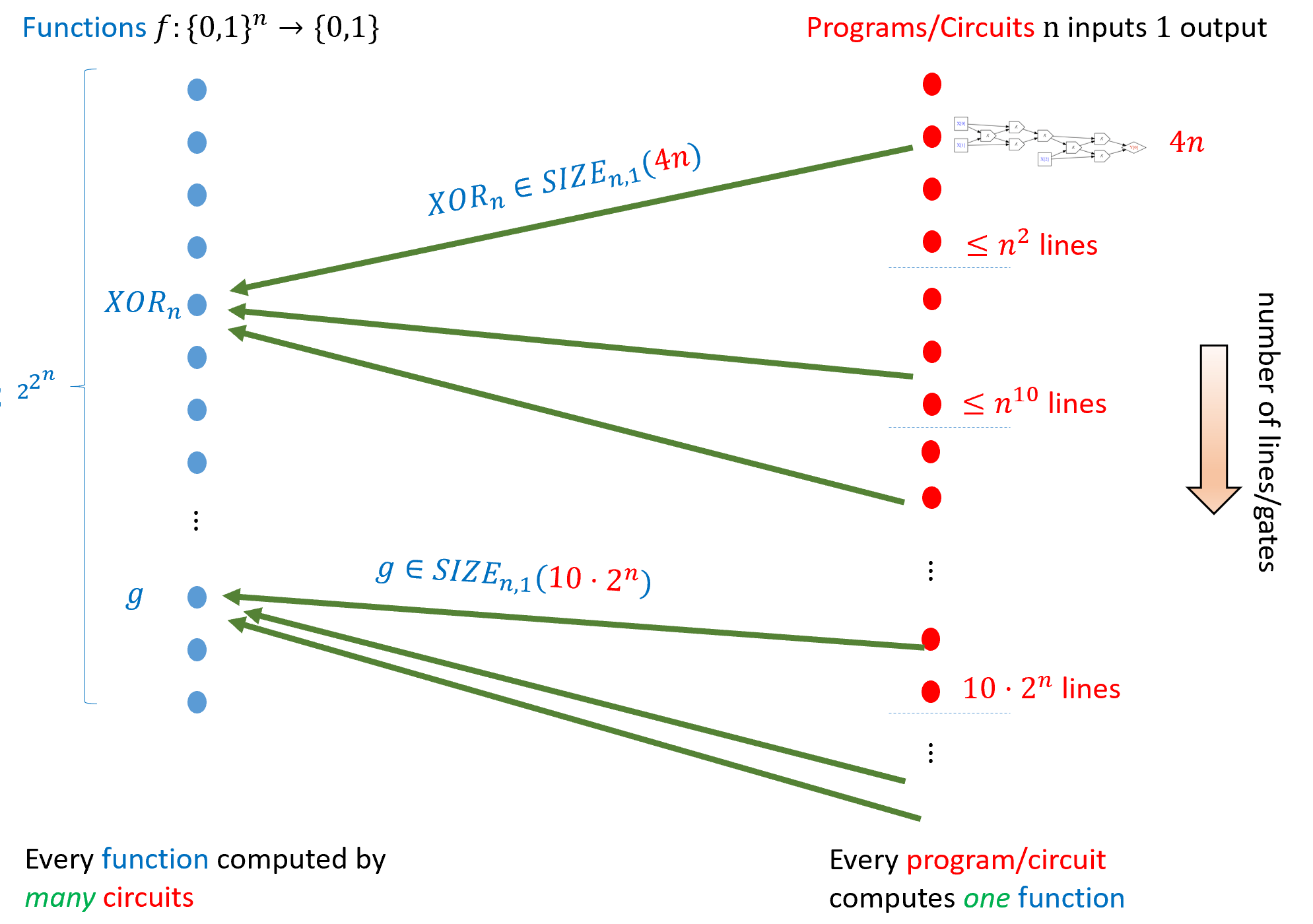
图 4.11. 有 个函数映射 到 以及无限多个具有 位输入和单比特输出的电路. 每个电路计算一个函数, 但每个函数可以由许多电路计算. 如果计算 的最小电路有 个或更少的门, 我们说 例如 定理 4.6 表明_每个_函数 都可以由某个最多 个门的电路计算, 因此 对应于从 到 的 所有 函数的集合.
虽然我们针对NAND门定义了 但如果我们针对AND/OR/NOT门定义它, 我们基本上会得到相同的类:
对引理 4.2的证明
对引理 4.2的证明
如果 可以由最多 个门的NAND电路计算, 那么通过用NOT和AND两个门替换每个NAND门, 我们可以获得一个最多 个门的AND/OR/NOT布尔电路来计算 另一方面, 如果 可以由最多 个门的布尔AND/OR/NOT电路计算, 那么根据 定理 3.3 , 它可以由最多 个门的NAND电路计算.
我们在本章中所见到的结果可以被表述为证明 与 定理 4.6 说明对于某个常数 等于从 到 的所有函数的集合.
备注 4.5 (有限与无限函数). 与诸如 Python 、C 或 JavaScript 等编程语言不同, NAND-CIRC 和 AON-CIRC 编程语言中没有 数组. 一个 NAND-CIRC 程序 有固定数量的输入和输出变量 和 因此, 例如, 没有单个 NAND-CIRC 程序可以计算增量函数 该函数将字符串 (我们通过二进制表示将其视为数字)映射到表示 的字符串. 相反, 对于每个 存在一个 NAND-CIRC 程序 它计算函数 限制到长度为 的输入 由于可以证明对于每个 这样的程序 存在且长度最多为 因此对于每个
目前, 我们的重心将放在 有限 函数上, 但我们将在后面的 第13.6节 中讨论如何将大小复杂度的定义扩展到具有无界输入长度的函数.
对练习 4.1的解答
对练习 4.1的解答
如果 那么存在一个 行 NAND-CIRC 程序 计算
我们可以将 中的变量 Y[0] 重命名为 temp, 并在最后添加一行
Y[0] = NAND(temp,temp)
来获得一个计算 的程序
- 我们可以通过一个简化的“编程语言“来定义计算函数的概念, 其中在 步内计算函数 对应于拥有一个 行的 NAND-CIRC 程序来计算
- 虽然 NAND-CIRC 编程只有一种操作, 但其他操作如函数和条件执行可以使用它来实现.
- 每个函数 都可以由一个最多 个门的电路计算(实际上最多 个门).
- 我们有时(或者总是?)可以将计算 的 高效 算法翻译成一个电路, 该电路计算 的门数量与算法中的步数相当.
4.7 习题
习题 4.4 (条件语句).
在这个练习中, 我们将探索 定理 4.2 : 将使用诸如 if .. then .. else .. 代码的 NAND-CIRC-IF 程序转换为标准的 NAND-CIRC 程序.
习题 4.8 (高效乘法 (挑战)). 使用你最喜欢的编程语言编写一个程序,该程序在输入整数 时,输出一个计算 的 NAND-CIRC 程序,并且最多有 行.6 你能用多少行来相乘两个 2048 位数字?
习题 4.10 (使用语法糖简化). 设 为以下 NAND-CIRC 程序:
Temp[0] = NAND(X[0],X[0])
Temp[1] = NAND(X[1],X[1])
Temp[2] = NAND(Temp[0],Temp[1])
Temp[3] = NAND(X[2],X[2])
Temp[4] = NAND(X[3],X[3])
Temp[5] = NAND(Temp[3],Temp[4])
Temp[6] = NAND(Temp[2],Temp[2])
Temp[7] = NAND(Temp[5],Temp[5])
Y[0] = NAND(Temp[6],Temp[7])
-
编写一个程序 最多三行代码,使用
NAND以及语法糖OR,计算与 相同的函数. -
绘制一个电路,计算与 相同的函数,并仅使用 和 门.
在以下练习中,要求你比较每对编程语言的 表达能力. 当我们说 “比较” 两个编程语言 和 的 “表达能力” 时, 我们指的是确定分别使用 和 中的程序可计算的函数集之间的关系. 也就是说, 要回答该问题, 你需要同时完成以下两项:
- 要么 证明对于 中的每个程序 都有 中的一个程序 计算与 相同的函数, 要么 给出一个函数示例,该函数可由 -程序计算但不可由 -程序计算.
和
- 要么证明对于 中的每个程序 都有 中的一个程序 计算与 相同的函数, 要么 给出一个函数示例,该函数可由 -程序计算但不可由 -程序计算.
当你给出上述示例,即一个函数在一种编程语言中可计算但在另一种中不可计算时,你需要 证明 你展示的函数 (1) 在第一种编程语言中可计算,并且 (2) 在第二种编程语言中 不可计算.
习题 4.12 (比较 XOR 和 NAND).
设 XOR-CIRC 为编程语言,其中有以下操作 foo = XOR(bar,blah), foo = 1 和 bar = 0 (即,我们可以使用常量 和函数 它将 映射到 比较 NAND-CIRC 编程语言和 XOR-CIRC 编程语言的表达能力.参见脚注中的提示.7
习题 4.13 (多数函数的电路). 证明存在某个常数 使得对于每个 其中 是 个输入比特上的多数函数.即 当且仅当 参见脚注中的提示.8
4.8 杂记
关于电路的更广泛讨论, 请参阅 Jukna 和 Wegener 的著作 Jukna, 2012, Wegener, 1987. Shannon 证明了每个布尔函数都可以由指数级大小的电路计算 Shannon, 1938. 改进的 界(对于许多基, 是最优值)归功于 Lupanov Lupanov, 1958. 关于 NAND 情况(其中 的阐述可以在他的著作 Lupanov, 1984 的第 4 章中找到. (感谢 Sasha Golovnev 追踪到这个参考文献!)
“语法糖“的概念也称为“宏“或“元编程”, 有时通过编程语言或文本编辑器中的预处理器或宏语言实现. 一个现代例子是 Babel JavaScript 语法转换器, 它将使用最新特性编写的 JavaScript 程序转换为旧版浏览器可以接受的格式. 它甚至有一个 插件 架构, 允许用户将自己的语法糖添加到语言中.
2: 如果你好奇的话, 该函数的作用是, 在输入 (我们将其解释为 中的一个数字) 时, 输出 在二进制下的第 位.
3: 这个定理中的常数 最多为 并且实际上可以任意接近 参见杂记.
4: 你可以先从将 转换为使用过程语句的 NAND-CIRC-PROC 程序开始, 然后使用 样例 4.2 的代码将后者转换为“无糖“的 NAND-CIRC 程序.
5: 使用一个逐位相加的“级联“, 从最低有效位开始, 就像小学算法一样.
6: 提示: 使用 Karatsuba 算法.
7: 你可以使用以下事实: 特别地,这意味着如果你有行 d = XOR(a,b) 和 e = XOR(d,c),那么 e 得到变量 a, b 和 c 在模 意义下的和.
- 数据即代码, 代码即数据
数据即代码, 代码即数据
学习目标
- 理解计算中的最重要概念之一: 代码与数据的二元性.
- 逐步熟悉程序的不同表示形式之间的转换.
- 学习构建一个“通用电路求值器”, 能够根据给定表示执行其他电路.
- 认识与上一章结论相辅相成的重要成果: 某些函数需要 指数级 数量的门电路才能实现.
- 探讨 在物理意义上的Church-Turing论题 –该论题指出布尔电路可以建模物理世界中 所有 可行的计算, 并分析其背后的物理学原理与哲学意涵.
“密码脚本”这一术语显然过于狭隘. 染色体结构同时是实现它们所预示的发展的工具——它们既是法律条文又是执行权力, 或者用另一个比喻来说, 它们同时是建筑师的设计图和施工者的技艺.
——埃尔温·薛定谔(Erwin Schrödinger), 1944年
“数学家几乎不会将64种四个单元的三联体组合与二十种其他单元之间的对应关系称为‘普适’, 而这种对应很可能是地球生命最根本的普遍特征. “
——米沙·格罗莫夫(Misha Gromov), 2013年
程序就是由一系列符号组成的序列, 每个符号都可以通过(例如)ASCII标准编码为由和组成的字符串. 因此, 我们可以将每个NAND-CIRC程序(进而每个布尔电路)表示为二进制字符串. 这个论断看似浅显, 实则意义深远–它意味着我们既可以将电路或NAND-CIRC程序视为执行计算的指令, 也可以将其视为可能被其他计算用作 输入 的 数据 .
这种 代码 与 数据 的对应关系是计算科学最根本的特性之一. 它构成了 通用 计算机概念的基础(使计算机不需要预先布线即可执行不同任务), 也为实现 通用 人工智能的愿景提供了理论支撑. 这一理念从脚本语言到机器学习等计算领域都有广泛应用, 但客观而言, 人类尚未完全掌握其精髓. 许多安全漏洞(如图 5.1所示的“缓冲溢出”案例)正是由于攻击者成功在系统仅预期接收“被动”数据的位置注入了可执行的代码. 代码与数据的关联性甚至超越了电子计算机的范畴: 例如DNA即可被视为程序也可被视为数据(正如薛定谔在DNA发现前出版的著作所言–这部著作后来启发了沃森与克里克–DNA同时承载着“建筑师的设计图”与“施工者的工艺”).
阅读本章, 我们希望读者能够有以下收获:
-
本章将初步探讨代码与数据对应关系的多种应用.
-
我们将首先通过将程序/电路表示为字符串的方式, 统计 特定规模内的程序/电路数量, 并借此获得与第4章结论相对应的成果——第四章我们证明了所有函数都可以通过电路计算, 但该电路可能具有指数级规模(具体界限见定理 4.7). 本章将证明 某些 函数确实无法突破这个限制: 计算这些函数的 最小 电路必然具有指数级规模.
-
我们还将利用程序/电路字符串化表示的概念, 证明“通用电路“的存在性——即能够对其他电路求值的电路. 在编程语言领域, 这被称为“自循环解释器“: 用某编程语言编写的能评估同语言其他程序的程序. 这些结论存在重要限制: 通用电路的规模必须大于其评估的电路. 我们将在第7章引入 循环 和 图灵机 时展示如何突破这一限制.
-
本章成果概览参见图 5.2.
5.1 将程序表示为字符串
我们可以用无数种方式将程序或电路表示为字符串. 例如, 由于布尔电路是带标签的有向无环图, 我们可以使用邻接矩阵或邻接表来表示它们. 然而, 由于程序代码本质上只是字母和符号的序列, 可以说程序在概念上最简单的表示就是这样的序列. 例如, 以下NAND-CIRC程序
temp_0 = NAND(X[0],X[1])
temp_1 = NAND(X[0],temp_0)
temp_2 = NAND(X[1],temp_0)
Y[0] = NAND(temp_1,temp_2)
本质上是一个包含107个符号的字符串, 这些符号包括大小写字母、数字、下划线_、等号=、标点符号(如“(”、“)”、“,”)、空格以及“换行”标记(通常表示为“\n”或“↵”). 每个这样的符号都可以通过ASCII编码用7位二进制字符串表示, 因此程序可以被编码为一个长度为位的字符串.
上述讨论中没有任何内容是特定于程序的, 因此我们可以用相同的推理证明 每个 NAND-CIRC程序都可以表示为中的字符串. 实际上, 我们可以做得更好. 由于NAND-CIRC程序的工作变量名称不会影响其功能, 我们总是可以将程序转换为的形式, 其中除输入和输出之外的所有变量都具有temp_0、temp_1、temp_2等形式. 此外, 如果程序有行, 我们永远不需要使用大于的索引(因为每行最多涉及三个变量), 同样地, 输入和输出变量的索引也都不会超过 由于0到之间的数字最多可以用位数字表示, 程序中的每一行(形式为foo = NAND(bar,blah))可以用个符号表示, 每个符号又可以用7位表示. 因此, 一个行程序可以表示为位组成的字符串, 由此得到以下定理:
我们省略了定理 5.1的正式证明, 但请确保你理解为什么它可以从上述推理中得出.
5.2 程序数量统计与NAND-CIRC程序规模下界
将程序表示为字符串的必然结果是: 特点长度的程序数量受限于可表示它们的字符串数量. 这一结论对我们4.6节定义的集合具有重要意义.
对定理 5.2的证明
对定理 5.2的证明
对于任意 我们将构造一个从到长度为的字符串集合的单射映射(其中为常数). 这将完成证明, 因为该证明表明小于长度至多为的所有字符串集合的规模. 根据等比数列求和公式, 后一个集合的规模为
映射将简单地把函数映射到计算的最小程序表示. 由于 根据定理 5.1, 存在一个最多行的程序 其字符串表示长度不超过 此外, 映射是单射, 因为对于任意不同的函数 必然存在某个输入为使得 这意味着分别计算和的程序不可能完全相同.
定理 5.2有一个重要推论: 可用小型电路/程序计算的函数数量远少于函数总数, 因此必然存在需要非常大规模(实际上是 指数级规模 )电路才能计算的函数. 理解这一点需要注意: 映射到可由其在输入上的四个值唯一确定;映射到的函数可尤其在输入上的八个值唯一确定. 更一般地, 每个函数都可等同于其在上个取值组成的列表. 因此, 映射到的函数数量等于可能存在的长度取值列表的数量, 即 注意这是关于的双重指数函数, 因此即使对于较小的值(比如 从到的函数数量也是真正的天文数字. 2如前所述, 这引出了如下推论:
存在常数 使得对于所有足够大的 必然存在函数满足 也就是说, 计算的最短NAND-CIRC程序需要超过行. 3
对定理 5.3的证明
对定理 5.3的证明
证明相当简单. 令为满足的常数, 且设 则当时, 有: 这里利用了时以及的事实. 由于小于从比特映射到1比特的函数总数, 必然存在至少一个函数不属于 这正是我们需要证明的结论.
我们此前已经知道: 每个 从映射到的函数都可由行程序计算. 定理 5.3表明了该界限是紧的, 因为某些函数确实需要如此天文数字的行数才能计算.
事实上, 正如习题中所探讨的, 大多数函数都属于这种情况. 因此, 能用少量代码行数计算的功能(如加法、乘法、图上的最短路径算法, 甚至函数)只是例外而非普遍规律.
5.2.1 规模层次定理(可选)
由定理 4.8有包含了所有由到的函数, 而由定理 5.3, 存在一些没有包含在中的函数 换而言之, 对于充分大的 有
可以发现我们可以使用定理 5.3来展示一个更加一般的结论: 当我们增加我们门电路的“预算”的时候, 我们就能计算新的函数.
对定理 5.4的证明思路
对定理 5.4的证明思路
为了证明这个定理, 我们需要找到一个函数 使得该函数 可以 由个门的电路计算, 但不能被个门的电路计算. 为此, 我们将构筑一个函数序列 其满足以下性质: (1) 最多 可以 用个门的电路计算; (2) 无法 用个门的电路计算;(3) 对每个 若可用规模为的电路计算, 则最多可用规模为的电路计算. 这些性质共同表明: 若令是满足的最小下标, 则由于 必然有 这正是我们需要证明的结论. 示意图见图 5.4.
对定理 5.4的证明
对定理 5.4的证明
设是由定理 5.3保证存在的函数, 且满足 我们定义函数序列如下: 对任意 若是在字典序中的编号, 则 函数是常值零函数, 而等于 此外, 对每个 函数与最多在一个输入上存在差异(即满足的输入
设 并令是满足的最小下标. 由于 这样的下标必然存在, 且因常值零函数属于 故
根据的选取, 属于 为完成证明, 需要证明 令是满足的字符串, 为的值. 则也可定义为 即 其中 是将 映射到(若两者相等)或(否则)的函数. 由的选取可知, 最多可用个门计算, 且易证 因此最多可用个门计算, 命题得证.
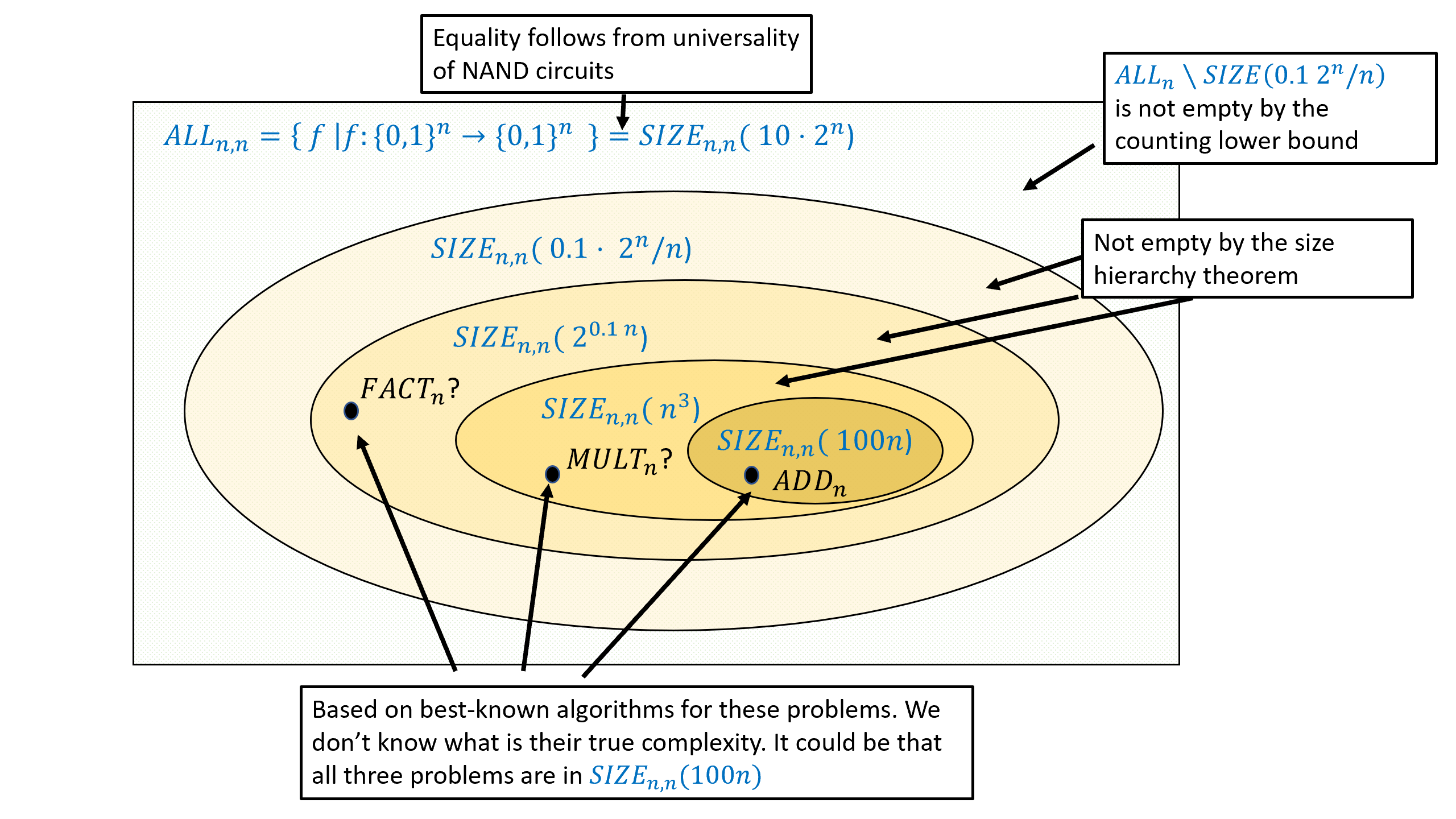
图 5.5. 关于规模复杂度类已知结论的示意图(未按比例绘制). 该图描绘了形如的类, 但其他规模复杂度类(如的情况类似. 由定理4.12(结合4.4.2节的改进)可知: 所有比特到比特的函数都可由规模为(的电路计算; 另一方面, 计数下界(定理 5.3, 另见习题 5.4)表明某些函数需要个门; 规模分层定理(定理 5.4)则证明当时必然存在属于的函数, 另见习题 5.5.
我们还考虑了一些具体示例: 两个比特数的加法可在线路中完成, 而两个比特数的乘法目前尚无此类程序, 但已知可在甚至更优规模内完成. 上图中的对应乘法的逆问题——求给定整数的质因数分解. 目前尚未发现任何具有多项式(甚至次指数)级别线路数量的电路能计算
5.3 元组表示
ASCII码能很好地呈现程序, 但对某些应用场景而言, 采用更具体的NAND-CIRC程序表示方法更为实用. 本节将介绍一种便于后续使用的特定表示方案.
NAND-CIRC程序本质上是由若干行如下形式的语句构成的序列:
blah = NAND(baz,boo)
变量命名本身并不具有特殊性. 尽管可读性会降低, 但我们完全可以仅使用temp_0、temp_1等工作变量来编写所有程序. 因此, 我们的NAND-CIRC程序表示法将忽略变量实际名称, 转而采用为每个变量分配编号的方案. 我们将程序中的每一 行 编码为数字三元组. 若某行形式为foo = NAND(bar,blah), 则将其编码为三元组 其中对应变量foo的编号, 和分别对应bar和blah的编号.
具体而言, 我们将为每个变量分配集合中的唯一编号. 前个数字对应输入变量, 最后个数字对应输出变量, 中间数字则对应剩余的“工作区“变量. 形式化定义如下:
元组列表表示法是我们在表示NAND-CIRC程序时默认采用的方案. 鉴于“元组列表表示法“这个名称略显冗长, 我们通常直接称其为程序的“表示法“. 当输入数量和输出数量可通过上下文明确时, 我们有时会直接用列表而非三元组来表示程序.
将NAND-CIRC程序从代码表示转换为元组列表表示是一项直观的编程任务, 仅需几行Python代码即可实现4. 虽然元组列表表示法会丢失变量命名等信息, 但这并不影响程序功能, 因此完全可接受.
5.3.1 从元组到字符串
如果程序的规模为 则其变量数量最多为(因为每行代码最多涉及三个变量). 因此我们可以通过补前导零的方式, 将每个在范围内的变量索引编码为长度为的字符串. 由于这是定长编码, 自然满足无前缀性, 因此我们可以将个三元组组成的列表(对应程序的行编码)简单地表示为所有编码连接而成的长度为的字符串.
我们定义为表示规模程序对应列表的字符串长度. 由上述推导可得:
我们可以通过将和的无前缀表示作为前缀附加到列表之前, 从而将表示为字符串. 由于(程序必须至少涉及其所有输入和输出变量各一次), 这些无前缀表示可以用长度为的字符串进行编码. 特别地, 每个最多包含行代码的程序都可以用长度为的字符串表示. 类似地, 每个最多包含个逻辑门的电路也可用长度为的字符串表示(例如通过将转换为等效程序实现).
5.4 使用NAND-CIRC实现的NAND-CIRC程序解释器
既然程序可以表示为字符串, 我们亦可将程序本身作为一个函数的输入. 更具体地, 对于每个自然数我们定义函数如下: 其中已在(5.1)中定义, 同时, 我们使用在5.1节中介绍的具体表示方案.
换而言之, 接受两个字符串的拼接作为输入: 字符串和字符串 若是表示三元组列表的字符串, 且是某个规模为的NAND-CIRC程序的元组列表表示, 则等于程序在输入的求值结果 否则, 等于(这种情况并不重要, 只是表示错误的“垃圾值”).
核心要点: 定义的具体细节并不重要, 但以下要点需要记忆:
- 是一个有限函数, 接受固定长度的字符串作为输入, 并输出固定长度的字符串.
- 是单一函数, 计算该函数可对任意固定长度的NAND-CIRC的程序在对应长度下的任意输入进行求值.
- 是一个函数, 而非程序(回忆3.7.2节中的讨论). 即是描述输入与输出对应关系的规范. 是否存在计算 的程序(即该函数的实现)是一个独立问题, 需要另行证明(我们将在定理 5.5中实现, 并在定理 5.6中给出更高效的程序).
本书中我们将首次遇到的自我循环的示例是以下定理, 可将其理解为“用NAND-CIRC实现的NAND-CIRC解释器”:
也就是说, NAND-CIRC程序能够接受任何其他NAND-CIRC程序(需满足特定长度和输入/输出要求)的描述以及任意输入 并计算程序在输入下的结果. 根据NAND-CIRC程序与布尔电路的等价性, 我们也可以将视为一个接受其他电路描述及其输入, 并返回其求值结果的电路(参见图 5.6). 我们将这个计算 、的NAND-CIRC程序称为有界通用程序(或通用电路, 参见图 5.6). “通用”意味着这是一个可以执行任意代码的单一程序, 而“有界”表示仅能评估有限规模的程序. 当然这种限制是NAND-CIRC编程语言固有的, 因为一个行的程序(或等效的个门的电路)最多只能接受个输入. 后续在第7章中, 我们将引入循环的概念(以及图灵机模型), 从而突破这一限制.
对定理 5.5的证明
对定理 5.5的证明
5.4.1 高效通用程序
定理 5.5虽然确立了存在计算函数的NAND-CIRC程序, 但并未明确限定该程序规模的边界. 我们用于证明定理4.9的定理 5.5仅能保证存在一个规模可能达到输入长度指数级的NAND-CIRC程序. 这意味着即使对于中等规模的参数(例如 计算所需的NAND程序行数甚至可能超过可观测宇宙中的原子数量! 幸运的是, 我们能够实现比这好得多的方案. 事实上, 对于任意 都存在一个输入长度为多项式级规模的NAND-CIRC程序可计算 如下述定理所示:
与定理 5.5不同, 定理 5.6并非“任意有限函数均可用电路计算”这一事实的平凡推论. 证明定理 5.6需要构造一个具体的NAND-CIRC程序来计算函数, 我们将通过以下阶段实现:
- 首先用“伪代码”描述计算的算法流程;
- 随后展示如何用Python编写实现该函数的程序(无需深入掌握Python知识, 任何具备编程语言基础的读者都能理解);
- 最终演示如何将此Python程序转化为NAND-CIRC程序.
这种方法不仅证明了定理 5.6, 更揭示了重要规律: 我们总是可以将Python等高级语言的(无循环)代码转化为NAND-CIRC程序(进而转化为布尔电路).
5.4.2 “伪代码”形式的NAND-CIRC解释器
要证明定理 5.6, 只需给出一个具有行代码的NAND-CIRC程序, 该程序能够计算包含行代码的NAND-CIRC程序. 首先思考: 若不受限于仅执行NAND操作, 我们应如何计算此类程序? 换而言之, 我们将非正式地描述一个算法: 当输入、三元组列表以及字符串时, 该算法能计算由表示的程序在输入上的输出.
接下来我们将描述这样的算法. 假设我们拥有一个位数组数据结构, 可为每个存储位 具体而言, 若变量Table存储此数据结构, 则我们假定能执行以下操作:
GET(Table,i): 获取Table中索引i对应的位. 其中i为范围内的整数.Table = UPDATE(Table,i,b): 更新Table使其索引i对应的位变为b. 其中i为范围内的整数,b为中的位.
算法 5.1通过逐行计算输入程序, 并更新Vartable以记录每个变量的值. 在执行结束时, 它输出索引位置对应的变量(这些变量对应程序的输出变量).
5.4.3 Python实现的NAND解释器
为了使内容更加具体, 我们来看如何在Python语言中实现算法 5.1. (选择Python并无特殊意义, 我们同样可以轻松地使用JavaScript、C、OCaml或其他任何编程语言实现相应函数. )我们将构建一个函数NANDEVAL, 该函数在输入时, 会输出由所表示的程序在上的求值结果. 为简化说明, 我们暂不考虑不能表示具有个输入和个输出的有效程序的情况. 具体代码展示于图 5.7中.
def NANDEVAL(n,m,L,X):
# 执行一个由元组列表表示的NAND-CIRC程序
s = len(L) # 行数
t = max(max(a,b,c) for (a,b,c) in L)+1 # L + 1中的最大编号
Vartable = [0] * t # 初始化变量表
# 辅助函数
def GET(V,i): return V[i]
def UPDATE(V,i,b):
V[i]=b
return V
# 加载输入值到变量表
for i in range(n):
Vartable = UPDATE(Vartable,i,X[i])
# 执行程序
for (i,j,k) in L:
a = GET(Vartable,j)
b = GET(Vartable,k)
c = NAND(a,b)
Vartable = UPDATE(Vartable,i,c)
# 返回输出 Vartable[t-m], Vartable[t-m+1],....,Vartable[t-1]
return [GET(Vartable,t-m+j) for j in range(m)]
# 在XOR上测试(2个输入, 1个输出)
L = ((2, 0, 1), (3, 0, 2), (4, 1, 2), (5, 3, 4))
print(NANDEVAL(2,1,L,(0,1))) # XOR(0,1)
# [1]
print(NANDEVAL(2,1,L,(1,1))) # XOR(1,1)
# [0]
访问数组Vartable中特定索引处的元素仅需常数次基本操作. 因此(由于且 上述程序将执行量级的基本操作. 5
5.4.4 用NAND-CIRC构建NAND-CRIC解释器
现在我们来阐述定理 5.6的证明. 要证明该定理, 仅提供一个Python程序是不够的. 我们需要展示如何通过NAND-CIRC程序计算函数 换言之, 我们的任务是为每一组 将5.4.3节中的Python代码转换为能计算函数的NAND-CIRC程序
在继续阅读之前, 请思考你将如何给出{{ref:thm:eff-bounded-univ}的“构造性证明”. 也就是说, 思考如何用你选择的编程语言编写函数universal(s,n,m), 使其在输入时输出能计算的NAND-CIRC程序的代码. 这个函数与前述Python程序NANDEVAL存在微妙但关键的差异: 函数universal并非实际执行给定程序对输入的求值, 而是输出一个能计算映射关系的NAND-CIRC程序代码.
我们的构造将紧密遵循前文中EVAL的Python实现. 我们将使用变量Vartable[],Vartable[](其中来存储变量. 但NAND不具备整数值变量, 因此我们不能编写类似Vartable[i]的代码(其中i为变量). 然而, 我们可以实现函数GET(Vartable,i)来输出数组变量表的第i位——这实质上正是我们在定理 4.5中见过的函数!
我们已知, 对于选择的 可以在时间内计算
对于每个 令对应长度为数组的UPDATE函数. 即对于输入 等于满足以下条件的
其中我们将字符串通过二进制表示视为中的数字. 我们可以通过行NAND-CIRC程序计算 具体如下:
综合以上两点, 我们可以通过以下方式计算UPDATE函数(使用有限循环的语法糖):
def UPDATE_ell(V,i,b):
# 输入: V[0]...V[2^ell-1], i ∈ {0,1}^ell, b ∈ {0,1}
# 输出: NewV[0],...,NewV[2^ell-1]
# 更新后的数组满足NewV[i]=b, 其余位置与V相同
for j in range(2**ell): # j = 0,1,2,...,2^ell -1
a = EQUALS_j(i)
NewV[j] = IF(a,b,V[j])
return NewV
由于UPDATE函数中的循环j会运行次, 且计算需要行代码, 因此计算UPDATE的总行数为 一旦我们能计算GET和UPDATE函数, 剩余的实现主要是需要仔细处理的“簿记工作”, 但这并不需要深度的理解, 因此我们省略完整细节. 由于我们运行GET和UPDATE函数次, 计算的总行数为 至此(除省略的细节外), 我们完成了定理 5.6的证明.
上述NAND-CIRC程序比其Python版本效率低, 因为NAND不支持能够进行高效随机访问的数组. 例如, 对位数组的查找操作在NAND中需要行代码, 而在Python中仅需步(或可能为步, 取决于计数方式).
事实上, 可以改进定理 5.6的界限, 使用行NAND-CIRC程序来求值行NAND-CIRC程序. 关键在于将NAND-CIRC程序的描述视为电路, 特别是视为有界入度的有向无环图(DAG). 用于行程序的通用NAND-CIRC程序将对应于此类顶点DAG的通用图 我们可以将此类图视为通信网络的固定“布线”, 它应能适应个顶点之间任意可能的通信模式(该模式对应一个行NAND-CIRC程序). 事实证明, 存在高效的路由网络, 允许将任何顶点电路嵌入到大小为的通用图中, 更多内容请参阅第5.9节.
5.5 用NAND-CIRC实现Python解释器(讨论)
为了证明定理 5.6, 我们实际上将Python程序EVAL的每一行代码都转换为了等价的NAND-CIRC代码片段. 不过, 我们的推理过程并不特定于这个具体函数. 实际上, 我们可以将每一个Python程序都转换为具有可比效率的等价NAND-CIRC程序. (更具体地说, 如果Python程序在长度不超过的输入上执行次操作, 那么存在一个行数的NAND-CIRC程序, 能在长度为的输入上与Python程序产生相同输出. )虽然具体实现需要处理大量细节并超出本书范围, 但请允许我说明为何你应该相信这在原理上是可行的.
首先, 我们可以使用CPython(Python的参考实现), 通过C程序来执行任意Python程序. 再结合C编译器, 就能将Python程序转换为多种“机器语言“. 因此, 要将Python程序转化为等价的NAND-CIRC程序, 只需证明如何将机器语言程序转换为等价的NAND-CIRC程序. ARM架构就是一类极简(因此相当便利)的机器语言, 它驱动着包括几乎所有安卓设备在内的移动设备. 6还存在更简单的机器语言, 例如为LLVM编译器用于实现后端的LEG架构(因此可以编译该编译器支持的大量且不断增长的语言列表中的任何语言). 其他例子包括受交互式证明系统(我们将在第22章介绍它们)启发的TinyRAM架构, 以及面向教学的超级简易计算机架构. 逐一处理这些计算机的指令集并将其转换为NAND片段虽枯燥但可行. 实际上, 这最终与将高级代码转换为实际硅门电路的过程非常相似, 而硅门操作与NAND-CIRC程序的操作并无太大差异. 事实上, 像MyHDL这样实现“从Python到硅芯片转换”的工具, 就可以用于将Python程序转换为NAND-CIRC程序.
NAND-CIRC编程语言仅是一种教学工具, 我绝对没有表示编写NAND-CIRC程序或编译器是一种实用、有用或令人愉悦的活动. 但我希望你理解为何这能够实现, 并确保在紧要关头(至少为了你的成绩), 你有信心完成这项任务. 理解Python等高级语言程序如何最终转换为NAND这样的具体底层表示, 是计算机科学的基础.
敏锐的读者可能注意到, 上述段落仅说明了为何可能为每个特定Python可计算函数找到具有可比效率的特定NAND-CIRC程序来计算 但这似乎与我们编写“用NAND实现的Python解释器”的目标仍有距离——这意味着对于每个参数 我们需要给出一个单一的NAND-CIRC程序 使得在给定Python程序的描述、特定输入以及操作步数上限(其中和的长度以及的值均不超过时), 该程序能返回在上最多执行步的结果. 毕竟, 上述转换将每个Python程序转化为不同的NAND-CIRC程序, 并未产生能够评估所有Python程序的“万能NAND-CIRC程序”. 然而, 我们实际上可以获得一个能执行任意Python程序的单一NAND-CIRC程序. 原因在于存在用Python编写的Python解释器: 即一个能读取比特串、将其解释为Python代码并执行的Python程序 因此, 我们只需要展示一个能计算与特定Python程序相同功能的NAND-CIRC程序 就能获得执行所有Python程序的方法.
我们反复看到的是计算的通用性或自引用概念, 即所有足够丰富的计算模型都足以“模拟自身”. 这种现象对计算理论和实践(以及远超出该领域的范畴, 包括数学基础和科学基本问题)的重要性, 无论如何强调都不为过.
5.6 物理扩展Church-Turing论题(讨论)
我们已经看到, NAND门(和其他布尔运算)在物理世界中可以通过截然不同的系统实现. 那么其反方向呢? 即NAND-CIRC程序能否模拟任何物理计算机?
我们可以踏出大胆的一步并规定: 布尔电路(或其等价的NAND-CIRC程序)确实囊括了我们能想到的所有计算. 这个关于无限函数的陈述(我们将在第7章中遇到)通常归功于Alonzo Church和Alan Turing, 故我们将其称为Church-Turing论题. 正如我们将在后续课程中讨论的, Church-Turing论题并非数学定理或猜想, 而是像物理学理论一样, 是对现实世界的数学建模. 在有限函数的语境下, 我们可以提出如下非正式的猜想或预测:
如果一个函数在物理世界中可以用单位的“物理资源”计算, 那么它也能通过大致个门的布尔电路程序计算.
先验地看, 假设我们简陋的NAND-CIRC程序或布尔电路模型能捕获所有可能的物理计算可能显得极端. 但一个多世纪以来, 在计算技术的发展中, 尚未有人构建出任何可扩展的计算设备来挑战这一假设.
现在我们更详细地讨论PECTT的“细则”, 以及迄今为止针对它提出的(未成功的)挑战. 对于“大致物理资源”这一表述并无普遍认同的形式化定义, 但我们可以通过考虑物理计算设备的尺寸和计算输出所需的时间来近似这一概念, 并要求任何此类设备都能被布尔电路模拟, 其门数量是系统尺寸和运行时间的多项式(指数不太大).
换句话说, 我们可以将PECTT表述为: 任何可由占用空间体积、耗时完成计算的设备计算的函数, 必须也能由门数为的布尔函数电路计算, 其中是关于和的多项式.
函数的具体形式并未达成普遍共识, 但广泛接受的是, 如果是一个指数级困难的函数(即其NAND-CIRC程序行数不少于 那么展示一个能在现实世界中计算中等输入长度(如的的物理设备, 将违反PECTT.
我们可以尝试更精确地将PECTT表述如下: 假设有一个物理系统 接受个二进制刺激并产生二进制输出, 且可被容纳于体积为的球体内. 我们说系统在秒内计算函数 是指当我们将刺激设置为某个值时, 如果在秒后测量输出, 会得到
那么, PECTT 可以表述为: 如果存在这样的系统在秒内计算 则存在一个计算的NAND-CIRC程序, 其行数最多为 其中是某个归一化常数. (我们也可以考虑使用表面积而非体积, 或将的幂次改为 2 以外的值, 但这些选择不会对以下讨论产生定性影响. )特别地, 假设是一个函数, 任何NAND-CIRC程序都需要至少行(通过定理 5.3可知这样的函数存在). 那么PECTT意味着, 计算的系统要么体积至少为 要么时间至少为 由于这个量随呈指数级增长, 不难设置参数使得即使对于中等大小的 这样的系统也无法存在于我们的宇宙中.
为了使PECTT完全具体化, 我们需要确定测量时间和体积的单位以及归一化常数 一种保守的选择是假设我们可以将计算压缩到绝对物理极限(这远远超出当前技术的多个数量级), 这对应于设并使用普朗克单位表示体积和时间. 普朗克长度(粗略地说, 是理论上可测量的最短距离)约为米. 普朗克时间(光传播一个普朗克长度所需的时间)约为秒. 在上述设置中, 如果一个函数接受1KB的输入(例如, 约位, 可编码一张的位图), 且需要至少行NAND程序计算, 那么任何计算它的物理系统要么需要普朗克长度立方的体积(超过立方米), 要么需要至少普朗克时间单位(超过秒). 为了感知这个数字有多大, 请注意宇宙年龄仅约秒, 其可观测半径仅约米. 以上讨论表明, 通过展示一个小于宇宙尺寸的系统来计算此类函数, 可以在经验上证伪PECTT.
当然, 以这种方式反驳PECTT存在几个障碍, 其中之一是我们无法在所有可能的输入上测试系统. 然而, 事实证明我们可以利用交互式证明和程序检查等概念(可能在本书后续遇到)绕过这个问题. 另一个更显著的问题是, 虽然我们知道许多困难函数存在, 但目前没有单个显式的函数 我们能证明其NAND-CIRC程序所需行数的下界为(更不用说
5.6.1 反驳PECTT的尝试
人类令人钦佩的特质之一, 就是拒绝接受局限. 这种特质最美好的体现, 是人们完成了历史上长期被认为“不可能”的挑战——例如实现重于空气的(物体的)飞行、将人类送上月球、完成环球航行, 甚至是证明费马大定理. 而最糟糕的体现, 则是人们不断重蹈失败覆辙, 执意尝试那些已被证明不可能的任务, 例如制造永动机、用尺规三等分角或驳斥贝尔不等式. PECTT(及其多种形式)同时吸引了这两类人. 以下是一些曾被推测能够完成常规NAND-CIRC程序无法实现的计算任务的物理设备:
- 意大利面排序: 计算机科学学生最早接触的下界定理之一, 是对个数进行排序需要次比较. 而“意大利面排序”则描述了一种试图突破这一限制的“机械计算机”: 若要排序个数字 可将根意大利面切割为对应长度, 然后握成一束竖直置于平面——面条下端自然会形成有序排列. 但这种设计存在诸多缺陷, 无法真正挑战PECTT, 笔者在此保留悬念, 让读者自行发现其中奥妙.
- 肥皂泡: 欧几里得Steiner树问题被认为需要大量NAND门电路才能解决. 该问题要求判断给定平面上的个点(坐标范围为到的整数, 可用长度的字符串表示)能否通过总长度不超过的线段连接. 这个被推测为NP完全问题(后续课程将涉及该概念)的函数, 其计算复杂度很可能随增长呈指数级增长——根据PECTT, 当达到一定规模(如数百量级)时, 任何物理设备都无法计算该函数. 然而有人声称, 只需木钉和肥皂就能构造出解决该问题的简易物理设备: 将个木钉固定在两点玻璃板之间的对应坐标点, 形成的肥皂膜会以最小化总能量的方式连接所有木钉(总能量与线段总长度相关). 但该设备的缺陷在于: 自然与人一样容易陷入“局部最优解“——最终配置往往无法达到全局能量最小值, 而是停留在局部最优状态. Aaronson通过实际实验(见图 5.8)发现, 虽然该设备对三四个木钉有效, 但随着数量增加, 计算结果就会逐渐偏离最优解.

图 5.8. Scott Aaronson正在测试使用肥皂泡来计算Steiner树的一种候选设备
- DNA计算: 有人提出利用DNA的特性来解决复杂的计算问题. DNA的主要优势在于能在极小的物理空间内编码大量信息, 并以高度并行的方式处理这些信息. 截至本文撰写时, 已有实验证明, 在半径约1毫米的区域内可用DNA存储约比特信息, 而最先进的硬盘技术仅能存储约比特. 虽然这对PECTT尚未构成实质性质疑, 但提示我们应谨慎设定常数项的选择, 且不应假定当前硬盘+硅基技术已是物理极限. 7
- 连续/实数计算机: 物理世界常使用时空间等连续量进行描述, 因而有观点认为模拟设备可能直接处理实数计算, 其本质能力应超越NAND机等离散模型. 关于物理世界本质是连续还是离散的争论仍是未解之谜——事实上, 我们甚至无法精确表述该问题, 更遑论解答. 但无论如何, 测量连续量所需付出的代价显然会随精度要求而增长, 因此这类机器无法提供“免费午餐”或规避PECTT的途径(另见这篇论文). 与此相关的还有“超计算”或“芝诺计算机”提案: 通过第一秒完成第一步操作、半秒完成第二步、四分之一秒完成第三步等方式试图利用时间连续性. 这些尝试失败的原因与保证阿基里斯最终追上乌龟的芝诺悖论解决方案类似.
- 相对论计算机与时间旅行: 前文论述基于经典时间观, 但根据相对论, 时间具有观测者依赖性. 解决难题的一种思路是让计算机从自身参照系经历长时间运行, 而确保从我们视角看仅经过片刻. 实现方式可以是用户启动计算机后, 以近光速短途慢跑再返回查看结果. 根据速度差异, 用户的几秒钟可能相当于计算机时代的数个世纪(甚至足够完成Windows系统更新! ). 当然关键在于: 用户所需能量与接近光速的程度成正比. 更有趣的提案是利用闭合类时曲线(CTCs)进行时间旅行——通过保存当前状态后回到过去继续运算, 可实现任意长计算时间. 若CTCs确实存在, 我们或许需要修正PECTT(不过到时候我大可以回到过去修改这些笔记, 声称自己从未提出该猜想…)
- 人类: 另一个被提议作为PECTT反例的计算系统是半径约0.1米、重约3磅的人脑. 人类能行走、交谈、感知以及执行NAND-CIRC程序通常无法完成的任务, 但他们是否能计算NAND-CIRC程序不可计算的部分函数? 当前确实存在人类表现优于计算机的计算任务(例如某些电子游戏), 但基于现有认知, 人类(或其他生物)并不具备超越计算机的固有计算优势. 人脑约含个神经元, 每个每秒处理约1000次运算, 因此粗略估算模拟人脑一秒活动需要约个门电路的布尔电路. 8需注意, 此类电路(可能)存在并不意味易于发现——进化构建人脑耗费了数十亿年. 当前人工智能研究多专注于发掘能复现部分脑功能的程序, 这些程序虽需要巨大计算资源来发现, 但其规模常远小于上述悲观估计. 例如截至本文撰写时, 谷歌机器翻译神经网络仅含约个节点(可由同等规模NAND-CIRC程序模拟). 自远古起, 哲学家、神职人员等便主张人类存在机械装置无法捕捉的特质; 但即便确有此可能, 目前仍然没有有力证据表明人类能完成复杂度相当的计算机本质上无法实现的计算任务. 9
- 量子计算. 对PECTT最有力的挑战来自量子计算. 该理念源于观察到强量子效应系统难以用计算机模拟, 研究者反过来提议利用此类系统完成传统计算无法实现的任务. 截至本文撰写时, 可扩展量子计算机尚未建成, 但这一迷人设想似乎与任何已知自然法则都不冲突. 我们将在第23章详细讨论: 量子计算需将布尔电路模型扩展为包含特殊门的量子电路, 但其核心启示在于——量子计算虽要求我们修正PECTT, 却无需彻底颠覆世界观. 事实上, 无论底层计算模型是布尔电路还是量子电路, 本书绝大部分内容依然成立.
尽管PECTT的精确表述及其正确性仍是活跃研究方向, 其多种变体已经在实践中被隐式地假设成立. 当前政府、企业及个人依赖密码学保护其最重要的资产, 包括国家机密、武器系统控制权、关键基础设施安全、商业保障与隐私保护. 应用密码学中常见“密码系统提供128位安全性“的表述, 其真实含义是: (a) 猜想不存在远小于规模的布尔电路(或等效NAND-CIRC程序)能破解 (b) 假定其他物理机制亦无法超越该效率, 故破解X需消耗约量级资源. 使用“猜想”而非“证明”是因为: 虽然可将“破解系统无法由门电路实现”表述为精确数学猜想, 但目前无法对任何非平凡的密码系统证明该论断. 此问题与后续章节将讨论的与问题相关, 我们将在第21章深入探讨.
- 我们可以将程序视为某个过程的描述, 也可以将其视为符号列表, 这种列表可被看作数据, 并作为其他程序的输入.
- 我们可以编写一个能计算任意NAND-CIRC程序的NAND-CIRC程序(或等效地, 一个能计算其他电路的电路). 此外, 这样做的效率损失并不大.
- 我们甚至可以编写一个能计算其他编程语言(如Python、C、Lisp、Java、Go等)程序的NAND-CIRC程序.
- 作为理论上的重大一跃, 我们可以假设计算函数的最小电路中的门数量大致反映了计算所需的物理资源量. 这一观点被称为物理扩展Church-Turing论题(PECTT).
- 布尔电路(或等效的AON-CIRC或NAND-CIRC程序)涵盖了广泛的计算模型. 目前对PECTT最有力的挑战来自利用量子力学效应加速计算的潜力, 这种模型被称为量子计算机.
5.7 第一部分的回顾: 有限计算
本章标志着本书的第一部分, 即有限计算部分的结束(即计算将固定个布尔输入映射到固定个布尔输出的函数). 第3章、第4章和第5章的主要要点如下:
- 我们可以形式化地定义函数使用个基本运算进行计算的概念. 无论这些运算是AND、OR、NOT、NAND还是其他通用基函数, 都不会产生本质差异. 这类计算既可以通过电路描述, 也可以通过直线程序描述.
- 我们定义为最多由个门电路实现的NAND电路可计算的函数集合. 该集合等同于最多由行代码实现的NAND-CIRC程序可计算的函数集(其中的常数倍差异可忽略);这也等同于最多又个AND/OR/NOT门组成的布尔电路可计算的函数集. 需要注意的是, 是一个函数集合, 而不是程序或电路的集合.
- 任意函数都可通过最多个门电路实现, 而某些函数至少需要个门电路. 我们将定义为所有最多使用个门电路可计算的、从到的函数集合.
- 我们可以将电路或程序表示为字符串. 对于任意 都存在一个通用电路或程序 它能够根据字符串描述的程序来执行长度为的程序. 这些表示方法还可以用于统计最多包含个门电路的数量, 从而证明某些函数无法通过小于指数规模的电路来计算.
- 如果存在一个由个门电路计算函数的电路, 那么我们可以使用个基本组件(如晶体管)构建物理设备来计算 PECTT假设其逆命题同样成立: 如果每个计算函数的电路至少需要个门电路, 那么任何计算的物理设备都需要消耗单位的“物理资源”. PECTT面临的主要挑战是量子计算, 我们将在第23章讨论该主题.
下章预告: 下一部分我们将探讨如何对无界输入的计算任务建模. 这些任务通过函数(或进行规范, 此类函数可接受任意数量的布尔输入.
5.8 习题
证明存在一个数 使得对于每个足够大的和每个 存在一个函数 需要至少个NAND门来计算. 提示见脚注. 10
证明存在一个数 使得对于每个和 存在一个函数 提示见脚注. 11
证明对于每个 如果足够大, 则存在一个函数 使得 提示见脚注. 13
假设 并且我们随机选择一个函数 对于每个 的值通过投掷独立的无偏硬币来确定. 证明存在一个行程序来计算的概率至多为 14
习题 5.9.
以下是一个表示NAND程序的元组:
- 按照顺序写出八个值、、、、、、、的表格.
- 用文字描述该程序的功能.
习题 5.11 (学习电路(挑战性, 可选, 需要更多背景知识)).
(本练习假设你可能此时不具备概率论和/或机器学习的背景知识. 可以在后续阶段, 特别是在学习第18章之后再来回顾. ) 在本练习中, 我们将使用对大小为的电路数量的界限来表明(如果我们忽略计算成本)每个这样的电路都可以从不太多的训练样本中学习. 具体来说, 如果我们找到一个大小为的电路, 该电路在来自某个分布的个训练样本上正确分类, 那么可以保证它在整个分布上表现良好. 由于布尔电路建模了许多物理过程(如果(有争议的)PECTT成立, 可能包括所有过程), 这表明所有这样的过程也可以被学习(再次忽略在训练数据上找到表现良好的分类器的计算成本).
设是上的任意概率分布, 是一个具有个输入、一个输出且规模为的NAND电路. 证明存在某个常数 使得以下情况以至少的概率成立: 如果且是从中独立选取的, 那么对于每个电路 如果在每个上 则
换句话说, 如果是一个所谓的“经验风险最小化器”, 在所有训练样本上与一致, 那么它也有高概率与从分布中抽取的样本上的一致(即, 使用机器学习术语来说, 它“泛化”了). 提示见脚注. 16
5.9 参考书目
函数通常被称为通用电路. 我们在本章中所描述的实现并非目前已知最高效的. Valiant(Valiant)最早提出了规模为的通用电路(其中表示输入规模). 近年来, 由于在密码学中的应用(参见Lipmaa, Mohassel, Sadeghian, 2016, Günther, Kiss, Schneider, 2017), 通用电路获得了新的研究动力.
尽管我们已经知道“大多数”将比特映射到1比特的函数需要规模为指数级的电路, 但事实上我们尚未找到任何一个显式函数能够被证明需要至少甚至规模的电路. 目前已知的最强下界表明: 存在非常简洁且显式的变量函数, 其计算至少需要线路(参见Iwama等人的论文以及Kulikov等人更近期的研究). 针对受限电路模型证明下界是一个极具吸引力的研究领域, Jukna的著作(Jukna, 2012)(另见Wegener(Wegener, 1987))为此提供了优秀的入门指南和综述. 本人从Sasha Golovnev处获悉规模分层定理(定理 5.4)的证明.
Scott Aaronson关于信息具有物理性的博客文章, 对PECTT相关议题进行了精彩探讨. 其关于NP完全问题与物理现实的综述(Aaronson, 2005)也讨论了这些议题, 不过建议在学完第15章中关于与完全性的内容后再阅读会更易理解.
1: 其中表示法中的隐常数小于10. 也就是说, 对于所有足够大的 详见备注 5.1. 如1.7节所述, 我们采用10这个界限值仅仅是因为它是个整数.
2: “天文数字”在此是一种保守表述: 可观测宇宙中的恒星数量甚至粒子数量都远少于
3: 常数至少为0.1, 实际上, 可以通过习题 5.7将其进一步缩小为任意接近的值.
4: 若想了解具体实现代码, 请参阅我们的GitHub代码库
5: Python虽不区分列表与数组, 但允许对这两种结构中的索引元素进行常数时间随机访问. 若考虑程序长度真正无界(例如超过的情况, 则访问成本将变为与数组或列表长度的对数相关, 但与的差异不影响本文后续讨论.
6: ARM代表“Advanced RISC Machine”, 而RISC又代表“Reduced instruction set computer”(精简指令集计算机).
7: 我们在PECTT的参数设定上极为保守, 甚至假设在毫米级区域内可能存储高达比特的信息.
8: 该估算可能存在数量级偏差: 一方面模拟神经胶质等其它脑组织可能导致更高开销; 另一方面, 为达成相同计算任务未必需要完全复刻大脑.
9: 亦有知名科学家主张人类具有优于计算机的固有计算能力, 参见此文.
10: 存在多少个从到的函数? 注意, 我们对电路的定义要求每个输出对应一个唯一的门, 尽管这一限制最多会对门数产生的附加差异.
11: 遵循定理 5.4证明, 将计数论证的使用替换为习题 5.4.
12: 使用邻接表表示法, 具有个入度为零的顶点和个入度为二的顶点的图可以用大约位表示. 个输入顶点和个输出顶点的标记可以通过中的个标记列表和中的个标记列表来指定.
13: 提示: 使用习题 5.6的结果, 并注意在此范围内且
14: 提示: 等价的说法是, 你需要证明使用最多行可以计算的函数集合的元素个数少于 你能看出为什么吗?
15: 注意, 如果足够大, 那么很容易用位表示这样的一对, 因为我们可以用位表示程序, 并且我们总是可以将表示填充到恰好长度.
16: 提示: 使用我们对大小为的程序/电路数量的界限定理 5.2, 以及Chernoff界(未完成引用 1)和联合界.
6. 无限域函数,自动机与正则表达式
学习目标
- 在 长度无界 的输入上定义函数,这种函数无法用一个大小有限的、由输入和输出构成的表格描述
- (前者)与语言的成员资格判定任务的等价性
- 确定性有穷自动机(可选): 一个无界计算模型的简单案例
- (前者)与正则表达式的等价性
布尔电路的模型(或者说,NAND-CIRC编程语言)有一个非常明显的短板: 一个布尔电路只能计算一个 有限的 函数 事实上,由于每个门配有两个输入,大小为的电路至多能计算长度为的输入.
因此该模型无法捕捉到这样一种直观概念: 算法可以视作对潜在的无穷函数进行的 统一处理 .
比方说,标准的小学乘法算法是一种 统一 算法,它可以对所有长度的数进行乘法运算的. 然而,这种算法无法被表达为单一的电路,而是需要对每种输入配备一个不同的电路(或者说,NAND-CIRC语言). (见图 6.1)
本章拓展了计算任务的定义,使其考虑配备 无界 定义域的函数. 其重点在于定义计算 哪些 任务,将 如何 计算的绝大部分留给之后的章节. 其中将会认识到 图灵机 与其他在无界输入上进行计算的计算模型. 然而,这一章将认识到一个简单且受限的计算模型——确定性有穷自动机(DFAs).
阅读本章, 我们希望读者能够有以下收获:
- 本章将会讨论以任意长度字符串作为输入的函数,其中主要关注 布尔 函数这种特例,其输出为单个位.
- 除此之外仍然有无数多个输入长度无界的函数. 因此这一的函数不能被任何一个单一的布尔电路计算. 这个章节的第二部分将会讨论 有穷自动机 ,这种计算模型可以计算一个输入长度无界的函数.
- 确定性有穷自动机不像Python或其他通用编程语言一样强大. 但它可以作为这些更加通用的计算模型的一个引子.
- 本章将会展示一个美妙的结果——能被有穷自动机计算的函数与能被 正则表达式 计算的函数精确地一致.
- 然而,读者仍然可以自由跳过自动机的部分,直接转向第七章中对于 图灵机 的讨论.
6.1 输入长度无界的函数
直到现在,我们考虑的计算任务都将某些长度为的字符串映射为某个长度为的字符串.
然而,一般情况下的计算任务都会涉及到长度无界的输入 例如,接下来的Python函数会计算一个函数 其中 为 当且仅当中的数量为奇数.
(换言之,对每个 , 虽然简单,却无法被一个布尔电路计算. 相反,对每个,都需要通过不同的电路计算(函数在的限制)(e.g. 见图 6.2).
def XOR(X):
'''接受一个0与1的列表X
当1的个数为奇数时输出1
否则输出0'''
result = 0
for i in range(len(X)):
result = (result + X[i]) % 2
return result
尽管能用有限多个符号来描述(事实上在上面已经做过了),它却能接受无穷多种可能的输入,因此无法把它所有的函数值都写下来. 这对其他蕴含着其他重要计算任务的函数也是同理,包括加法,乘法,排序,在图上寻找路径,由点拟合曲线,等等.
为了和有限情况作区分,有时将函数(或称为 无限的 . 然而,这不意味着可以接收一个无限长的输入. 它仅仅表明可以接收任意长的输入,因此无法简单地把在一个表上把不同输入下的全部输出都写下来.
如前所述,不失一般性的前提下,我们可以把注意力限制在输入和输出为二进制串的函数. 因为其他的对象,像数字、列表、矩阵、照片、视频、以及别的种种,都可以用二进制串编码.
如前所述,有必要区分 规范 和 实现 这两个概念 . 例如,考虑以下函数.
在数学上,这是一个良定义的函数. 对每个都会有一个非即的函数值. 然而,截至目前,尚未已知能计算该函数的Python程序. 孪生素数猜想主张对每个都有一个使得均为素数.
如果该猜想成立,那么(译者注:此处应指很容易计算—— def T(x): return 1是一个奏效的程序.
然而,自1849年起,数学家们对该猜想的证明均无功而返.
这说明,不论知不知道函数的 实现 ,上面的定义提供的都是它的 规范 .
6.1.1 改变输入和输出
许多有趣的函数都接受不止一个输入,例如函数:
接受一个二进制表示的整数对,并输出积的二进制表示. 然而,因为一对字符串能被表达为一个单一的字符串,所以像这样的函数,可以被视为从到的映射. 一般不考虑底层细节,比如把一对整数精确地表达为串的方式,因为近乎所有的选择对我们的目标而言都是等价的.
我们想计算的另一个函数是
以一个单个位作为输出. 以一个单个位为输出的函数成为 布尔函数 . 布尔函数是计算理论的中心,因此将在这本书中经常性地被讨论. 需要注意的是,即使布尔函数只有一个单一位用于输出,其输入可以是任意长度的. 因此它们仍然无法通过一个由函数值组成的有限表格描述,因此仍然是一个无限函数.
“布尔化“函数 . 有时从一个非布尔函数中构造一个布尔函数的变体是非常方便的. 例如,下列函数是的一个布尔函数变体:
如果能够通过例如Python,C,JAVA等任何一门编程语言计算,也可以计算,反之亦然.
对练习 6.1的解答
对练习 6.1的解答
对每个函数 可以定义.
其输入满足 ,而输出为的第i位(如果且
如果,则当且仅当时为,通过这一点可以计算的长度. 从出发计算是十分直接的. 另一方面,给定一个计算的Python函数,可以通过如下方法计算
def F(x):
res = []
i = 0
while BF(x,i,1):
res.append(BF(x,i,0))
i += 1
return res
6.1.2 形式语言
对每个布尔函数,可以定义集合 这样的集合被称为 语言 . 这个名字源于 形式语言理论 ,像Noam Chomsky这样的语言学家致力于该理论. . 一个 形式语言 是(更一般地说,其中是一个有限的字母表1). 一个语言上的 成员资格问题 或 判定问题 ,是断定对于给定的,是否有 如果能够计算函数,也就能够判定语言的成员资格,反之亦然. 因此,许多像Sipser,1997这样的教材都将计算一个布尔函数的任务称为“判定一个语言“ 本书主要用 函数 的记号来描述计算任务,这种方法更容易推广到不止一位输出的计算任务. 然而,因为语言的术语在文献中更加流行,有时也会提到它们.
6.1.3 函数的限制
如果是一个布尔函数而,则在输入长度为上的限制记作,是一个有限函数使得对每个均有 这就是说是定义在上的有限函数,但在这些输入上与保持一致. 因为是一个有限函数,所以它可以被一个布尔电路计算. 以下定理表明了这一点.
特别地,定理 6.1表明甚至对于前面描述过的函数,这样的电路族也存在,即使尚未已知的程序可以对其进行计算. 这实际上并不令人惊讶: 对每个特定的,要么是常0函数要么是常1函数,其中任何一者都可以用一个简单的布尔电路计算. 因为计算的电路族一定存在,用Python或其他任何编程语言计算的难度源于这样一个事实——我们不知道对每个特定的,电路族中的应该是什么.
6.2 确定性有穷自动机(可选)
我们目前所有的计算模型——布尔电路和无分支程序——都只对 有限 函数有效.
在第七章中,将会介绍 图灵机 ,这是输入长度无界函数的中心计算模型. 然而,本节将会介绍一个更加基本的模型—— 确定性有穷自动机 (DFA)
自动机可以视作通往图灵机的一个优秀的垫脚石,尽管它们在这本书的后面部分并不会大量地被用到,所以读者可以自由跳过到第七章.
DFA在能力上与 正则表达式 是等价的: 正则表达式是识别模式的一个强力工具,在实践中广泛应用. 本书对自动机的处理是相对简略的. 有大量的资源可以帮助你更加熟悉DFAs. 详细地说,第一章中Sisper的著作Sipser, 1997包含对这个内容的绝佳的说明. 这里有许多的在线自动机模拟器网站,也有将自动机和正则表达式互化的翻译器. (例如此处和此处).
从高视角上看,一个 算法 是通过以下步骤的组合从输入计算输出的方法:
- 从输入读入一位
- 更新 状态 (工作记忆)
- 停止并产生一个输出
例如,回忆以下计算函数的Python程序
def XOR(X):
'''接受一个0与1的列表X
当1的个数为奇数时输出1
否则输出0'''
result = 0
for i in range(len(X)):
result = (result + X[i]) % 2
return result
每一步中,程序读入一个位X[i]并且根据它更新自己的result状态(在X[i]为1时翻转result,否则保持原样). 当它遍历完输入后,程序输出result.
在计算机科学中,这样一个程序称为 单遍常数内存算法 ,因为它只遍历一次输入,而它的工作记忆是有限的.
(事实上,在这个案例中,result非即
这样一个算法称为 确定性有穷自动机 或 DFA (DFAs的另一个名字是 有限自动机 ).
我们可以把这样一种算法视作一个拥有个状态的“机器“,其中为常数.
这样一种机器从某个初始状态开始,然后从输入中一次读取一个位
只要这个机器读入了一个位,它就会根据和先前的状态转换到一个新的状态.
机器的输出决定于最终状态. 每个单遍常数内存算法都和这样一个机器一致.
如果这个算法使用了位内存,那么其内存中的内容就能用一个长度为的串表达. 因此对于这样一个算法的任意一个执行点,其都在至多个状态之中.
我们可以通过一个条规则的列表来指明一个拥有个状态的DFA2. 每条规则都有这样的形式: “如果DFA位于状态,读入的输入位为,则新状态为”. 在计算的最后,会有一个具有形式“如果最终状态为下列中的一者 … 则输出,否则输出“的规则. 举例而言,上述的Python程序可以用一个两个状态的自动机来计算
- 初始化为状态
- 对每个状态和读取的输入位,如果则将状态转移为,否则停留在状态
- 最终当且仅当时输出
我们也可以用一个带标号的个顶点的 图 来描述个状态的DFA. 随每个状态和位,我们添加一条带有标号的从到的有向边,使得若DFA位于状态且读入,则DFA转移到状态 (如果状态不变,则这个边是一个指向原状态的圈; 相似地,如果在和两种情况下都转移为状态,则图上会有两条平行的边)同时也会标明在最后使自动机输出的状态集 这个集合称为 接受状态 集.
图 6.3给出了XOR自动机的图形表示
形式化地讲,一个DFA由 (1) 条规则构成的表格,该表格用 转移函数 表示. 将状态和位映射到状态 DFA将会在输入下从状态转移到 和 (2) 接受状态集
确定性有穷自动机可以通过几种等价的方法定义.
特别地,Sisper在Sipser,1997将DFA定义为五元组,其中为状态集,为字母表,为转移函数,是初始状态,为接受状态集.
该书中状态集总是如下形式而初状态总是,但这对这些模型的计算能力没有影响. 因此,我们将注意力局限在字母表与相等的情况.
对练习 6.2的解答
对练习 6.2的解答
当要求构造一个DFA时,可以首先通过更加一般的、形式化的方式,来构造一个单遍常数内存算法,这通常是有效的. (例如使用伪代码或者一个python程序). 一旦得到了这样一个算法,就可以机械式地将其翻译为一个DFA. 以下是计算的一个简单Python程序:
def F(X):
'''当且仅当X是零个或多个[0,1,0]的拼接时返回1'''
if len(X) % 3 != 0:
return False
ultimate = 0
penultimate = 1
antepenultimate = 0
for idx, b in enumerate(X):
antepenultimate = penultimate
penultimate = ultimate
ultimate = b
if idx % 3 == 2 and ((antepenultimate, penultimate, ultimate) != (0,1,0)):
return False
return True
既然我们维护了三个布尔变量,工作记忆就可以是种配置中的一个,因此上述程序可以直接翻译为一个状态DFA. 尽管这对解决问题没有必要,通过检查结果DFA,会发现可以通过合并一些状态得到一个状态自动机,该自动机在图 6.4中描述. 图 6.5中描述了在一个特定输入上这个DFA的运行.
对自动机的剖析(有限vs无界)
既然我们已在考虑输入长度无界的计算任务,将算法中拥有 固定长度 的组件,和大小随输入增长的组件区分开,是非常关键的任务. 对于DFAs而言,要分类的是下列部分:
固定大小组件: 给定一个DFA ,下列量是固定的,与输入大小无关:
- 中 状态 数
- 转移函数 (有种输入,因此可以用一个行的表格描述,每一项都是中的一个数字).
- 接收状态集 该集合可以用一个中的串描述,以指明哪些状态位于中而哪些没有.
以上这些意味着,可以通过有限多个符号完全地描述一个自动机. 这是我们要求的任何一种“算法“的概念都拥有的一个共同性质: 我们应当能够写下如何从输入生成输出的完整规范.
无界大小组件: 以下关于DFA的量不以任何常数作为上界. 需要强调的是,对于任何给定的输入,它们仍然是有限的.
- 提供给DFA的输入的大小. 输入长度总是有限的,但是不能预先设定上界.
- DFA执行的步数可以随输入长度而增长. 事实上,DFA进行单次便利,因此对于一个输入,它精确地执行步.
图 6.5. 图 6.4中DFA的执行过程. 状态数和转移函数的大小是有界的,但是输入可以是任意长的. 如果DFA位于状态且读取值,则其转移到状态 在执行的最后,当且仅当最终状态位于时DFA接受该输入.
DFA可计算函数
如果有一个可以计算,就称一个函数是 DFA可计算的 . 在第四章中,我们发现每个有限函数都可以被某些布尔电路计算,因此,在此刻,你可能会希望每个函数都可以被 某些 DFA计算. 然而,有很多并 不是 这种情况. 我们马上就会发现一些简单的,却无法被DFA计算的无限函数. 但对于初学者,我们先证明这样的函数是存在的.
对定理 6.2的证明思路
对定理 6.2的证明思路
每个DFA都能用一个有限长度的串来描述,从而产生一个从到的满射: 更准确地说,这个函数将一个描述自动机的串对应到计算的函数.
对定理 6.2的证明
对定理 6.2的证明
每个DFA都能用一个表示转移函数和接收状态集的串描述,而每个DFA 都计算 某些 函数 因此可以定义如下函数 其中是对于所有输入,其均输出的常函数(也是中的一个函数). 因此根据定义,每个中的函数都可以被 某些 自动机计算,而是从到的满射,这就意味着可数. (见节 2.4.2)
因为 所有 布尔函数的集合是不可数的,所以有如下推论:
6.3 正则表达式
搜索 一段文本是计算中的一个常见任务. 从本质上说, 搜索问题 非常简单.
我们有一个串集(例如硬盘上的文件,或数据库中的学生记录),而用户想要找到一个所有被某些模式 匹配 的构成的子集.
(例如,所有名称以串.txt结尾的文件)
在最一般的情况下,我们允许用户通过指定一个(可计算的) 函数 来指明模式,其中与的模式匹配相一致.
这就是说,用户提供一个用像 Python 这样的编程语言编写的 程序 ,而系统返回所有使的
举例而言,我们可以搜索所有包含串important document的文本文件,或是(让与一个基于神经网络的分类器相一致)所有包含猫的图片.
然而,我们希望系统不会为了尝试求程序的值,而因此陷入死循环!
因此,典型的搜索文件和数据库的系统 不 允许用户用功能齐全的编程语言来指定模式.
相反,这样的系统使用 受限计算模型 . 这种模型一方面 足够丰富 ,可以捕捉许多实践中需要的查询(例如,所有以.txt结尾的文件名,或者所有形如(617)xxx-xxxx的电话号码),但另一方面受到的 限制 又足够大,使大型文件中的查询变得非常高效,并避免其陷入死循环.
这种计算模型中最流行的一种是正则表达式. 如果你使用过一个高级的文本编辑器,一个命令行终端,或者进行过任何种类的、对文本文件的大批量操作,那么你很有可能对正则表达式有所耳闻.
在字母表上定义的 正则表达式 由上的元素通过连接操作,操作(与 或 一致)和操作(与重复零到多次一致)组合而成. 举例而言,接下来的正则表达式在字母表上定义,并与所有使每个数位重复至少两次的串所构成的集合一致:
下列正则表达式定义在字母表上,并与所有这样的串形成的集合一致——该串由两个序列连接: 第一个序列由至少一个-的字母形成; 第二个序列由至少一个数位形成(无前导零).
形式化地说,正则表达式由以下递归定义所定义:
在能从上下文中推断出来时,我们也会忽略括号. 我们也使用或运算和连接运算左结合的惯例,并且给运算最高的优先级,然后是连接,最后是或. 因此,举例来说,我们写的是而不是
每个正则表达式都与一个函数一致,其中若 匹配 正则表达式,则 举例说,若 则 而 (你知道为什么吗)
上述的定义本身并不是什么难事,但很麻烦. 所以你应该在此处停下并再看一次上述定义,直到你理解为什么该定义与我们对正则表达式的直观概念是相一致的. 这不仅对理解正则表达式本身(在许多应用中经常使用)很重要,对更好地理解一般的递归定义也一样.
若一个布尔函数在输出时,所有的输入串都能够被某些正则表达式匹配,就说这个布尔函数是“正则的“.
正则表达式可以在任意有限字母表上定义. 但是和之前一样,我们主要关注 二进制情况 ,其中 绝大部分(如果不是所有的话)关于正则表达式的理论和实践的真知灼见都可以从研究二进制情况得到.
6.3.1 匹配正则表达式的算法
除非能计算以下问题,否则正则表达式在搜索方面并不会很有用: 给定一个正则表达式,串是否被匹配. 幸运的是,这样一个算法存在. 准确地说,存在一个算法(你可以想成“Python程序“,尽管稍后就会用 图灵机 来形式化算法的概念),该算法输入一个正则表达式和串,当且仅当匹配时输出(即,输出
实际上,定义 6.3已经指明了一个 计算 的递归算法. 准确地说,操作——连接,或,星号3——可以被视作这样一个过程: 对测试某个表达式是否匹配的任务,将其归约到测试的某个子表达式是否匹配的某个子串. 因为这些子表达式总是比原式短,所以这个判定是否匹配的递归算法最终会在最基础的表达式上停止: 与空串或者当个符号一致.
以上代码假定已经编写了一个过程,其当且仅当匹配空串时输出
一个关键的观察结果为,在对正则表达式的递归定义中,无论是由一个还是两个表达式组成的,这两个正则表达式都比 小 最终(当其长度为时,它们一定和单个字母的非递归情形一致. 相应地,算法 6.1中的递归调用总是和一个更短的表达式或者(在表达式具有形式的情况下)一个更短的输入串相一致. 因此,当输入具有形式时,通过在上做递归,可以证明算法 6.1的正确性. 归纳奠基是或为单独的一个字母,或 在表达式具有形式或时,用更短的表达式做递归调用 在表达式具有形式时,在一个更短的字符串与同样的表达式,或更短的表达式与一个字符串上做递归调用,其中的长度小于等于
对练习 6.3的解答
对练习 6.3的解答
可以通过以下观察结果给出这样一个递归算法
- 具有形式 或的表达式总是匹配空串
- 具有形式 ,其中是一个字母,不匹配空串
- 正则表达式不匹配空串
- 具有形式的表达式当且仅当或匹配空串时才匹配
- 具有形式的表达式当且仅当和都匹配空串时才匹配
根据以上的观察结果,可以给出下列算法来判断是否匹配空串
算法 6.2 (匹配空串).5
6.4 高效匹配正则表达式(可选)
算法 6.1并不高效 举例而言,给定一个包含连接或“*“操作的表达式和一个长度为的串,它需要次递归调用. 因此,在最劣情况下,算法 6.1花费的时间是输入串长度的 指数 级别. 幸运的是,有快得多的算法可以在 线性 时间(即内匹配正则表达式. 鉴于还没提到时间和空间复杂度的话题,我们将像在编程入门课程和白板编程面试中做的那样,不给出计算模型,而使用高级术语描述这个算法,其中使用的运行时间的概念是口语化的. 我们将会在第13章中介绍时间复杂度的形式化定义
定理 6.4中术语所隐含的常数取决于表达式 因此,另一个描述定理 6.4的方法是对于每个表达式,都会有一个常数和一个算法使得在位输入上计算最多需要步 因为在实践中,通常希望对一个短的正则表达式和大的文档计算,所以这是有意义的. 定理 6.4告诉我们,可以在运行时间随文档大小线性增大的情况下计算,即使运行时间可能更依赖于正则表达式的大小
我们通过给出一个高效的递归算法来证明定理 6.4. 该算法将判定是否匹配串的任务归约到判定相关表达式是否匹配 该算法使得表达式的运行时间拥有形式解得
正则表达式的限制: 定理 6.4背后的算法,其中心定义是正则表达式的 限制 的概念 其思想为: 对每个正则表达式和字母,有可能定义一个正则表达式使得匹配当且仅当匹配匹配串 例如,如果是正则表达式(即出现一次或多次),那么与等价而为 (你能发现是为什么吗)
算法 6.3计算给定正则表达式和字母的限制 该算法总会结束,因为其递归调用时传递的表达式总比输入的表达式小. 其正确性可以通过对正则表达式的长度进行归纳证明,归纳奠基是为,,或一个单独的字母时.
通过限制的概念,可以定义如下匹配正则表达式的递归算法
根据限制的定义,对于每个和,表达式匹配当且仅当匹配 因此对每个和,和算法 6.4确实给出了正确的结果. 剩下的唯一任务就是分析其 运行时间 . 需要注意的是,算法 6.4在归纳奠基时使用练习 6.3中的过程. 然而,因为这个过程的运行时间只依赖于,与原输入的长度无关,所以没有问题.
简单起见,我们将注意力限制在字母表与相等的情况. 定义为,给定最大符号数,输入定义在上的符号数不超过最大符号数的正则表达式,算法 6.3所能进行的最大操作次数. 可以发现的值是关于的多项式. 然而这对我们的定理并不重要,因为我们只关心计算时运行时间对长度的依赖而不关心其对长度的依赖.
算法 6.4是输入表达式和串的递归算法. 其计算过程为在最多运行后,以某些表达式和长度为的串为输入调用自身. 它将在步运行后结束,此时它到达一个长度为的串. 因此,对长度为的输入,用算法 6.3计算的运行时间满足以下递归方程:
(在归纳奠基时,是某个只与有关的常数. )
为了对(6.2)有直观印象,我们展开一层递归,将写作
如此继续,可以发现,其中是这么做时会遇到的最长的表达式的长度. 因此,如下声明足以说明算法 6.4在运行时间是
对上述声明的证明
对上述声明的证明
对于一个定义在上的正则表达式和,我们用来指代表达式,其通过将限制在上,再是,以此类推得到. 令 通过说明对每个,集合是有限的,因此也一样,其为中的最大长度,从而证明该声明.
我们通过在的结构上做归纳证明这一点. 如果是符号,空串,或者空集,则可以直截了当地说明能含有的最多的表达式就是只有这个表达式本身,和 对其余情况,我们分为两类: (i) 和 (ii) ,其中是更小的表达式(因此根据归纳假设和有限).
在情况 (i) 中,若则要么等于要么在时为空集合. 因为在集合中,所以中不同表达式的个数最多为
在情况 (ii) 中,若,则在串上的所有限制要么具有形式,要么具有形式,其中为使得成立的串,其中 匹配空串.
因为 和 ,所以具有形式的可能不同的表达式的数量最多有个. 这就完成了对该声明的证明.
最重要的是,在一个正则表达式上运行算法 6.4时,会遇到的所有表达式都在有限集中,不论输入多大. 因此算法 6.4的运行时间满足等式,其中是依赖于的常数. 最终解得,O记号中隐含的常数可以(且将会)依赖于,并且,重要的是,不依赖于输入的长度.
6.4.1 用DFAs匹配正则表达式
定理 6.4非常令人印象深刻,但是我们可以做得更好. 准确的说,不管有多长,都可以通过维护一个常数大小的内存并进行对的 单次遍历 来计算 也就是说,这个算法将会从输入的开头扫描到结尾,然后判定是否被匹配. 在常见情况下,我们会尝试在巨大的文件或文档中匹配简短的正则表达式,这些文件或文档甚至没法整个装在电脑的内存里,此时这一特点尤为重要. 当然,如前所述,一个单遍常数内存算法仅仅就是一个确定性有穷自动机. 就像在定理 6.6中将要看到的那样,一个函数能被正则表达式计算 当且仅当 它能被一个DFA计算. 我们从证明“仅当“开始:
对定理 6.5的证明思路
对定理 6.5的证明思路
对定理 6.5的证明
对定理 6.5的证明
算法 6.5判定给定的串是否被正则表达式所匹配.
对每个正则表达式,这个算法都有恒定数量的布尔变量(更准确地说,对每个有一个变量和 该算法利用了一个事实: 对每个,都在中. ) 其对输入串进行单次遍历. 因此与一个DFA一致.
我们通过归纳输入长度来证明其正确性. 准确地说,我们将论证,在读入之前,对每个,变量与相等.
因为初始对每个,让所以的情况成立 对的情况,归纳法证明其成立. 归纳假设表明对每个,都有 而根据集合的定义,对每个,和,位于中而
6.4.2 正则表达式和自动机的等价性
回忆 以下,若存在某个正则表达式,布尔函数与相等,则称其为 正则的 . (等价地,若存在某个正则表达式,语言满足当且仅当时匹配,则称其为 正则的 ). 下述定理是自动机理论的核心:
对定理 6.6的证明思路
对定理 6.6的证明思路
对定理 6.6的证明
对定理 6.6的证明
既然定理 6.5已经证明了“仅当“方向,现在只需要证明“当“方向. 令为一个状态DFA,其计算函数,需要证明是正则的.
对每个,令为这样的函数: 当且仅当DFA 从状态出发,读入输入后会到达状态,则其将映射到 现在将要证明对每个都正则. 这将证明该定理. 因为根据定义 6.1,等于对所有取或,其中 因此一旦能够为每个具有形式的函数写出一个正则表达式,(通过使用操作)也就可以得到的正则表达式.
为了给出函数的正则表达式,现在从定义函数开始: 对每个和,当且仅当自动机从出发接受输入后到达且 *所有的中间状态都在集合中 . (见图 6.7)
这就是说,尽管可能会在之外,当且仅当在输入(从出发)时自动机运行过程中永不进入之外的状态并在结束. 当时就是空集,因此当且仅当自动机在输入时直接从转移到而不经过任何的中间状态. 当时所有的状态都在中,因此
现在通过归纳来证明这个定理,说明对所有和,正则.
对于 归纳奠基 ,对所有的,都正则,因为它可以被表示为表达式,,,或中的一个.
准确地说,若,则当且仅当为空串. 若,则当且仅当为单个字母且
因此在这种情况中,与四个正则表达式,,和中的一个相一致,并取决于从转移到时读取的是或,还是仅为两个符号中的一者,或者都不是.
归纳步骤 : 刚刚已经说明了归纳奠基,现在通过归纳法来证明一般情况. 归纳假设为对每个,都有正则表达式计算 需要证明的是对每个,正则. 如果自动机从到时访问了中间状态,则其访问了第个状态零次或多次.
如果一个路径标号为,使得自动机从到,并且过程中不需要访问第个状态,则被正则表达式匹配; 如果一个路径标号为,使得使得自动机从到,并且过程中需要访问第个状态次,则可以将该路径视为:
- 首先,从到,期间访问的中间状态均位于
- 然后,回到自身次,期间访问的中间状态均位于
- 最后,从到,期间访问的中间状态均位于
因此在该情况下,字符串被正则表达式匹配. (又见图 6.8) 因此可以使用以下正则表达式计算
归纳步骤证明完毕,进而定理得证明.
6.4.3 正则表达式的闭包性质
若和分别是被和计算的正则函数,则表达式计算函数 其定义为 另一个说法是,正则函数族 在或运算下封闭 . 这就是说,如果和正则,则也一样. 定理 6.6的重要推论是这个集合也在非运算下封闭
因为,引理 6.1表明正则函数族在与操作下也同样封闭. 进一步说,因为或,非,与是通用的基础运算,这个集合在与非,异或,和其它有限函数的运算下也封闭. 这就是说,我们有如下推论
6.5 正则表达式的限制与泵引理
正则表达式的高效匹配使其分外实用. 通常来说,操作系统和文本编辑器都限制其搜索接口,不允许任意指明一个函数,并采用正则表达式,其原因就在此处. 然而,这种高效是有代价的. 如我们所见,正则表达式无法计算所有函数. 实际上,有很多简单(而且有用! )的函数无法被正则表达式计算. 以下是一个样例:
引理 6.2是如下结果的一个推论,该结果也被称为泵引理 :
对定理 6.8的证明思路
对定理 6.8的证明思路
对定理 6.8的证明
对定理 6.8的证明
通过归纳表达式的长度可以形式化地证明该引理.
像所有的归纳证明一样,该证明会比较长,但在结尾给出符合我们直觉结果——我们一定在某处使用了闭包运算. 阅读该证明,特别地,去理解以下的形式化证明如何与上面的直观思路相一致,是更好地熟悉该种归纳证明的好方法.
归纳假设为对于一个长度为的表达式,符合引理要求的条件.
归纳奠基 为当表达式为当个字母或者或 在这些情况中引理显然成立,因为,而不可能有长度大于的串被该表达式匹配.
我们现在证明 归纳步骤 . 令为有个符号的正则表达式,让且串满足 既然有多于一个符号,则其具有下列形式之一: (a) : (b) : (c) 在所有情况中,子表达式与的符号数都少于,因此符合归纳假设.
在情况 (a) 中,每个被匹配的串都被与中的一者匹配. 若匹配,则根据归纳假设以及,有,其中与使得对每个,(因此也一样)匹配 当匹配时同理.
在情况 (b) 中,若被匹配,则有,其中匹配而匹配 我们现在分类讨论. 若则根据归纳假设有满足,使得,且对每个有匹配 如果我们令,则,且对于每个有匹配 否则,若,又,则必定有 因此根据归纳假设有使得,且对每个有匹配 而我们现在令,则有 而另一方面对每个,表达式匹配
在情况 (c) 中,若被匹配,则,其中对每个,是一个被匹配的非空串. 若,我们可以用与上述连接运算情况相同的方法. 否则,注意到若是空串,且则且对每个,被匹配.
通过泵引理,我们可以轻易地证明引理 6.2(即“括号匹配“函数的非正则性):
对引理 6.2的证明
对引理 6.2的证明
对于一个确定的函数,在说明该函数 不能 被正则表达式计算的方面,泵引理是一个有效的工具. 然而,这并 不是 正则性的“充分必要“条件: 存在一个非正则的函数,其满足泵引理的条件. 为了理解泵引理,遵循定理 6.8中量词的顺序是很关键的. 特别地,定理 6.8所描述的数字取决于所选的正则表达式(上述证明选择了表达式所用符号数的两倍). 所以,为了使用泵引理来排除计算某个函数的正则表达式的存在性,就需要能够选择一个合适的输入 它要能够任意地增大,并且满足F(w)=1. 如果你仔细思考泵引理后蕴含的直观,就会发现上述内容是很有意义的: 足够大的才能强制性地要求使用闭包运算.
对练习 6.4的解答
对练习 6.4的解答
此处采用泵引理. 为了使用反证法,假设有一个正则表达式计算,令为泵引理(定理 6.8)中的数. 考虑串 因为全部由零组成的串的反转仍为全部由零组成的串,所以 现在,根据选择引理,如果被计算,则可以写下使得,且对每个有 特别地,一定成立,但这就导致了矛盾,因为,所以其两部分并不一样长,所以并不是另一者的反转.
另一个基于泵引理的证明见图 6.10,这是一个关于函数非正规性证明的漫画,其中当且仅当存在使得(即,为一个连续零串拼接上一个同等长度的连续一串).
6.6 回答正则表达式的语义问题
正则表达式有着除搜索之外的其他应用. 例如,在编程语言的 语法分析器 、 编译器 和 解释器 的设计中,正则表达式通常用于定义 词元 (例如一个有效的变量名,或者关键字). 正则表达式还有别的应用: 例如,近年来,互联网从固定的拓扑结构演化为“软件定义的网络“. 这样一个网络由可编程交换机进行路由,这些交换机实现了一些 策略 ,例如“如果包被SSL验证,则把它转发到A,否则转发到B“. 为了表示这样的策略,我们需要一种语言,它一方面足够丰富,可以捕捉我们需要实现的策略; 另一方面又被充分地限制,从而可以在网络高速的要求下快速地执行它们,并能够回答像“C能否查看从A到B的包“这样的问题.
NetKAT网络编程语言通过正则表达式的一个变体来精确地实现这一点. 在这些应用中,我们不仅仅能够回答表达式能够匹配,同时也回答关于正则表达式的 语义问题 ,例如“表达式和是否计算同一个函数“ 以及 “是否存在串被匹配? “
接下来的定理说明我们可以回答后者:
对定理 6.9的证明思路
对定理 6.9的证明思路
思路为,我们可以直接从表达式的结构中观察到这一点. 计算常零函数的唯一可能是具有形式或者通过与其他表达式连接得到.
对定理 6.9的证明
对定理 6.9的证明
如果一个正则表达式计算的是常零函数,我们就定义其是“空的“. 给定一个正则表达式,通过以下规则,我们可以判定是否为空:
- 若具有形式或,则其非空
- 若非空,则对所有的,均非空
- 若非空则非空
- 若与均非空,则非空.
- 为空.
通过这些规则,可以直接得出一个判定空性的递归算法.
通过定理 6.9,我们可以得到判定两个正则表达式是否 等价 的算法. 这意味着它们计算相同的函数.
对定理 6.10的证明思路
对定理 6.10的证明思路
证明思路是,对于给定的一对正则表达式,,我们寻找一个表达式使得当且仅当 因此为常零函数当且仅当与等价,则我们可以由此通过测试的空性来判定与的等价性.
对定理 6.10的证明
对定理 6.10的证明
我们从定理 6.9中证明定理 6.10. (这两个定理实际上是等价的: 我们很容易从定理 6.10中证明定理 6.9,因为测试表达式空性和判定其与的等价性是一样的. )
对给定的两个表达式与,目标是计算表达式使得当且仅当 可以发现,与等价当且仅当为空.
我们从这样一个观察结果出发: 对每个位 ,当且仅当
因此我们需要构造这样一个,其对所有的,均有
为了构造这个表达式,我们会说明对于任意一对和,我们可以构造表达式与,其分别计算和 (计算表达式是很直接的,只需使用运算)
特别地,根据引理 6.1,正则函数在否运算下封闭. 这意味着对每个正则表达式,均有表达式使得对所有均有
于是,对于所有的两个表达式与,表达式 计算表达式的与运算.
给出了这两个变换,可以发现对所有的正则表达式与,都可以找到一个表达式满足(6.3),使得为空当且仅当与等价.
- 使用 无限 函数对输入长度任意的计算任务建模.
- 这样一种函数输入一个任意长(但仍然有限! )的串,而且不能被一个由输入输出构成的有限表格描述.
- 被称为 布尔函数 的一类特殊函数,其输出为单个位. 计算该函数等价于判定一个 语言
- 确定性有穷自动机 (DFAs)是计算(无限)布尔函数的一个简单模型.
- 有一些函数无法被DFAs计算.
- DFAs可计算的函数族与正则表达式能识别的语言族相同.
6.7 习题
6.8 参考文献
正则表达式与有穷自动机的练习是一个优美的话题,本文中我们对其浅尝辄止. (Sipser, 1997)(Hopcroft, Motwani, Ullman, 2014)(Kozen, 1997)中对该话题涉及更多. 这些文章也讨论了像 非确定有穷自动机 (NFA),以及上下文无关文法与下推自动机的关系.
图 6.4中的自动机由FSM simulator生成,作者为Ivan Zuzak和Vedrana Jankovic.
我们对于定理 6.4的证明与Myhill-Nerode定理联系紧密. Myhill-Nerode定理的一个方向可以被陈述为: 如果是一个正则表达式,则存在最多有限个串,使得对每个,有
1: 译者注: 中的元素称为 字母 ,原著中提到其元素时使用的术语是字母表符号alphabet symbol,翻译时为了简洁使用字母这一个更加简单的术语
2: 译者注: 更准确地说,是条,但之后考虑的均为,因此
3: 译者注: 准确的说法是闭包
4: 译者注: 事实上,以上过程仅仅证明了算法 6.1是会结束的,但是并没有证明正确性. 但上面的过程确实给出了证明其正确性的骨架,因此剩下的工作繁而不难
5: 译者注: 该算法并未要求输入串 此处应为作者笔误
6: 译者注: 此处应为作者笔误,正确语句应当如下: 且有一个非空子串被匹配,其中为的子串.
- 等价的计算模型
等价的计算模型
学习目标
- 了解RAM机(RAM Machine)与λ演算(λ Calculus)
- 掌握这些模型与图灵机及其他模型的等价关系
- 认识元胞自动机(Cellular Automata)与各种图灵机格局
- 理解Church-Turing论题
由于后续我们将使用函数表达式进行计算, 必须区分函数与形式, 并需要相应的表示法. 这一区分及其描述记法由Church提出, 我们仅作细微调整.
——约翰·麦卡锡(John McCarthy), 1960年(摘自描述LISP编程语言的论文)
到目前为止, 我们已经定义了使用图灵机计算函数的概念, 但这与实际的计算方法并不完全吻合. 本章将通过证明可计算函数的定义在各种计算模型下保持不变, 来论证这一选择的合理性. 这一概念被称为图灵完备性(Church completeness)或图灵等价性(Church equivalence), 是计算机科学中最基本的事实之一. 实际上, 被广泛认同的Church-Turing论题做了出了如下主张: 任何对可计算函数的“合理“定义, 都等价于通过图灵机可计算的概念. 我们将在8.8节讨论Church-Turing论题以及“合理“的可能定义.
本章讨论的主要计算模型包括:
- RAM机: 图灵机与具备随机存取存储器(RAM, Random Access Memory)的标准计算架构并不对应, RAM机的数学模型更接近实际计算机, 但我们将看到它在计算能力上与图灵机等价. 我们还将讨论RAM机的一种编程语言变体, 称之为NAND-RAM. 图灵机与RAM机的等价性使得我们能够证明诸多流行编程语言的图灵等价性, 包括现实中使用的所有通用编程语言, 如C、Python、JavaScript等.
- 元胞自动机: 许多自然的和人工的系统都可以被建模为简单组件的集合, 每个组件根据其自身状态及其直接邻居的状态, 按照简单的规则进行演化. 一个著名的例子是康威的生命游戏(Conway’s Game of Life). 为了证明元胞自动机与图灵机等价, 我们将引入图灵机格局(configurations of Turing machines). 这些格局还有其他应用, 特别是在第11章用于证明哥德尔不完备定理——数学中的一个核心结果.
- λ演算: λ演算是一种表达计算模型, 起源于20世纪30年代, 不过它与当今广泛使用的函数式编程语言密切相关. 证明λ演算与图灵机等价涉及一种名为“Y组合子“(Y Combinator)的消除递归的巧妙方法.
本章中我们将研究不同模型间的等价性. 如果两个计算模型能够计算的函数构成的集合是相同的, 则称它们是等价的(也称之为图灵等价). 例如, 我们已经看到图灵机与NAND-TM程序是等价的, 因为我们可以将每个图灵机转换为计算相同函数的NAND-TM程序, 同样地, 也可以将每个NAND-TM程序转换为计算相同函数的图灵机.
本章我们将证明这种等价性远不止于图灵机. 我们开发的技术使我们能够证明所有通用编程语言(即Python、C、Java等)都是图灵完备的, 即它们能够模拟图灵机, 因此能够计算所有图灵机可计算的函数. 我们还将证明其反向亦成立——图灵机可以用来模拟用任何这些语言编写的程序, 因此能够计算这些语言可计算的任何函数. 这意味着所有这些编程语言都是图灵等价的: 即它们在计算能力上等价于图灵机, 并且彼此等价. 这是一个强大的原理, 是计算机科学广泛影响的基础. 此外, 它使我们能够“鱼和熊掌兼得“——既然所有这些模型都是等价的, 我们可以为手头的任务选择方便的模型. 为了实现这种等价性, 我们定义了一种新的计算模型, 称为RAM机. RAM机比图灵机更接近现代计算机的架构, 但在计算能力上仍然与图灵机等价.
最后, 我们将证明图灵等价性远不止于传统编程语言, 作为极其简单的自然系统的数学模型的元胞自动机也是图灵等价的, 并且我们还将看到λ演算的图灵等价性——λ演算是一种用于表达函数的逻辑系统, 是Lisp、OCaml等函数式编程语言的基础.
本章成果概览见图 8.1.
8.1 RAM机与NAND-RAM
图灵机(以及NAND-TM程序)的一个局限性在于, 我们每次只能访问数组或磁带的一个位置. 如果磁头位于磁带的第位, 而我们想要访问第个位置, 那么我们至少需要步才能到达该位置. 相比之下, 几乎每种编程语言都提供了直接访问内存位置的形式化方法. 实际的物理计算机也提供了可以被视为一个大型数组Memory的随机存取存储器(RAM), 给定索引(即内存地址或指针), 我们可以读取和写入Memory的第个位置. (“随机存取存储器“这一名称实际上用词有误, 因为它与概率无关, 但既然这是计算理论与实践中的标准术语, 我们也将沿用这一说法).
中这种内存访问进行建模的计算模型是RAM机(有时也称为字RAM模型(Word RAM Model)), 如图 8.2所示. RAM机的内存是一个大小无界的数组, 其中每个单元可以存储一个字(Word), 我们将其视为的字符串, 同时(等价地)也视为中的一个数字. 例如, 许多现代计算架构使用64位的字, 每个内存位置保存一个中的字符串, 这也可以视为一个介于到之间的数字. 参数被称为字长(Word Size). 在实践中, 通常是一个固定数字(比如64), 但在理论研究中, 我们将建模为一个可以依赖于输入长度或步骤数的参数. (你可以将大致视为我们在计算中使用的最大内存地址)除了内存数组, RAM机还包含恒定数量的寄存器(Register) 每个寄存器也能保存一个字.
RAM机可以执行的操作包括:
- 数据移动: 将内存中某个单元的数据加载到寄存器中, 或将寄存器的内容存储到内存的某个单元. RAM机可以直接访问内存的任何单元, 而无需像图灵机那样将“磁头“移动到该位置. 也就是说, RAM机可以在一步中将由寄存器索引的内存单元的内容加载到寄存器中, 或将寄存器的内容存储到由寄存器索引的内存单元中.
- 计算: RAM机可以对寄存器执行计算, 例如算术运算、逻辑运算和比较.
- 控制流: 与图灵机一样, 接下来执行什么指令的选择可以取决于RAM机的状态, 这由其寄存器的内容捕获.
我们不会给出RAM机的正式定义, 但参考文献部分(第8.10节)包含了这些定义的来源. 正如NAND-TM编程语言模拟图灵机一样, 我们也可以定义一种模拟RAM机的NAND-RAM编程语言. NAND-RAM编程语言通过添加以下特性扩展了NAND-TM:
- NAND-RAM的变量允许是(非负)整数值的, 而不仅仅是NAND-TM中的布尔值. 也就是说, 标量变量
foo保存的是中的非负整数(而不仅仅是中的一位), 数组变量Bar保存的是一个整数数组. 与RAM机的情况一样, 我们不允许无界大小的整数. 具体来说, 每个变量保存一个介于和之间的数字, 其中是程序到目前为止已执行的步骤数. (你现在可以忽略此限制: 如果我们想要保存更大的数字, 可以简单地执行虚拟指令;这在后面的章节中会有用) - 我们允许对数组进行索引访问. 如果
foo是标量而Bar是数组, 则Bar[foo]引用由foo的值索引的Bar的位置. (注意这意味着我们不再需要特殊的索引变量i) - 正如编程语言中常见的情况, 我们假设对于布尔运算(如
NAND), 零值整数被视为假, 非零值整数被视为真. - 除了
NAND之外, NAND-RAM还包括所有基本的算术运算: 加、减、乘、(整数)除, 以及比较(等于、大于、小于等). - NAND-RAM将条件语句
if/then作为语言的一部分. - NAND-RAM包含循环结构, 例如
while和do, 作为语言的一部分.
NAND-RAM编程语言的完整描述见附录. 然而, 关于NAND-RAM你需要了解的最重要的事实是你实际上并不需要太多了解NAND-RAM, 因为它在能力上等同于图灵机:
由于NAND-TM程序等价于图灵机, 而NAND-RAM程序等价于RAM机, 定理 8.1表明所有这四种模型彼此之间是等价的.
定理 8.1的证明思路
定理 8.1的证明思路
显然, NAND-RAM只会比NAND-TM更强大, 因此如果一个函数可由NAND-TM程序计算, 那么它也能由NAND-RAM程序计算. 具有挑战性的方向是将NAND-RAM程序转换为等价的NAND-TM程序 要完整描述这个证明, 我们需要涵盖NAND-RAM语言的完整形式化规范, 并展示如何将其每一个特性实现为NAND-TM之上的语法糖.
这可以做到, 但详细检查所有操作相当繁琐. 因此, 我们将着重描述此转换背后的主要思想. (另见图 8.4)NAND-RAM在两个方面推广了NAND-TM: (a) 增加了对数组的索引访问(即Foo[bar]语法), 以及 (b) 从布尔值变量过渡到整数值变量. 该转换有两个步骤:
- 位数组的索引访问: 我们首先展示如何处理 (a). 即, 我们展示如何在NAND-TM中实现操作
Setindex(Bar), 使得如果Bar是编码了某个整数的数组, 则在执行Setindex(Bar)后,i的值将等于 这将允许我们通过Setindex(Bar)后跟Foo[i]来模拟Foo[Bar]这种形式的语法. - 二维位数组: 接着, 我们展示如何使用“语法糖“来为NAND-TM增加二维数组的功能. 即, 拥有两个索引
i和j以及二维数组, 使得我们可以使用语法Foo[i][j]来访问Foo的(i,j)位置. - 整数数组: 最后, 我们将一个整数的一维数组
Arr编码为一个位的二维数组Arrbin. 思路很简单: 如果是Arr[]的一个二进制(无前缀)表示, 那么Arrbin[][]将等于
一旦我们有了整数数组, 我们就可以使用我们常用的函数语法糖、GOTO等来实现NAND-RAM的算术和控制流操作.
上述方法并非获得定理 8.1证明的唯一途径, 例如可参见练习8.1.
RAM机与现实中的微处理器(例如Intel x86系列中的那些)非常对应, 这些微处理器也包含一个大的主内存和数量固定的少量寄存器. 这当然并非偶然: 与图灵机相比, RAM机旨在更贴近地模拟实际计算系统的体系结构, 这种体系结构在很大程度上遵循了 (von Neumann, 1945) 报告中描述的所谓冯·诺依曼架构. 因此, NAND-RAM在其大致轮廓上类似于x86或NIPS等汇编语言. 这些汇编语言都具有以下指令: (1) 将数据从寄存器移动到内存, (2) 对寄存器执行算术或逻辑计算, 以及 (3) 条件执行和循环(在汇编语言语境中通常称为“分支“和“跳转“的“if“和“goto“).
RAM机与实际微处理器之间的主要区别(相应地, 也是NAND-RAM与汇编语言之间的主要区别)在于, 实际微处理器具有固定的字长 因此所有寄存器和内存单元保存的都是中的数字(或等价地, 中的字符串). 这个数字在不同的处理器中可能不同, 但常见的值要么是 要么是 作为理论模型, RAM机没有这个限制, 我们反而让作为我们运行时间的对数(这也大致对应于其在实践中的值). 现实中的微处理器也具有固定数量的寄存器(例如, x86-64中有14个通用寄存器), 但这与RAM机相比差别不大. 可以证明, 只有两个寄存器的RAM机与拥有任意大的常数数量寄存器的完整RAM机具有同等能力.
当然, 现实中的微处理器也具有许多RAM机所不具备的特性, 包括并行性、内存层次结构以及许多其他特性. 然而, RAM机确实在初步近似下捕捉了实际计算机的特征, 因此(正如我们将看到的), 算法在RAM机上的运行时间(例如, 对比与其实际运行的效率高度相关.
8.2 具体细节(可选)
我们将不展示定理 8.1的完整形式化证明, 而是聚焦于最重要的部分: 实现索引访问, 以及用一维数组模拟二维数组. 即便如此, 描述这些部分也已经相当繁琐, 这对于任何写过编译器的人都不足为奇. 因此, 你可以随意略读本节. 重点不在于记住所有细节, 而在于明白原则上将一个NAND-RAM程序转换为等价的NAND-TM程序是可能的, 你自己如果想做也能完成.
8.2.1 NAND-TM中的索引访问
在NAND-TM中, 我们只能访问数组在索引变量i位置处的元素, 而NAND-RAM拥有整数值变量, 并能使用它们对数组进行索引访问, 写作Foo[bar]. 为了在NAND-TM中实现索引访问, 我们将使用某种无前缀编码(参见2.5.2节)在数组中编码整数, 然后提供一个过程Setindex(Bar)来将i设置为Bar编码的值. 我们可以通过先执行Setindex(Bar)再执行Foo[i]来模拟Foo[Bar]的效果.
Setindex(Bar)的实现可以通过以下方式完成:
- 初始化一个数组
Atzero, 使得Atzero[]并且对所有Atzero[](这可以在NAND-TM中轻松完成, 因为所有未初始化的变量默认值为零) - 通过递减
i直到达到Atzero[i]的点来将i设置为零. - 令
Temp为一个编码数字的数组. - 我们使用
GOTO来模拟一个内部循环, 形式如下: 当TempBar时, 递增Temp. - 在循环结束时,
i等于由Bar编码的值.
在NAND-TM代码中(使用一些语法糖), 我们可以按如下方式实现上述操作:
# 假设Atzero是一个数组, 满足Atzero[0]=1
# 且对所有j>0, Atzero[j]=0
# 将i设置为0.
LABEL("zero_idx")
dir0 = zero
dir1 = one
# 对应i <- i-1
GOTO("zero_idx",NOT(Atzero[i]))
...
# 将temp清零
#(下面的代码假设使用一种特定的无前缀编码, 其中10是"结束标记")
Temp[0] = 1
Temp[1] = 0
# 将i设置为Bar, 假设我们知道如何递增和比较
LABEL("increment_temp")
cond = EQUAL(Temp,Bar)
dir0 = one
dir1 = one
# 对应i <- i+1
INC(Temp)
GOTO("increment_temp",cond)
# 如果执行到这里, i就是Bar所编码的数字
...
# 程序的最终指令
MODANDJUMP(dir0,dir1)
8.2.2 NAND-TM中的二维数组
为了实现二维数组, 我们希望将它们嵌入到一个一维数组中. 思路是通过一个一一对应的函数 从而将二维数组Two中的位置嵌入到一维数组One的位置中.
由于集合看上去“远大于“集合 先验地来看, 这样的一个双射可能并不明显存在. 然而, 一旦你深入思考, 你就会发现构建它并不算太难. 例如, 你可以让一个孩子用剪刀和胶水将一张10英寸乘10英寸的纸转换成一条1英寸乘100英寸的纸带. 这本质上就是一个从到的双射. 我们可以推广这一点, 得到一个从到的双射, 更一般地, 得到一个从到的双射.
具体来说, 下面的函数可以做到这一点(见图 8.5):
习题8.3要求你证明确实是一个双射, 并且可以由一个NAND-TM程序计算. (后者可以通过简单地遵循小学所学的乘法、加法和除法算法来完成)这意味着我们可以将形式为Two[Foo][Bar] = something(即, 访问二维数组中由一维数组Foo和Bar编码的整数对应的位置)替换为如下形式的代码:
Blah = embed(Foo,Bar)
Setindex(Blah)
Two[i] = something
8.2.3 其他细节
一旦我们有了二维数组和索引访问, 用NAND-TM模拟NAND-RAM就只是在NAND-TM中实现算术运算和比较的标准算法的问题了. 虽然这很繁琐, 但并不困难, 最终的结果表明每个NAND-RAM程序都可以被一个等价的NAND-TM程序模拟, 从而完成了定理 8.1的证明.
递归是许多编程语言中都出现的一个概念, 但我们没有将其包含在NAND-RAM程序中. 然而, 递归(以及一般的函数调用)可以在NAND-RAM中使用栈数据结构来实现. 栈是一种包含一系列元素的数据结构, 我们可以按照“后进先出“的顺序向其中“压入“元素和从中“弹出“元素.
我们可以使用一个整数数组Stack和一个标量变量stackpointer(表示栈中的项目数量)来实现一个栈. 我们通过以下方式实现push(foo):
Stack[stackpointer]=foo
stackpointer += one
并通过以下方式实现bar = pop():
bar = Stack[stackpointer]
stackpointer -= one
我们通过将的参数压入栈中来实现对的函数调用. 的代码将从栈中“弹出“参数, 执行计算(可能涉及进行递归或非递归调用), 然后将其返回值“压入“栈中. 由于栈的“后进先出“特性, 直到所有递归调用完成, 我们才会将控制权返回给调用过程.
我们可以使用非递归语言实现递归这一事实并不令人惊讶. 实际上, 机器语言通常不具有递归(或一般的函数调用)功能, 因此编译器使用栈和GOTO来实现函数调用. 你可以在网上找到关于您最喜欢的编程语言(无论是Python、JavaScript还是Lisp/Scheme)中如何通过栈实现递归的教程.
8.3 图灵等价性(讨论)
任何标准编程语言, 如C、Java、Python、Pascal、Fortran, 其操作都与NAND-RAM非常相似. (事实上, 它们最终都可以由具有固定数量寄存器和大型内存阵列的机器来执行)因此, 使用定理 8.1, 我们可以用NAND-TM程序来模拟任何此类编程语言中的程序. 反过来, 在任何上述编程语言中编写一个NAND-TM的解释器是一个相当简单的编程练习. 因此, 我们也可以使用这些编程语言来模拟NAND-TM程序(进而通过定理7.11来模拟图灵机). 这种在计算能力上等同于图灵机/NAND-TM的特性被称为图灵等价(有时也称为图灵完备). 因此, 我们熟悉的所有编程语言都是图灵等价的. 1
8.3.1 “两全其美“的范式
图灵机与RAM机之间的等价性使我们能够为手头的任务选择最方便的语言:
- 当我们想要证明一个关于所有程序/算法的定理时, 我们可以使用图灵机(或NAND-TM), 因为它们更简单且易于分析. 特别是, 如果我们想证明某个函数无法被计算, 那么我们将使用图灵机.
- 当我们想要证明某个函数可以被计算时, 我们可以使用RAM机器或NAND-RAM, 因为它们更容易编程, 并且更接近于我们习惯的高级编程语言. 事实上, 我们通常会以非正式的方式描述NAND-RAM程序, 并相信读者能够填充细节并将简略的描述转换为精确的程序. (这就像人们通常使用非正式的或“伪代码“的算法描述方式, 并相信他们的受众知道在需要时将这些描述转换为代码一样)
我们对图灵机/NAND-TM和RAM机/NAND-RAM的使用, 与人们在实践中使用高级和低级编程语言的方式非常相似. 当人们想要制造一个执行程序的设备时, 为一种非常简单和“低级“的编程语言来实现是很方便的. 当人们想要描述一个算法时, 使用尽可能高级的形式体系是方便的.
8.3.2 浅谈抽象层次
程序员处于一个独特的位置……他必须能够思考概念层次结构, 其深度是单个思维以前从未需要面对的.
*——Edsgar Dijkstra, 《论真正教授计算机科学的残酷性》, 1988年. *
在任何计算理论课程中的某个时刻, 教师和学生都需要进行那次谈话. 也就是说, 我们需要讨论描述算法时的抽象层次. 在算法课程中, 通常用英语描述算法2, 假设读者能够“填充细节“, 并在需要时能够将此类算法转化为实现. 例如, 算法 8.1是广度优先搜索算法的高级描述.
如果我们想提供关于如何在Python或C(或NAND-RAM/NAND-TM)等编程语言中实现广度优先搜索的更多细节, 我们会描述如何用数组实现队列数据结构, 以及同样如何用数组标记顶点. 我们称这种“中间层次“的描述为实现级别(implementation level)或伪代码描述. 最后, 如果我们想精确地描述实现, 我们会给出程序的全部代码(或另一个完全精确的表示形式, 例如元组列表的形式). 我们称之为形式化或低级(low level)描述.
虽然我们开始时是在完全形式化的层面上描述NAND-CIRC、NAND-TM和NAND-RAM程序, 随着本书的深入, 我们将转向实现级别和高级别的描述. 毕竟, 我们的目标不是使用这些模型进行实际计算, 而是分析计算的一般现象. 也就是说, 如果你不理解高级描述如何转化为实际实现, “深入底层“通常是一个极好的练习. 计算机科学家最重要的技能之一就是能够在抽象层次结构中上下移动.
类似的区别也适用于将对象表示为字符串的概念. 有时, 为了精确起见, 我们会给出一个低级规范(low level specification), 确切说明一个对象如何映射到二进制字符串. 例如, 我们可能将个顶点的图的编码描述为长度为的二进制字符串, 通过说明我们将顶点集为的图映射到字符串 其中的第个坐标是当且仅当边存在于中. 我们也可以使用中间或实现级别的描述, 只需简单说明我们使用邻接矩阵表示法来表示图.
最后, 因为图(以及一般对象)的各种表示之间的转换可以通过NAND-RAM(因此也可以通过NAND-TM)程序完成, 所以在进行高级别讨论时, 我们也会避免关于表示的讨论. 例如, 图连通性是一个可计算函数, 这一事实无论我们是用邻接表、邻接矩阵、边对列表等表示图都是成立的. 因此, 在精确表示无关紧要的情况下, 我们通常会谈论我们的算法将对象(可以是图、向量、程序等)作为输入, 而不指定如何被编码为字符串.
定义“算法“: 到目前为止, 我们一直非正式地使用“算法“这个术语. 然而, 图灵机和一系列等效模型产生了一种精确且形式化地定义算法的方法. 因此, 在本书中, 每当我们提到算法时, 我们指的是它是图灵等效模型(如图灵机、NAND-TM、RAM机等)中的一个实例. 由于所有这些模型的等价性, 在许多情况下, 我们使用哪一个并不重要.
8.3.3 图灵完备性与等价性的形式化定义(可选)
一个计算模型是某种定义程序(由字符串表示)计算(部分)函数的方式. 一个计算模型是图灵完备的, 如果我们可以将每个图灵机(或等价的NAND-TM程序)映射到中的一个程序 使得计算与相同的函数. 它是图灵等价的, 如果另一个方向也成立(即, 我们可以将中的每个程序映射到一个计算相同函数的图灵机). 我们可以形式化地定义这个概念如下. (这个形式化定义对于本书的其余部分并不关键, 只要你理解图灵等价的一般概念就可以跳过它;这个概念在文献中有时被称为哥德尔数(Gödel numbering)或可接纳数(admissible numbering))
一些图灵等价模型的例子(其中一些我们已经见过, 一些将在下面讨论)包括:
- 图灵机
- NAND-TM程序
- NAND-RAM程序
- λ演算
- 生命游戏(将程序和输入/输出映射到起始和结束格局)
- 编程语言, 如Python/C/Javascript/OCaml…(允许无限存储)
8.4 元胞自动机
许多物理系统可以被描述为由大量相互作用的基元组件组成. 一种模拟此类系统的方法是使用元胞自动机. 这是一个由大量(甚至无限)细胞组成的系统. 每个细胞只有有限个可能的状态. 在每个时间步, 细胞通过将某个简单规则应用于自身及其邻居的状态来更新到新状态.
图 8.9. 康威生命游戏的规则. 图片来自此博客文章
元胞自动机的一个典型例子是康威的生命游戏(Conway’s Game of Life). 在此自动机中, 细胞排列在一个无限二维网格中. 每个细胞只有两种状态: “死亡”(我们可以编码为并标识为或“存活“(我们可以编码为 细胞的下一个状态取决于其先前状态及其8个垂直、水平和对角线邻居的状态(参见图 8.9). 死亡细胞只有在恰好有三个存活邻居时才会变为存活. 存活细胞只有在有两个或三个存活邻居时继续存活. 尽管细胞数量可能无限, 但我们可以通过仅跟踪存活细胞来使用有限长度字符串编码状态. 如果我们在具有有限数量存活细胞的格局中初始化系统, 那么在所有未来步骤中存活细胞的数量将保持有限. 生命游戏的维基百科页面上有一些产生非常有趣演化的格局的美丽图形和动画.
由于生命游戏中的细胞排列在无限二维网格中, 它是二维元胞自动机的一个例子. 我们也可以考虑一维元胞自动机的更简单设置, 其中细胞排列在一条无限直线上, 参见图 8.10. 事实证明, 即使这个简单模型也足以实现图灵完备性. 我们现在将正式定义一维元胞自动机, 然后证明它们的图灵完备性.
有限格局: 如果自动机的格局中只有有限个索引在中使得 则我们称该格局是_有限的_. (即, 对于每个 有这样的格局可以使用一个有限字符串表示, 该字符串编码索引和值 由于 如果是有限格局, 则也是有限的. 我们只关心在有限格局中初始化的元胞自动机, 因此在其整个演化过程中保持有限格局.
8.4.1 一维元胞自动机的图灵完备性
我们可以编写一个程序(例如使用NAND-RAM)来模拟任何元胞自动机从初始有限格局的演化, 只需存储状态不等于的细胞值并重复应用规则 因此, 元胞自动机可以被图灵机模拟. 更令人惊讶的是, 反过来也成立. 例如, 尽管其规则简单, 我们可以使用生命游戏模拟图灵机(参见图 8.11).
图 8.11. 模拟图灵机的生命游戏格局. 图片由Paul Rendell提供
事实上, 即使一维元胞自动机也可以是图灵完备的:
为了使“模拟图灵机“的概念更精确, 我们需要定义图灵机的格局. 我们将在下面的8.4.2节中这样做, 但高层面上, 图灵机的格局是一个字符串, 编码了其在计算中给定步骤的完整状态. 即, 其磁带所有(非空)单元的内容、其当前状态以及磁头位置.
定理 8.2的证明的关键思想是, 在图灵机的计算中的每个点, 的磁带中唯一能改变的单元是磁头所在的位置, 并且该单元改变的值是其当前状态和的有限状态的函数. 这一观察使我们能够将图灵机的格局编码为一个元胞自动机的有限格局, 并确保此编码格局在的规则下的一步演化对应于图灵机执行中的一步.
8.4.2 图灵机格局与状态转移函数
为了将上述思想转化为定理 8.2的严格证明(甚至陈述! ), 我们需要精确定义图灵机的格局这一概念. 这个概念在后续章节中对我们也有用.
定义 8.3有一些技术细节, 但实际上并不深奥或复杂. 尝试花点时间停下来思考你如何将图灵机在执行中给定点的状态编码为一个字符串.
思考你需要知道哪些组件才能从此点继续执行, 以及使用有限符号列表编码它们的简单方法是什么. 特别是, 考虑到我们未来的应用, 尝试思考一种编码, 使得将步骤的格局映射到步骤的格局尽可能简单.
定义 8.3有点繁琐, 但无论怎么讲格局只是一个字符串, 编码了图灵机在执行中给定点的快照. (用操作系统术语, 它是一个“核心转储“(core dump))这样的快照需要编码以下组件:
- 当前磁头位置.
- 大容量存储器的完整内容, 即磁带.
- “本地寄存器“的内容, 即机器的状态.
我们如何编码格局的精确细节并不重要, 但我们确实想记录以下简单事实:
(为简化记号, 上面我们使用约定: 如果“越界”, 例如或 则我们假设我们将引理 8.1的证明留作练习8.7. 证明背后的思想很简单: 如果磁头既不在位置 也不在位置和 那么处的下一步格局将与之前相同. 否则, 我们可以从或其邻居的格局中“读取“图灵机的状态和磁头位置的磁带值, 并用其更新处的新状态应该是什么. 完成完整证明并不难, 但这样做是确保你熟悉格局定义的好方法.
完成定理 8.2的证明: 我们现在可以更正式地重述定理 8.2, 并完成其证明:
从定理 8.3的证明中产生的自动机具有大的字母表, 而且其大小依赖于被模拟的机器 事实证明, 人们可以获得一个具有固定大小字母表的自动机, 该字母表独立于被模拟的程序, 实际上自动机的字母表可以是最小集合! 图 8.13展示了这样的一个图灵完备的自动机.

图 8.13. 一维自动机的演化. 图中的每一行对应一个格局. 初始格局对应顶行, 仅包含一个“存活“细胞. 此图对应Stephen Wolfram的“规则110“自动机, 它是图灵完备的. 图片取自Wolfram MathWorld
我们可以使用与定义 8.3相同的方法来定义NAND-TM程序的格局. 这样的格局需要编码:
- 变量
i的当前值. - 对于每个标量变量
foo,foo的值. - 对于每个数组变量
Bar, 值Bar[]对于每个 其中是指标变量i在计算中曾达到的最大值.
8.5 λ演算与函数式编程语言
λ演算是定义可计算函数的另一种方式. 它有Alonzo Church在1930年代提出, 大约与Alan Turing提出图灵机同时. 有趣的是, 尽管图灵机不用于实际计算, λ演算却催生了函数式编程语言, 如Lisp、ML和Haskell, 并间接地促进了许多其他编程语言的发展. 在本节中, 我们将介绍λ演算并展示其能力等价于NAND-TM程序(因此也等价于图灵机). 我们的Github仓库包含一个Jupyter Notebook, 其中有一个λ演算的Python实现, 你可以通过实验来更好地理解这个话题.
λ算子: λ演算的核心是定义“匿名“函数的一种方式. 例如, 有一个函数的定义为
我们可以将其写为
因此 也就是说, 你可以将(其中是某个表达式)视为指定匿名函数的一种方式. 匿名函数使用、或其他密切相关的表示法, 出现在许多编程语言中. 例如, 在Python中我们可以使用lambda x: x*x来定义平方函数, 而在JavaScript中我们可以使用x => x*x或(x) => x*x. 在Scheme中我们会将其定义为(lambda (x) (* x x)). 显然, 函数的参数名称无关紧要, 因此与相同, 因为两者都对应平方函数.
省略括号: 为了减少表示上的杂乱, 在书写λ演算表达式时我们经常省略函数求值的括号. 因此, 与其将函数应用于输入的结果写为 我们也可以简单地写为 因此我们可以写 在本章中, 我们将同时使用和表示法进行函数应用. 函数求值是结合性的, 并从左到右绑定, 因此与相同.
8.5.1 函数的高阶应用
λ演算的一个核心特性是函数都是“一等公民“, 即我们可以将函数作为其他函数的参数. 比如说, 你能猜到下面这个表达式等于什么数字吗?
(8.1)可能看上去有点吓人, 但在你看下面的解答之前, 尝试将其分解为各个组成部分, 并一次计算一个部分. 完成这个例题将极大地有助于理解λ演算
让我们一步一步地计算(8.1). 尽管允许匿名函数是λ演算的优势, 但添加名称对于理解复杂表达式非常有帮助. 因此, 我们令与
因此, (8.1)可以写作 在输入函数时, 输出函数 换而言之, 是函数 我们的函数是简单的 因此是将映射到的函数. 因此
8.5.2 通过柯里化实现多参数函数
在形如的λ表达式中, 表达式本身也可以包含λ运算符. 比如如下函数 将映射到函数
特别地, 若我们使用调用函数(8.3)得到某个函数 再以调用 便可获得值 可以看出, 对应于的单参数函数(8.3)亦可视为双参数函数 一般地, 我们可以使用λ表达式来模拟双参数函数的效果, 这一技巧被称为柯里化(Currying). 我们将使用作为的简写形式. 若 则对应于对进行求值后, 将所得函数作用于 从而获得将中出现处替换为 出现处替换为的结果. 根据结合律, 该结果等价于 有时我们也写作
图 8.14. 在“柯里化“转换中, 我们可以通过λ表达式实现双参数函数的效果: 当输入时, 该表达式会输出一个单参数函数 其中已被“硬编码“至函数内, 且满足 这一过程可通过电路图直观展示, 详见Chelsea Voss的网站.
8.5.3 λ演算的形式化描述
我们现在提供λ演算的形式描述. 我们从包含单个变量的“基本表达式“开始, 例如或 并构建更复杂的表达式, 形为和 其中是表达式, 是变量标识符. 形式上, λ表达式的定义如下:
定义 8.4是一个递归定义, 因为我们在λ表达式的定义中使用了其自身. 这可能起初看起来令人困惑, 但事实上你从小学起就已经知道递归定义. 考虑我们如何定义算术表达式: 它是一个表达式, 要么只是一个数字, 要么具有形式 或 其中和是其他算术表达式.
自由变量和绑定变量: λ表达式中的变量可以是自由的(free)或绑定(bound)到一个运算符(在1.4.7节的意义上). 在单变量λ表达式中, 变量是自由的. 在应用表达式中, 自由和绑定变量的集合与底层表达式和的相同. 在抽象表达式中, 中的所有自由出现(free occurences)都被绑定到的运算符. 如果你觉得自由和绑定变量的概念令人困惑, 你可以通过为所有变量使用唯一标识符来避免所有这些问题.
优先级和括号: 我们将使用以下规则来允许我们省略一些括号. 函数应用从左向右结合, 因此与相同. 函数应用的优先级高于λ运算符, 因此与相同. 这类似于我们在算术运算中使用优先级规则来允许我们使用更少的括号, 比如表达式可以写成 如8.5.2节所述, 我们还使用简写表示 以及简写表示 这与使用λ表达式模拟多输入函数的“柯里化“转换很好地配合.
λ表达式的等价性: 正如我们在练习 8.1中看到的,规则等价于使我们能够修改λ表达式并获得更简单的等价形式. 另一个我们可以使用的规则是参数名称无关紧要, 因此与相同. 这些规则一起定义了λ表达式的等价性概念:
如果是一个形式为的λ表达式, 那么它自然对应于将任何输入映射到的函数. 因此, λ演算自然隐含了一个计算模型. 由于在λ演算中, 输入本身可以是函数, 我们需要决定以什么顺序求值一个表达式, 例如
对此有两种自然约定:
- 按名调用(Call-by-name, 即“惰性求值“): 我们通过先将右侧表达式作为输入代入左侧函数来求值(8.4), 得到然后从此继续.
- 按值调用(Call-by-value, 即“立即求值“): 我们先对右侧进行求值并得到 然后将其代入左侧得到来求值(8.4).
因为λ演算只有纯函数, 没有“副作用“, 所以在许多情况下顺序无关紧要. 事实上, 可以证明如果我们在两种策略中都得到一个确定的不可约表达式(irreducible expression)(例如, 一个数字), 那么它将是同一个. 然而, 为具体起见, 我们将始终使用“按名调用“(即惰性求值)顺序. (编程语言Haskell也做出了相同的选择, 尽管许多其他编程语言使用立即求值)形式上, 使用“按名调用“求值λ表达式的过程由以下过程描述:
对练习 8.2的解答
对练习 8.2的解答
的规范简化就是 为了计算的规范简化, 我们首先使用归约将代入中的 但由于在这个函数中根本未被使用, 我们简单地得到 它同样简化为
8.5.4 λ演算中的无限循环
与图灵机和NAND-TM程序类似, λ演算中的简化过程也可能进入无限循环. 例如, 考虑以下λ表达式
若我们尝试通过将左侧函数作用于右侧函数来简化(8.5), 则会得到另一个(8.5)的副本, 因此该过程永不休止. 在某些情况下, 求值顺序会影响表达式是否可被简化, 具体参见习题8.9.
8.6 增强λ演算
我们现在将λ演算作为一种计算模型进行讨论. 我们将从描述一个“增强“版本的λ演算开始, 它包含一些“冗余特性“, 但更易于理解. 我们将首先展示增强λ演算在计算能力上如何等价于图灵机. 然后, 我们将展示如何将“增强λ演算“的所有特性实现为“纯“(即非增强)λ演算之上的“语法糖“. 因此, 纯λ演算在计算能力上等价于图灵机(因此也等价于RAM机器和其他所有图灵等价模型).
增强λ演算包括以下对象和操作:
- 布尔常量和IF函数: 存在λ表达式 和 满足以下条件: 对于每个λ表达式和 且 也就是说, 是一个函数, 接受三个参数 当时输出 当时输出
- 二元组: 存在一个λ表达式 我们将其视为配对函数. 对于每个λ表达式 是二元对 其中是其第一个成员, 是其第二个成员. 我们还有λ表达式和 分别提取二元组的第一个和第二个成员. 因此, 对于每个λ表达式 且 (在Lisp中, 和函数传统上称为
cons,car和cdr) - 列表和字符串: 存在λ表达式 对应空列表, 我们也用 表示. 使用和 我们可以构造列表. 思路是, 如果是一个元素列表, 形式为 那么对于每个λ表达式 我们可以使用表达式获得元素列表 例如, 对于任意三个λ表达式 以下对应三元素列表
λ表达式在上返回 在其他任何列表上返回 字符串就是由比特组成的列表.
- 列表操作: 增强λ演算还包含列表处理函数 和 给定列表和函数 将应用于列表的每个成员, 得到新列表 给定列表和输出为或的表达式 返回列表 包含所有输出的的元素. 函数对列表应用“组合“操作. 例如, 将返回列表中所有元素的和. 更一般地, 接受列表 操作(我们视其为接受两个参数)和λ表达式(我们视其为操作的“中性元“, 例如加法为 乘法为 输出通过以下方式定义:
关于三个列表操作操作的图示, 请参见图 8.16.
- 递归: 最后, 我们希望能够执行递归函数. 由于在λ演算中函数是匿名的, 我们不能编写形式为 的定义, 其中包含对的调用. 相反, 我们使用函数 它接受一个额外输入作为参数. 运算符将接受这样的函数作为输入, 并返回的“递归版本“, 其中所有对的调用都替换为对此函数的递归调用. 也就是说, 如果我们有一个函数 接受两个参数和 那么将是函数 接受一个参数 使得对于每个
对练习 8.3的解答
对练习 8.3的解答
的等于 除非 因此
对练习 8.4的解答
对练习 8.4的解答
8.6.1 增强λ演算中的函数计算
一个增强λ表达式是通过将上述对象与应用和抽象规则组合而得到的. 简化λ表达式的结果是一个与远表达式等价的表达式, 因此如果两个表达式具有相同的简化结果, 则它们是等价的.
8.6.2 增强λ演算的图灵完备性
增强λ演算的基本操作或多或少相当于Lisp或Scheme编程语言. 鉴于这一点, 增强λ演算与图灵机等效或许并不令人惊讶:
定理 8.4的证明思路
定理 8.4的证明思路
为了证明该定理,我们需要证明 (1): 如果可由λ表达式计算, 则它可由图灵机计算, 以及 (2): 如果可由图灵机计算,则它可由增强λ表达式计算.
证明 (1) 相当直接.将简化规则应用于λ表达式基本上相当于“搜索和替换“,我们可以轻松地在NAND-RAM或Python中实现(两者在能力上都等价于图灵机). 证明 (2) 本质上相当于在函数式编程语言(如LISP或Scheme)中模拟图灵机(或编写NAND-TM解释器). 我们在下面给出细节, 但如何做到这一点是掌握一些本身就有用的函数式编程技术的良好练习.
定理 8.4的证明
定理 8.4的证明
我们仅给出证明的一个概述. “if“方向是简单的. 如上所述, 对λ表达式进行求值基本上相当于“搜索和替换”. 在命令式语言(如Python或C)中实现所有上述基本操作也是一个相当直接的编程练习, 并且使用相同的想法, 我们也可以在NAND-RAM中实现, 然后我们可以将其转换为NAND-TM程序.
对于“only if“方向,我们需要使用λ表达式模拟图灵机. 我们将通过首先为每个图灵机展示一个λ表达式来计算状态转移函数来实现这一点,该函数将的一个格局映射到下一个格局(见第8.4.2节).
的一个格局是一个字符串 其中是一个有限集合. 我们可以用有限字符串对每个符号进行编码, 因此我们将在λ演算中将格局编码为一个列表 其中是一个长度为的字符串(即一个由和组成的长度为的列表), 编码中的一个符号.
根据引理 8.1, 对于每个 等于 其中是某个有限函数. 使用我们对的编码 我们也可以将视为映射 到 通过练习 8.3,我们可以计算函数, 因此使用λ演算可以计算每个有限函数, 包括 利用这一见解, 我们可以使用λ演算计算如下. 给定一个编码格局的列表 我们定义列表和 分别编码格局向右和向左移动一步后的版本. 下一个格局定义为 其中表示的第个元素. 这可以通过递归(使用增强λ演算的运算符)计算如下:
一旦我们可以计算 我们就可以使用以下递归模拟在输入上的执行. 定义为从格局初始化时的最终格局. 函数可以递归定义如下:
检查一个格局是否停机(即, 转移函数是否输出可以轻松在λ演算中实现, 因此我们可以使用来计算 如果我们让是在输入上的初始格局, 那么我们可以从得到输出 从而完成证明.
8.7 从增强λ演算到纯λ演算
虽然我们所允许的增强型λ演算的“基本“函数集合比大多数Lisp方言提供的要小, 但从NAND-TM的角度来看, 它仍然显得有些“臃肿“. 我们能否用更少的函数来完成工作? 换句话说, 我们能否找到这些基本操作的一个子集, 使得该子集能够实现其余的操作?
事实上, 增强型λ演算的操作集合确实存在一个真子集, 可以用来实现其余所有操作. 这个子集就是空集.也就是说, 我们甚至可以不用和 仅使用λ运算符就能实现上述所有操作. 这完全是λ的天下!
这是一个很好的时机, 可以暂停一下, 思考你自己会如何实现这些操作. 例如, 可以先思考如何用来实现 然后如何结合与来实现 你也可以基于来实现 和 最具挑战性的部分是仅使用纯λ演算的操作来实现
定理 8.5背后的思想是, 我们将和本身编码为λ表达式, 并以此为基础进行构建. 这被称为Church编码(Church encoding), 因为它源于邱奇为了证明λ演算可以作为所有计算的基础所做的努力. 我们不会写出定理 8.5的完整形式化证明, 但会概述其中涉及的思想:
- 我们将定义为接受两个输入并输出的函数, 将定义为接受两个输入并输出的函数. 我们使用柯里化来实现双参数函数的效果, 因此且 (这种表示方案是表示
false和true的常见惯例, 但也有很多其他同样可行的表示和的替代方案) - 上述实现使得函数的实现变得平凡: 就是 因为且 我们可以写成以达到 的效果.
- 为了编码一个二元组 我们将产生一个函数 该函数在其“内部“包含和 并且对于每个函数都满足 也就是说, 我们可以通过写来提取二元组的第一个元素, 通过写来提取第二个元素, 因此且
- 我们将定义为忽略其输入并始终输出的函数. 即 函数在给定输入时, 检查如果我们将应用于函数(该函数忽略其两个输入并始终输出时是否得到 对于每个形式为 的有效二元组, 而 形式化地,
8.7.1 列表处理
现在我们面临一个更大的障碍, 即如何在纯λ演算中实现 和 事实证明, 我们可以用构建和 用构建 例如, 等同于 其中是对输入和输出的操作. (我将其验证留给读者你作为一个(推荐的)练习)
我们可以递归地定义 通过令 并规定给定一个非空列表(我们可以将其视为一个二元组 因此, 我们可能会尝试为编写一个递归的λ表达式, 如下所示:
这里唯一的问题是λ演算没有递归的概念, 因此这是一个无效的定义. 但当然, 我们可以使用我们的运算符来解决这个问题. 我们将把对““的递归调用替换为对作为额外参数给定的函数的调用, 然后将应用于此. 因此 其中:
8.7.2 Y组合子: 不需要递归的递归
(8.9)表明为了实现 与我们需要在纯λ演算中实现运算符. 这就是我们现在要做的事情.
我们如何在不使用递归的情况下实现递归?我们将用一个简单的例子来说明这一点 - 函数. 如练习 8.4所示, 我们可以递归地写出列表的函数如下:
其中是两个比特上的异或操作. 在Python中, 我们会这样写:
def xor2(a,b): return 1-b if a else b
def head(L): return L[0]
def tail(L): return L[1:]
def xor(L): return xor2(head(L),xor(tail(L))) if L else 0
print(xor([0,1,1,0,0,1]))
# 1
现在, 我们如何消除这个递归调用? 主要思想是, 既然函数可以接受其他函数作为输入, 那么在Python(当然还有λ演算)中, 给函数自身作为输入是完全合法的. 因此, 我们的想法是尝试提出一个非递归函数tempxor, 它接受两个输入: 一个函数和一个列表, 并且使得tempxor(tempxor,L)会输出L的异或值!
我们的第一次尝试可能只是简单地用me替换递归调用. 让我们将这个函数定义为myxor
def myxor(me,L): return xor2(head(L),me(tail(L))) if L else 0
让我们测试一下:
myxor(myxor,[1,0,1])
如果你这样做,解释器会给出以下错误:
TypeError: myxor() missing 1 required positional argument
问题是myxor期望两个输入: 一个函数和一个列表. 而在调用me时, 我们只提供了一个列表. 为了纠正这一点, 我们修改调用, 同时提供函数本身:
def tempxor(me,L): return xor2(head(L),me(me,tail(L))) if L else 0
注意在tempxor的定义中对me(me,..)的调用: 给定一个函数me作为输入, tempxor实际上会以自身作为第一个输入来调用函数me. 如果我们现在测试一下, 会发现实际上得到了正确的结果!
tempxor(tempxor,[1,0,1])
# 0
tempxor(tempxor,[1,0,1,1])
# 1
因此, 我们可以将xor(L)简单地定义为return tempxor(tempxor,L).
上述方法不仅适用于XOR. 给定一个接受输入x的递归函数f, 我们可以获得一个非递归版本, 如下所示:
- 创建函数
myf, 它接受两个输入me和x,并将对f的递归调用替换为对me的调用. - 创建函数
tempf,它将myf中形式为me(x)的调用转换为形式为me(me,x)的调用. - 函数
f(x)将被定义为tempf(tempf,x).
以下是我们如何在Python中实现RECURSE运算符的方式. 它将接受一个如上所述的函数myf, 并将其替换为一个函数g, 使得对于每个x, g(x)=myf(g,x).
def RECURSE(myf):
def tempf(me,x): return myf(lambda y: me(me,y),x)
return lambda x: tempf(tempf,x)
xor = RECURSE(myxor)
print(xor([0,1,1,0,0,1]))
# 1
print(xor([1,1,0,0,1,1,1,1]))
# 0
从Python到λ演算: 在λ演算中, 一个接受两个输入的函数被写作 因此, 函数被简单地写作 类似地, 函数就是 (你明白为什么吗?) 因此, 上述定义的函数tempf可以写作λ me. myf(me me). 这意味着, 如果我们将RECURSE的输入记为 那么 其中 或者换句话说
在线附录包含一个使用Python实现的λ演算. 以下是该附录中递归XOR函数的实现: 3
# XOR of two bits
XOR2 = λ(a,b)(IF(a,IF(b,_0,_1),b))
# Recursive XOR with recursive calls replaced by m parameter
myXOR = λ(m,l)(IF(ISEMPTY(l),_0,XOR2(HEAD(l),m(TAIL(l)))))
# Recurse operator (aka Y combinator)
RECURSE = λf((λm(f(m*m)))(λm(f(m*m))))
# XOR function
XOR = RECURSE(myXOR)
#TESTING:
XOR(PAIR(_1,NIL)) # List [1]
# equals 1
XOR(PAIR(_1,PAIR(_0,PAIR(_1,NIL)))) # List [1,0,1]
# equals 0
上述运算符更广为人知的名字是Y组合子(Y combinator).
它是一族不动点算子(fixed point operators)中的一个, 给定一个λ表达式 找到的一个不动点(fixed point) 使得 如果你思考一下就会发现, 就是上述的不动点. 是这样的函数: 对于每个 如果将作为的第一个参数代入, 我们会得到 换句话说 因此, 为找到不动点等同于对其应用
8.8 Church-Turing论题(讨论)
[1934年], 丘奇一直在思索, 并最终明确提出了λ可定义函数就是所有能行可计算函数的观点….当丘奇提出这一论点时, 我坐下来试图反驳它….但很快意识到[我的方法失败了], 一夜之间我成了该论点的支持者.
——斯蒂芬·克林,1979年.
我们定义了一个函数是可计算的, 如果它可以通过NAND-TM程序进行计算, 并且我们已经看到, 如果我们将NAND-TM程序替换为Python程序, 图灵机, λ演算, 元胞自动机以及许多其他计算模型, 该定义将保持不变. Church-Turing论题指出, 这是“可计算“函数的唯一合理定义. 与我们之前看到的“物理扩展Church-Turing论题“(PECTT)不同, Church-Turing论题并未做出可以通过实验检验的具体物理预测, 但它确实激励了诸如PECTT之类的预测. 我们可以将Church-Turing论题视为一种定义选择的提倡, 对所有潜在计算设备做出某种预测, 或者提出一些约束自然界的自然法则. 用Scott Aaronson的话来说, “无论它是什么, Church-Turing论题只能被视为极其成功”. 迄今为止, 尚无候选计算设备(包括量子计算机, 以及更不合理的模型, 例如我们之前提到的假设性“封闭时间曲线“计算机)对Church-Turing论题构成严肃挑战. 这些设备可能使某些计算更高效, 但并未改变有限可计算与不可计算之间的界限.(我们在第13.3节讨论的扩展Church-Turing论题规定, 图灵机也捕获了可高效计算内容的极限. 正如其物理版本所言, 量子计算对这一论题构成了主要挑战)
8.8.1 不同的计算模型
我们可以将我们已经看到的模型总结在以下表格中:
| 计算问题 | 模型类型 | 示例 |
|---|---|---|
| 有限函数 | 非均匀计算 (算法依赖于输入长度) | 布尔电路, NAND电路, 直线程序 (例如, NAND-CIRC) |
| 具有无界输入的函数 | 顺序访问内存 | 图灵机, NAND-TM程序 |
| – | 索引访问 / RAM | RAM机, NAND-RAM, 现代编程语言 |
| – | 其他 | λ演算, 细胞自动机 |
用于计算有限函数和任意输入长度函数的不同模型.
在第17章中, 我们将研究_内存受限_计算. 事实证明, 具有常量内存的NAND-TM程序等价于有限自动机(finite automata)模型(有时也会加上“确定性“或“非确定性“的形容词, 该模型也被称为有限状态机(finite state machines)), 它又捕获了正则语言(regular language)的概念(那些可以用正则表达式描述的语言), 这是我们将在第10章中看到的概念.
- 虽然我们使用图灵机定义了可计算函数, 但我们同样可以使用许多其他模型来定义, 不仅包括NAND-TM程序, 还包括RAM机, NAND-RAM, λ演算, 细胞自动机和许多其他模型.
- 非常简单的模型也可以是“图灵完备“的, 即它们可以模拟任意复杂的计算.
8.9 习题
令为以下函数. 输入是一个二元组 其中 是一个由键值对组成的列表的编码, 其中是二进制字符串. 输出是满足的最小对应的(如果这样的存在), 否则输出空字符串.
- 证明可由图灵机计算.
- 令为一个函数, 其输入是一个对组成的列表 其输出是通过将对添加到的开头而得到的列表 证明可由图灵机计算.
- 假设我们用一个键/值对的列表来编码一个NAND-RAM程序的配置, 其中键要么是标量变量名
foo, 要么是形如Bar[<num>]的形式(其中<num>是某个数字), 并且它包含所有非零的变量值. 令为一个函数, 它将NAND-RAM程序在某一时刻的配置映射到下一时刻的配置. 证明可由图灵机计算(你不需要实现每一个算术操作: 实现加法和乘法就足够了). - 证明对于每个可由NAND-RAM程序计算的函数 也可由图灵机计算.
令为一个函数, 其在输入一个编码三元组的字符串时, 如果和在中不连通, 则输出一个编码的字符串; 否则输出一个编码从到的最短路径长度的字符串. 证明可由图灵机计算. 参见脚注中的提示. 4
令为一个函数, 其在输入一个编码三元组的字符串时, 如果和在中不连通, 则输出一个编码的字符串; 否则输出一个编码从到的最长简单路径长度的字符串. 证明可由图灵机计算. 参见脚注中的提示. 5
证明对于每个不含自由变量的λ表达式 存在一个等价的λ表达式 该表达式仅使用变量 和 6
- 令 证明如果我们使用按名调用求值顺序, 则的简化过程会在确定的步数内结束; 而如果我们使用按值调用顺序, 则它永远不会结束.
- (加分, 挑战性)令为任意λ表达式. 证明如果使用按值调用顺序时简化过程会在确定的步数内结束, 那么使用按名调用顺序时它也会在确定的步数内结束. 参见脚注中的提示. 7
给出一个增强的λ演算表达式来计算函数 该函数在输入一对相同长度的列表和时, 输出一个由个对组成的列表 使得的第个元素(我们记为是对 因此将这两个元素列表“压缩“成一个由对组成的单个列表. 8
习题 8.12 (λ演算到NAND-TM编译器(挑战性)).
用你选择的编程语言给出一个程序, 该程序将λ表达式作为输入, 并输出一个NAND-TM程序 该程序计算与相同的函数. 为了部分得分, 你可以在输出程序中使用GOTO和所有NAND-CIRC语法糖. 你可以使用任何对你方便的λ表达式到二进制字符串的编码. 参见脚注中的提示. 10
这个问题将帮助你更好地理解图灵机状态转移函数的局部性概念. 这种局部性在诸如λ演算和一维元胞自动机的图灵完备性等结果中起着重要作用, 也出现在我们将在本课程后面看到的Godel不完备定理和Cook Levin定理等结果中. 定义STRINGS为具有以下语义的编程语言:
- 一个
STRINGS程序有一个单一的字符串变量str, 它既是的输入也是输出. 该程序没有循环也没有其他变量, 而是由一系列修改str的条件搜索和替换操作组成. STRINGS程序的操作包括:REPLACE(pattern1,pattern2), 其中pattern1和pattern2是固定字符串. 这将str中第一次出现的pattern1替换为pattern2.if search(pattern) { code }: 如果pattern是str的子串, 则执行code. 代码code本身可以包含嵌套的if语句. (也可以添加else { ... }来在pattern不是str的子串时执行).- 返回值是
str.
- 一个
STRINGS程序计算一个函数 如果对于每个 我们将str初始化为然后执行中的指令序列, 则在执行结束时str等于
例如, 以下是一个STRINGS程序, 它计算函数 使得对于每个 如果包含一个形如的子串, 其中 则 其中是通过将中第一次出现的替换为得到的.
if search('110011') {
replace('110011','00')
} else if search('110111') {
replace('110111','00')
} else if search('111011') {
replace('111011','00')
} else if search('111111') {
replace('1111111','00')
}
证明对于每个图灵机程序 存在一个STRINGS程序 它计算函数, 该函数将每个编码的有效配置的字符串映射到编码计算下一步的配置的字符串. (我们不关心该函数在那些不编码有效配置的字符串上的行为)你不必完整地写出STRINGS程序, 但你需要给出一个令人信服的论证, 证明这样的程序存在.
8.10 参考文献
Moore和Mertens的杰出著作(Moore, Mertens, 2011)第七章对这部分内容进行了精彩阐述.
RAM模型在研究实用算法的具体复杂度时非常有效, 其理论研究始于Cook和Reckhow(Cook, Reckhow, 1973). 不过需要注意的是, 不同文献和场景中对RAM模型允许的操作集及其成本定义存在差异. 正如Shamir(Shamir, 1979)已指出的, 在定义时需要特别谨慎——尤其是在字长可变的情况下. Savage著作(Savage, 1998)第三章给出了RAM机更形式化的描述, 亦可参阅Hagerup的论文(Hagerup, 1998). 关于不依赖输入规模的RAM算法研究(即transdichotomous RAM model)则由Fredman和Willard(Fredman, Willard, 1993)开创.
目前讨论的计算模型本质上是串行的, 但当今大量计算已转向并行模式——无论是通过多核处理器, 还是通过数据中心或互联网的大规模分布式计算. 虽然并行计算在实践中至关重要, 但对于“可计算与不可计算“的界限问题并未产生本质影响. 毕竟, 若计算任务可由台机器在时间内完成, 那么单台机器只需时间同样可以完成.
λ演算由Church(Church, 1941)提出. Pierce的专著(Pierce, 2002)是该领域权威教材, 另可参考Barendregt的著作(Barendregt, 1984). “柯里化“以逻辑学家Haskell Curry命名(Haskell编程语言同样得名于他). Curry本人认为这一概念应归功于Moses Schönfinkel, 但出于某种原因, “Schönfinkeling“这一术语始终未能流行.
与大多数编程语言不同, 纯λ演算不包含类型概念. 其中的每个对象既可视为λ表达式, 也可作为接收单参数并返回单值的函数. 所有函数均采用“搜索替换“机制:当传入非常规参数时, 系统会将形参全部替换为输入表达式的副本. λ演算的类型化变种已成为研究热点, 与编程语言类型系统及计算机可验证证明系统紧密关联(参见Pierce, 2002). 部分类型化λ演算变种摒弃了无限循环特性, 这使其成为程序静态分析和机器验证证明的重要工具, 我们将在第10章和第22章重新探讨这一主题.
陶哲轩曾提出通过证明流体动力学(“水计算机”)的图灵完备性来解决Navier-Stokes方程行为问题, 相关科普论述可参阅此文.
1: 一些编程语言可以访问的内存量有固定的(即使非常大)上限, 这正式地阻止了它们适用于计算无限函数并因此模拟图灵机. 我们在本次讨论中忽略此类问题, 并假定可以访问某种容量没有固定上限的存储设备.
2: 译者注: 在本翻译版中会使用中文
3: 由于Python语法的特定问题, 在此实现中, 我们使用f * g表示将f应用于g,而不是f g, 并使用λx(exp)而不是λx.exp进行抽象. 我们还使用_0和_1表示和的λ项, 以免与Python常量混淆.
4: 你不需要给出图灵机的完整描述:使用我们的“鱼与熊掌兼得“范式, 通过论证更强大的等价模型来证明这种机器的存在.
5: 与习题 8.4相同的提示. 注意, 为了证明是可计算的, 你不必给出一个高效的算法.
6: 提示: 你可以通过“将它们配对“来减少函数所使用的变量数量. 也就是说, 定义一个λ表达式 使得对于每个 是某个函数 满足且 然后使用迭代地减少所使用的变量数量.
7: 对表达式的结构使用归纳法.
8: 是这个操作的常用名称, 例如在Python中. 不要将其与zip压缩文件格式混淆.
9: 使用和(以及可能的 你可能还会发现习题 8.10中的函数有用.
10: 尝试建立这样一个过程: 如果数组Left包含λ表达式的编码, 并且数组Right包含另一个λ表达式的编码, 那么数组Result将包含
通用性和不可计算性
学习目标
- 通用机器/程序: “以一驭万“的单一程序
- 计算机科学与数学的基础结论: 不可计算函数的存在性
- 停机问题: 不可计算函数的典型范例
- 了解归约(reduction)这一技巧
- RIce定理: 不可计算性研究的“元工具“, 亦是编译器, 编程语言与软件验证领域众多研究的起点
“变量函数是由该变量与数字或常量以任意方式组合而成的解析表达式. “
——Leonhard Euler, 1748年
“通用机器的重要性显而易见. 我们无需制造无数台执行不同任务的机器……生产各类专用机器的工程问题, 已被为通用机器’编程’这类文书工作所取代. “
——Alan Turing, 1948年
我们在布尔电路(或等价的直线程序)研究中取得的最重要成果之一即是通用性(universality)这一概念: 存在可运行所有其他电路的单一电路. 然而该结论存在重要限制:运行包含个门电路的电路时, 通用电路所需门电路数量必须大于 事实证明, 图灵机或NAND-TM程序等均匀计算模型能帮助我们“突破此循环“, 并真正实现能运行所有其他机器的通用图灵机(universal turing machine) 其甚至能处理比自身更复杂(如具备更多状态)的机器. (同理, 存在能运行所有NAND-TM程序的通用NAND-TM程序(universialNAND-TMprogram) 包括那些比具有更多代码行的程序)
可以毫不夸张地说, 此类通用程序/机器的存在奠定了二十世纪后半叶(并持续至今)的信息技术革命根基. 在此之前的漫长历史中, 人类虽创造了诸如算盘, 计算尺及各类三角级数计算装置等专用计算设备, 但正如图灵(或许是最早洞见通用性的深远影响的思想家)所指出的, 通用计算机具有更强大的潜力. 当我们构建出能计算单一通用函数的设备后, 便获得了通过软件扩展其实现任意计算的能力. 例如要模拟新图灵机时, 无需重新构建实体机器, 只需将表示为字符串(即代码)并输入至通用机器即可.
除实际应用外, 通用算法的存在更具深远的理论意义, 尤其可用于证明不可计算函数(uncomputable functions)的存在, 此举颠覆了自Euler至Hilbert等数学家数百年来形成的数学直觉. 本章将论证通用程序的存在性, 并阐释其对不可计算性研究的启示, 详见图 9.1.
本章将展现计算机科学中的两项重大成果:
- 通用图灵机的存在性: 可运行所有其他算法的单一算法
- 不可计算函数的存在性: 任何算法都无法计算的函数(包括著名的“停机问题“)
我们将通过归约(reductions)技巧论证函数计算的困难性. 归约是借助“假想“能力(假设某函数可被计算)来推导其他函数计算途径的方法. 该技术当然广泛运用于编程领域:我们常将某些任务作为“黑箱“子程序来构建其他任务的算法. 但本章将采用“逆否“视角: 不再通过归约证明前项任务的“简易性“, 而是用以揭示后项任务的“困难性“. 如果你觉得归约费解无需担忧, 这一概念需要时日与实践方能掌握.
9.1 通用性或自循环解释器
我们首先证明通用图灵机的存在性. 这是一个独立的图灵机 能够模拟任意图灵机在任意输入上的运行, 甚至包括那些状态数和字母表规模都超过本身的图灵机 特别地,甚至可以用来运行自身! 这种自指(self reference)概念将在本书中反复出现, 并且正如我们将要看到的, 它会引发计算领域中诸多反直觉的现象.
图 9.2. 通用图灵机是一个独立的图灵机 当输入任意图灵机(以字符串形式描述)及其输入时, 能够计算在上的输出. 与图5.6所示的通用电路不同, 机器可以比复杂得多(例如具有更多状态或磁带字母符号).
定理 9.1的证明思路
定理 9.1的证明思路
9.1.1 证明通用图灵机的存在性
为证明(甚至准确表述)定理 9.1, 我们需要确定一种将图灵机表示为字符串的编码方式. 一种可能的方案是利用图灵机与NAND-TM程序的等价性, 从而用对应NAND-TM程序源代码的ASCII编码来表示图灵机 但我们将采用更直接的编码方式.
利用此表示法, 我们可以严格证明定理 9.1.
定理 9.1的证明
定理 9.1的证明
此处仅概述证明的主要思路. 首先注意到我们可以轻松编写一个Python程序, 该程序根据图灵机的表示和输入 在上对进行求值. 以下是该程序的具体代码(若不熟悉或不感兴趣可跳过):
# constants
def EVAL(δ,x):
'''Evaluate TM given by transition table δ
on input x'''
Tape = ["▷"] + [a for a in x]
i = 0; s = 0 # i = head pos, s = state
while True:
s, Tape[i], d = δ[(s,Tape[i])]
if d == "H": break
if d == "L": i = max(i-1,0)
if d == "R": i += 1
if i>= len(Tape): Tape.append('Φ')
j = 1; Y = [] # produce output
while Tape[j] != 'Φ':
Y.append(Tape[j])
j += 1
return Y
在输入转移表时, 该程序将逐步模拟对应图灵机的运行过程, 始终维持数组Tape包含的磁带内容, 变量s包含当前状态的不变性.
上述内容并未完全证明定理, 因为我们需要展示计算的是图灵机而非Python程序. 通过足够努力, 我们可以将此Python代码逐行转换为图灵机. 但为证明定理, 我们无需实际完成这一转换, 而是可以运用“鱼与熊掌兼得”范式: 虽然需要运行图灵机, 但在编写解释器代码时允许使用更强大的模型(如NAND-RAM), 因为根据定理8.1, 其与图灵机在计算能力上等价.
将上述Python代码转换为NAND-RAM程序非常直接. 唯一的问题是NAND-RAM没有内置存储转移函数δ的字典数据结构. 但我们可以将形如的字典表示为简单的键值对列表. 通过扫描所有键值对直到找到形式, 即可计算 类似地, 通过扫描列表并修改或追加键值对, 即可更新字典.
9.1.2 通用性的影响(讨论)

图 9.3. a) “元循环求值器”的一个特别优雅的示例来自John McCarthy在1960年的论文, 他在定义Lisp编程语言时给出了一个可求值任意Lisp程序的Lisp函数(见上图). Lisp最初并非作为实用编程语言设计, 此示例旨在说明Lisp通用函数比通用图灵机更优雅. 但麦卡锡的研究生史蒂夫·罗素建议将其实现. 据麦卡锡后来回忆: “我对他说, 呵呵, 你把理论和实践搞混了, 这个eval函数是用来阅读而不是计算的. 但他坚持做了下去——他将我论文中的eval编译成IBM 704机器码, 修复了一个错误, 然后将其作为Lisp解释器发布, 这确实名副其实. ” b) 汤普逊的经典论文(Thompson, 1984)中的自复制C程序.
满足定理 9.1条件的图灵机不止一个, 但即使仅存在一个这样的机器, 对计算机科学的理论与实践都具有极其重要的意义. 定理 9.1的影响超越了图灵机这一特定模型. 由于每个图灵机都可以被NAND-TM程序模拟, 反之亦然, 定理 9.1直接表明存在通用NAND-TM程序使得对每个NAND-TM程序成立. 我们还可以“混合搭配”不同模型: 由于每个NAND-RAM程序可被图灵机模拟, 每个图灵机可被演算模拟, 定理 9.1表明存在表达式 使得对每个满足的NAND-RAM程序和输入 若将编码为表达式(使用演算将字符串编码为0和1的列表), 则会求值为的编码. 更一般地说, 对于图灵等价模型集合{图灵机, RAM机器, NAND-TM, NAND-RAM,演算, JavaScript, Python……}中的任意和 都存在中的程序/机器, 可计算每个程序/机器的映射关系
“通用程序”的思想当然不仅限于理论. 例如编程语言的编译器常被用于编译自身以及比编译器更复杂的程序(Fabrice Bellard的Obfuscated Tiny C编译器就是典型例子: 这个2048字节的C程序能编译C编程语言的一个大型子集, 尤其能编译自身). 这也与可打印自身源代码的程序相关(见图 9.3). 目前已知存在需要极少状态或字母符号的通用图灵机, 特别是存在一种(基于特定图灵机字符串表示方法的)通用图灵机, 其磁带字母表为且状态数少于25个(见第9.7节).
9.2 所有函数都可计算吗?
在定理4.6中, 我们看到NAND-CIRC程序可以计算每个有限函数 因此, 一个很自然的猜想是, NAND-TM程序(或者等价地说, 图灵机)能够计算每个无限函数 然而, 事实并非如此. 也就是说, 存在一个函数是不可计算的!
不可计算函数的存在是相当令人惊讶的. 我们对“函数“的直观概念(也是直到20世纪大多数数学家所持有的概念)是, 函数定义了某种从输入计算输出的隐式或显式方法. 因此, “不可计算函数“这个概念看起来似乎自相矛盾, 但下面的定理表明, 这样的函数确实存在:
定理 9.2的证明思路
定理 9.2的证明思路
定理 9.2的证明
定理 9.2的证明
证明过程如图 9.4所示. 我们首先定义以下函数
对于每个字符串 如果满足**(1)是某个图灵机的有效表示(根据上述表示方案), 并且(2)**当程序在输入上执行时它停机并产生一个输出, 那么我们将定义为此输出的第一个比特. 否则(即, 如果不是图灵机的有效表示, 或者机器在上永不停机), 我们定义 我们定义
我们声称不存在计算的图灵机. 确实, 假设为了推出矛盾, 存在一台机器计算 并令是表示机器的二进制字符串. 一方面, 根据我们的假设,计算 在输入上, 机器停机并输出 另一方面, 根据的定义, 由于是机器的表示, 从而产生矛盾.
9.3 停机问题
定理 9.2表明存在某个无法计算的函数. 但是, 这个函数是否等同于“森林中无人听闻其倒下的树“呢? 也就是说, 它或许是一个实际上没有人想要计算的函数. 事实证明, 确实存在一些自然的不可计算函数:
在着手证明定理 9.3之前, 我们注意到是一个非常自然, 人们会想要计算的函数. 例如, 可以将视为管理“应用商店“任务的一个特例. 也就是说, 给定某个应用程序的代码, 商店的守门员需要决定此代码是否足够安全以允许进入商店. 至少, 我们似乎应该验证该代码不会进入无限循环.
定理 9.3的证明思路
定理 9.3的证明思路
定理 9.3的证明
定理 9.3的证明
该证明将使用先前已建立的结果定理 9.2. 回顾定理 9.2表明以下函数是不可计算的:
其中表示由字符串描述的图灵机在输入上的输出(按照通常约定, 如果此计算不停机, 则
我们将证明的不可计算性意味着的不可计算性. 具体来说, 我们将为了引出矛盾而假设存在一个能够计算函数的图灵机 并利用它来得到一个计算函数的图灵机 (这被称为_归约_证明, 因为我们将计算的任务归约到了计算的任务. 根据逆否命题, 这意味着的不可计算性蕴含着的不可计算性)
确实, 假设是一个计算的图灵机. 算法 9.1描述了一个计算的图灵机 (我们使用图灵机的“高层次“描述, 援引“鱼与熊掌兼得“范式, 见核心思想10)
我们断言算法 9.1计算了函数 确实, 假设(因此 在这种情况下, 因此在我们假设的条件下, 值将等于 因此算法 9.1将设定 并输出正确的值
假设否则(因此 在这种情况下, 有两种可能性:
- 情况1:: 由描述的机器在输入上不停机(因此 在这种情况下, 由于我们假设计算 这意味着在输入上, 机器必须停机并输出值 这意味着算法 9.1将设定并输出
- 情况2:: 由描述的机器在输入上停机并输出某个(因此 在这种情况下, 由于 根据我们的假设, 算法 9.1将设定 从而输出
我们看到在所有情况下, 这与不可计算的事实相矛盾. 因此, 我们对我们最初关于计算的假设得出了矛盾.
9.3.1 停机问题真的困难吗? (讨论)
许多人在初次看到定理 9.3的证明时, 第一反应是不敢相信. 也就是说, 虽然大多数人都相信这个数学结论, 但从直觉上看, 停机问题似乎并不真的那么困难. 毕竟, 不可计算性仅仅意味着无法被图灵机计算.
但程序员们似乎总能通过非正式或正式地论证其程序会终止, 来解决问题. 虽然他们的程序是用C或Python编写的, 而不是图灵机, 但这并无区别: 我们可以轻松地在这个模型与任何其他编程语言之间进行转换.
尽管每个程序员都曾遇到过无限循环, 但真的没有办法解决停机问题吗? 有些人声称, 只要他们足够努力地思考, 就能够判断任何给定的具体程序是否会终止. 甚至有人认为, 人类普遍具有这种能力, 因此人类天生就拥有优于计算机或其他由图灵机建模的事物的智能. 1
我们目前最好的答案是, 确实没有办法解决 无论是使用Mac, 个人电脑, 量子计算机, 人类, 还是任何其他电子, 机械和生物设备的组合. 实际上, 这一断言正是Church-Turing论题的内容. 当然, 这并不意味着对于每一个可能的程序 判断是否进入无限循环都很困难. 有些程序甚至根本没有循环(因此显然会终止), 并且还有许多其他不那么平凡的程序示例, 我们可以证明它们永远不会进入无限循环(或者我们确信它们会进入这样的循环). 然而, 并不存在一种通用方法, 能够对任意程序判断它是否终止. 此外, 有一些非常简单的程序, 没有人知道它们是否会终止. 例如, 以下Python程序当且仅当哥德巴赫猜想为假时才会终止:
def isprime(p):
return all(p % i for i in range(2,p-1))
def Goldbach(n):
return any( (isprime(p) and isprime(n-p))
for p in range(2,n-1))
n = 4
while True:
if not Goldbach(n): break
n+= 2
鉴于哥德巴赫猜想自1742年提出以来一直未被解决, 人类是否拥有任何神奇的能力来判断这个(或其他类似程序)是否会终止, 尚不清楚.

图 9.5. SMBC对解决停机问题的看法.
9.3.2不可计算性的直接证明(可选)
事实证明, 我们可以结合定理 9.2和定理 9.3的证明思路, 给出后者的一个简短证明, 而不需要诉诸的不可计算性. 这个简短证明出现在1965年Christopher Strachey写给《计算机杂志》编辑的一封信中:
致《计算机杂志》编辑.
一个不可能的程序
先生:
程序员间流传的一个众所周知的民间传说认为, 不可能编写一个程序来检查任何其他程序, 并在所有情况下判断它运行时是会终止还是进入封闭循环. 我从未在出版物上见过此事的证明, 尽管Alan Turing曾给过我一个口头证明(1953年在前往国家物理实验室参加会议的火车车厢里), 但我不幸立刻忘记了细节. 这让我有一种不安的感觉, 认为证明一定很长或很复杂, 但实际上它如此简短和简单, 一般的读者可能也会感兴趣. 以下版本使用了CPL, 但并非本质性的.
假设T[R]是一个布尔函数, 它以没有形式或自由变量的例程(或程序)R作为参数, 并且对于所有R, 如果R运行时终止, 则T[R] = True; 如果R不终止, 则T[R] = False.
考虑如下定义的例程P:
rec routine P
§L: if T[P] go to L
Return §
如果T[P] = True, 例程P将进入循环, 只有T[P] = False时它才会终止. 在每种情况下,T[P]的值都恰好是错误的, 这个矛盾表明函数T不可能存在.
您诚挚的,
C. Strachey
丘吉尔学院, 剑桥
尝试停下来, 从上面的信中提取证明定理 9.3的论证.
由于CPL如今已不常见, 让我们复现这个证明. 思路如下: 为了推出矛盾, 假设存在一个程序T, 使得T(f,x)等于True当且仅当f在输入x上停机. (Strachey的信考虑的是的无输入变体, 但我们会看到, 这一区别并非本质上的)然后我们可以构造一个程序P和一个输入x, 使得T(P,x)给出错误的答案. 思路是, 在输入x上, 程序P将执行以下操作: 运行T(x,x), 如果答案是True, 则进入无限循环, 否则停机. 现在你可以看到T(P,P)会给出错误的答案: 如果P在以其自身代码作为输入时停机, 那么T(P,P)本应为True, 但P(P)将进入无限循环. 而如果P不停机, 那么T(P,P)本应为False, 但P(P)却会停机. 我们也可以用Python编写这段代码:
def CantSolveMe(T):
"""
接受一个声称能解决停机问题的函数T.
返回一个由代码和输入组成的二元组(P,x)使
T(P,x) ≠ HALT(x)
"""
def fool(x):
if T(x,x):
while True: pass
return "我停机了"
return (fool,fool)
例如, 考虑以下天真的Python程序T, 它猜测一个给定的函数如果其输入包含while或for就不会停机:
def T(f,x):
"""粗略的停机测试器——如果程序含包含循环, 则判定其不停机"""
import inspect
source = inspect.getsource(f)
if source.find("while"): return False
if source.find("for"): return False
return True
如果我们现在设置(f,x) = CantSolveMe(T), 那么T(f,x)=False, 但f(x)实际上却停机了. 这当然不是这个特定T独有的问题: 对于每个程序T, 如果我们运行(f,x) = CantSolveMe(T), 我们都会得到一个输入, 在该输入上T对给出了错误的答案.
9.4 归约
停机问题被证明是不可计算性的关键, 因为定理 9.3已被用来证明大量有趣函数的不可计算性. 我们将在本章和练习中看到几个这样的结果示例, 但还有更多此类结果(见图 9.6).
这类不可计算性结果背后的思路在概念上很简单, 但起初可能相当令人困惑. 如果我们知道是不可计算的, 并且我们想证明某个其他函数是不可计算的, 那么我们可以通过逆否论证(即反证法)来实现. 也就是说, 我们证明如果存在一个计算的图灵机, 那么就存在一个计算的图灵机. (实际上, 这正是我们证明本身不可计算的方式, 即从定理 9.2的函数的不可计算性推导出这一事实)
例如, 为了证明是不可计算的, 我们可以证明存在一个可计算函数 使得对于每对和 都有 存在这样一个函数意味着, 如果是可计算的, 那么也将是可计算的, 从而导致矛盾! 关于归约令人困惑的部分在于, 我们假设一些我们相信为假的东西(即有算法), 以推导出一些我们知道为假的东西(即有算法). Michael Sipser将这类结果描述为具有 “如果猪能吹口哨, 那么马就能飞” 的形式.
基于归约的证明有两个组成部分. 首先, 由于我们需要是可计算的, 我们应该描述计算它的算法. 计算的算法被称为归约, 因为变换将的输入修改为的输入, 从而将计算的任务归约为计算的任务. 基于归约的证明的第二个组成部分是对算法的分析: 即证明确实满足所需的性质.
基于归约的证明与其他反证法类似, 但它们涉及那些并不真正存在的假设性算法, 这往往使得归约相当令人困惑. 唯一的一点慰藉是, 归根结底, 归约的概念在数学上非常简单, 因此, 即使你每次都需要回到基本原理来记住归约的方向, 也并不是那么糟糕.
备注 9.3 (归约是算法). 归约是一个算法, 这意味着, 如备注0.3所讨论的, 一个归约有三个组成部分:
- 规范(做什么): 在从到的归约中, 规范是函数应满足对于每个图灵机和输入 一般来说, 要将函数归约到 归约应满足对于的每个输入
- 实现(怎么做): 算法的描述: 将输入转换为输出的精确指令.
- 分析(为什么): 证明算法符合规范的证明. 特别地, 在从到的归约中, 这是证明对于每个输入 算法的输出满足
9.4.1 示例: 零输入停机问题
这里有一个通过归约进行证明的具体例子. 我们定义函数如下: 给定任意字符串当且仅当描述了一个在给定字符串作为输入时会停机的图灵机. 先验地,似乎比完整的函数可能更容易计算, 因此我们或许可以希望它是可计算的. 然而, 下面的定理表明情况并非如此:
定理 9.4的证明
定理 9.4的证明
该证明通过从归约来完成, 参见图 9.7. 为了推出矛盾, 我们假设可由某个算法计算, 并利用这个假想的算法来构造一个计算的算法 从而得到与定理 9.3的矛盾. (如重要启示10中所讨论的, 遵循我们“鱼与熊掌兼得“的范式, 我们只使用通用名称“算法“, 而不关心是将它们建模为图灵机, NAND-TM程序, NAND-RAM等; 这没有区别, 因为所有这些模型都是彼此等价的)
由于这是我们第一次从停机问题出发进行归约证明, 我们将比往常更详细地阐述它. 这样的归约证明包括两个步骤:
- 归约描述: 我们将描述我们的算法的操作, 以及它如何对假想的算法进行“函数调用“.
- 归约分析: 然后我们将证明, 在算法计算的假设下, 算法将计算
我们的算法工作如下: 在输入上, 它运行算法 9.1以获得一个图灵机 然后返回 机器忽略其输入 只运行于上.
在伪代码中, 程序看起来大致如下:
def N(z):
M = r'.......' # 包含 M 描述的字符串常量
x = r'.......' # 包含 x 的字符串常量
return eval(M,x) # 注意我们忽略了输入 z
也就是说, 如果我们将视为一个程序, 那么它是一个包含和作为“硬编码常量“的程序, 给定任何输入 它 simply 忽略输入并总是返回在上运行的结果. 算法并不实际执行机器仅仅将的描述作为字符串写下(就像我们上面做的那样), 并将这个字符串作为输入提供给
以上完成了归约的描述. 分析通过证明以下断言获得:
断言: 对于每个字符串 由算法在步骤1中构造的机器满足:在上停机当且仅当由描述的程序在输入上停机.
断言证明: 由于忽略其输入并使用通用图灵机在上评估 它在上停机当且仅当在上停机.
特别地, 如果我们用输入来实例化这个断言, 我们看到 因此, 如果假想的算法对每个满足 那么我们构造的算法对每个满足 这与的不可计算性相矛盾.

图 9.8. 一个Python实现, 展示了如果不可计算, 则也不可计算的归约. 有关此归约的完整实现, 请参见此Colab笔记本.
在定理 9.4的证明中, 我们使用了将输入“硬编码“到程序/机器中的技术. 也就是说, 我们取一个计算函数的程序, 并将一些输入“固定“或“硬编码“为某个常数值. 例如, 如果你有一个程序, 它接受一对数字作为输入并输出它们的乘积(即计算函数 那么你可以将第二个输入“硬编码“为 从而获得一个程序, 它接受一个数字作为输入并输出(即计算函数 这种技术在归约证明和其他地方非常常见, 我们将在本书中反复使用它.
9.5 Rice定理与通用软件验证的不可能性
停机问题的不可计算性其实是一个更普遍现象的特殊情况. 即, 我们无法证明通用程序的语义属性. “语义属性“指的是程序计算的函数的属性, 而不是依赖于程序使用的特定语法的属性.
程序的语义属性的一个例子是: 只要被给定一个具有偶数个的输入字符串, 它就输出 另一个例子是: 当输入以结尾时,将始终停机. 相比之下, C程序在每个函数声明之前包含注释的属性不是语义属性, 因为它依赖于实际的源代码, 而不是输入/输出关系.
检查程序的语义属性非常重要, 因为它对应于检查程序是否符合规范. 但结果证明这样的属性通常是不可计算的. 我们已经看到了一些不可计算语义函数的例子, 即和 但这些只是“冰山一角“. 我们首先观察另一个这样的例子:
定理 9.5的证明
定理 9.5的证明
证明通过从归约来完成. 为了推出矛盾, 假设存在一个算法 使得对每个 那么我们将构造一个算法来解决 从而与定理 9.4矛盾.
给定一个图灵机(它是的输入), 我们的算法执行以下操作:
- 构造一个图灵机 它在输入上, 首先运行 然后输出
- 返回
现在, 如果在输入上停机, 那么图灵机计算常数零函数, 因此在我们假设计算的情况下, 如果在输入上不停机, 那么图灵机在任何输入上都不会停机, 因此特别地, 它不计算常数零函数. 因此在我们假设计算的情况下, 我们看到在两种情况下, 因此算法在步骤 2 返回的值等于 这正是我们需要证明的.
另一个类似的结果如下:
9.5.1 Rice定理
定理 9.6可以推广到远不止奇偶校验函数. 事实上, 这种推广排除了对程序进行任何类型的语义规约验证的可能性. 我们将程序上的一个语义规约(semantic specification)定义为某种不依赖于程序代码, 而只依赖于程序所计算的函数的性质.
例如, 考虑以下两个C程序:
int First(int n) {
if (n<0) return 0;
return 2*n;
}
int Second(int n) {
int i = 0;
int j = 0
if (n<0) return 0;
while (j<n) {
i = i + 2;
j = j + 1;
}
return i;
}
First和Second是两个不同的C程序, 但它们计算相同的函数. 一个语义性质, 对这两个程序要么同时为真, 要么同时为假, 因为它依赖于程序计算的函数, 而不是它们的代码. First和Second都满足的一个语义性质的例子是: “程序计算一个将整数映射到整数的函数 满足对于每个输入 ”.
如果一个性质依赖于源代码本身而不是输入/输出行为, 那么它就是非语义的. 例如, “程序包含变量k” 或 “程序使用了while操作” 等性质就不是语义的. 这样的性质可能对一个程序为真, 而对其他程序为假.
形式化地, 我们定义语义性质如下:
如果对于每个 都有 则称一对图灵机和是功能等价的(functionally equivalent). (特别地, 对于所有当且仅当
一个函数是语义的, 如果对于每一对表示功能等价图灵机的字符串 都有 (回想一下, 我们假设每个字符串都表示某个图灵机, 参见备注 9.1)
语义函数有两个平凡的例子: 常值1函数和常值0函数. 例如, 如果是常零函数(即, 对于每个 那么显然对于每一对功能等价的图灵机和 都有 下面是一个非平凡的例子:
对练习 9.1的解答
对练习 9.1的解答
回想一下,当且仅当对于每个 如果和功能等价, 那么对于每个 因此,当且仅当
通常, 我们最感兴趣计算的程序性质是语义的, 因为我们希望理解程序的功能. 不幸的是, Rice定理告诉我们这些性质都是不可计算的:
定理 9.7的证明思路
定理 9.7的证明思路
定理 9.7的证明
定理 9.7的证明
我们不会给出完全形式化的证明, 而是通过将注意力限制在一个特定的语义函数上来阐述证明思路. 然而, 同样的技术可以推广到所有可能的语义函数. 定义如下: 如果不存在和两个输入 使得对于每个 但输出且 也就是说,如果不可能找到一个输入 使得将的某些位从0翻转为1会将的输出从1反方向改变为0. 我们将证明是不可计算的, 但该证明很容易推广到任何语义函数.
我们首先注意到既不是常值零函数, 也不是常值一函数:
- 在所有输入上直接进入无限循环的机器满足 因为在任何地方都没有定义, 因此特别地, 不存在两个输入 使得对于每个有 但且
- 计算其输入的或奇偶性(异或)的机器不是单调的(例如,但 因此
(注意和是机器而不是函数)
现在, 我们将给出一个从到的归约. 也就是说, 我们假设存在一个计算的算法 并由此导出矛盾, 然后我们将构建一个计算的算法 我们的算法将如下工作:
- 算法
- 输入: 描述图灵机的字符串 (目标: 计算
- 假设: 可以访问计算的算法
- 操作:
- 构造以下机器 “对于输入 执行: (a) 运行 (b) 返回”.
- 返回
为了完成证明, 我们需要证明, 在我们假设计算的前提下,输出了正确答案. 换句话说, 我们需要证明 假设在输入 0 上不停机. 在这种情况下, 算法构造的程序在步骤 (a) 进入无限循环, 并且永远不会到达步骤 (b). 因此, 在这种情况下,功能等价于 (机器与不是同一个机器: 它的描述或代码不同. 但它的输入/输出行为(在这种情况下)确实相同, 即在任何输入上都不停机. 另外, 虽然程序将在每个输入上进入无限循环, 但算法从未实际运行 它只生成其代码并将其提供给 因此, 即使在这种情况下, 算法也不会进入无限循环)所以在这种情况下,
如果在输入0上确实停机, 那么中的步骤**(a)** 最终将结束, 并且的输出将由步骤**(b)** 决定, 即它简单地输出其输入的奇偶性. 因此, 在这种情况下,计算的是非单调的奇偶性函数(即功能等价于 所以我们得到 在这两种情况下, 这正是我们想要证明的.
检查这个证明可以发现, 除了是语义且非平凡的之外, 我们没有使用关于它的任何其他信息. 对于每个语义的非平凡函数 我们可以使用相同的证明, 只需将和替换为两个机器和 使得且 如果是非平凡的, 这样的机器必须存在.
Rice定理非常强大, 并且是证明不可计算性的一种流行方法, 以至于人们有时会感到困惑, 认为它是证明不可计算性的唯一方法. 特别地, 一个常见的误解是, 如果一个函数不是语义的, 那么它就是可计算的. 这完全不是事实.
例如, 考虑以下函数 这个函数在输入一个表示NAND-TM程序的字符串时, 输出当且仅当 (i)在输入上停机, 并且 (ii) 程序不包含标识符为Yale的变量. 函数显然不是语义的, 因为当输入以下两个功能等价程序之一时, 它将输出两个不同的值:
Yale[0] = NAND(X[0],X[0])
Y[0] = NAND(X[0],Yale[0])
Harvard[0] = NAND(X[0],X[0])
Y[0] = NAND(X[0],Harvard[0])
然而,是不可计算的, 因为每个程序都可以被转换成一个等价的(实际上是更好的:)) 程序 该程序不包含变量Yale. 因此, 如果我们能计算 那么我们就能判定NAND-TM程序(从而也能判定图灵机)在输入0上是否停机.
此外, 正如我们将在第11章中看到的, 存在一些不可计算函数, 其输入不是程序, 因此形容词“语义的“并不适用.
诸如“程序包含变量Yale“之类的性质有时被称为语法性质. “语义的“和“语法的“这两个术语的使用超出了编程语言的范围: 英语中一个著名的语法正确但语义无意义的句子是乔姆斯基的“Colorless green ideas sleep furiously.”(无色的绿色思想愤怒地睡觉)然而, 形式化定义“语法性质“相当微妙, 本书将不使用这个术语, 只使用“语义的“和“非语义的“这两个术语.
9.5.2 其他图灵完备模型的停机问题与Rice定理
正如我们之前所见, 许多自然计算模型被证明是彼此等价的, 因为我们可以将一个模型的“程序“(例如表达式, 或生命游戏的格局)转换成另一个模型(例如NAND-TM程序). 这种等价性意味着, 我们可以将NAND-TM程序的停机问题的不可计算性转化为其他模型中停机问题的不可计算性. 例如:
定理 9.8的证明
定理 9.8的证明
同样的证明也适用于其他计算模型, 如 演算, 二维(甚至一维)自动机等. 因此, 例如, 没有算法可以判定一个表达式是否计算恒等函数, 也没有算法可以判定生命游戏的初始格局最终是否会将单元格染成黑色.
事实上, 我们可以将Rice定理推广到所有这些模型. 例如, 如果是一个非平凡函数, 使得对于每对功能等价的NAND-TM程序都有 那么是不可计算的, 这对于NAND-RAM程序, 表达式以及所有其他图灵完备模型(如定义8.5所定义)同样成立, 另见习题 9.12.
9.5.3 软件验证被摧毁了吗? (讨论)
程序正越来越多地用于关键任务, 无论是运行我们的银行系统, 驾驶飞机还是监控核反应堆. 如果我们甚至无法提供一个认证算法来证明一个程序正确计算了奇偶校验函数, 那么我们怎么能确信一个程序做了它应该做的事情呢?关键见解是, 虽然不可能认证一个通用程序符合规约, 但可以在最初编写程序时采用一种使其更容易认证的方式. 举个简单的例子, 如果你编写一个没有循环的程序, 那么你可以证明它会停机. 此外, 虽然可能无法认证一个任意程序计算了奇偶校验函数, 但完全可以编写一个特定的程序 我们可以从数学上证明计算了奇偶校验. 事实上, 编写程序或算法并提供其正确性证明, 正是我们在算法研究中一直在做的事情.
软件验证(software verification)领域关注的是验证给定程序是否满足某些条件. 这些条件可以是程序计算了某个函数, 永远不会写入危险的内存位置, 遵守某些不变量等等. 虽然验证这些任务的一般性问题可能是不可计算的, 但研究人员已经成功地对许多有趣的案例进行了验证, 特别是如果程序最初就是用一种使验证更容易的形式化方法或编程语言编写的. 尽管如此, 验证, 尤其是大型复杂程序的验证, 在实践中仍然是一项极具挑战性的任务, 并且已被形式化证明正确的程序数量仍然很少. 此外, 即使是提出要证明的正确定理(即规约)本身, 也常常是一项非常重要的任务.
图 9.9. 可计算布尔函数集合(定义7.3)是所有将映射到的函数集合的真子集. 在本章中, 我们看到了后者集合中一些不在前者集合中的元素的例子.
- 存在一个通用图灵机(或NAND-TM程序) 使得在输入图灵机的描述和某个输入时,停机并输出 当(且仅当)在输入上停机. 与有限计算(即NAND-CIRC程序/电路)的情况不同, 程序的输入可以是一个状态数比本身更多的机器
- 与有限情况不同, 实际上存在一些本质上不可计算的函数, 即它们不能被任何图灵机计算.
- 这些不仅包括一些“退化“或“深奥“的函数, 还包括人们深切关注并曾猜想可以计算的函数.
- 如果Church-Turing论题成立, 那么根据我们的定义不可计算的函数 在我们的物理世界中无法通过任何方式计算.
9.6 习题
设函数满足: 对于输入(表示三元组的)字符串, 当且仅当图灵机在输入上, 在其读写头到达其纸带的第个位置之前停机. (我们不关心执行了多少步, 只要读写头始终保持在位置内即可)证明是可计算的. 提示见脚注2
证明下列函数是不可计算的. 对于输入 我们定义当且仅当是一个表示NAND++程序的字符串, 并且只有有限个输入满足 3
不使用Rice定理证明定理 9.6.
定义函数如下: 给定一个表示图灵机对的字符串, 当且仅当和根据定义 9.2是功能等价的. 证明是不可计算的.
注意, 你不能直接使用Rice定理, 因为该定理只处理以单个图灵机作为输入的函数, 而接收两个机器作为输入.
设为如下定义的函数. 对于输入一个表示NAND-RAM程序的字符串和一个表示图灵机的字符串 当且仅当存在某个输入使得在上停机而在上不停机. 证明是不可计算的. 提示见脚注. 4
习题 9.12 (适用于通用图灵等价模型的Rice定理(可选)).
设为所有从到的部分函数的集合, 是定义8.5中定义的图灵等价模型. 我们称一个函数是*-语义的*, 如果存在某个使得对于每个都有
证明对于每个既非常数也非常数的-语义函数 是不可计算的.
本题中我们定义忙碌海狸函数的NAND-TM变体(参见Aaronson于1999年的论文, 2017年的博客文章和2020年的综述(Aaronson, 2020); 另见Tao关于文明科学进步如何通过我们能理解的量来衡量的演讲).
- 定义如下: 对于每个字符串 如果表示一个NAND-TM程序, 并且当在输入上执行时在步内停机, 则 否则(如果不代表一个NAND-TM程序, 或者它是一个在上不停机的程序), 证明是不可计算的.
- 令表示数(即高度为的“二的幂塔”). 为了体会这个函数增长有多快, 而大约是 已经是一个即使用科学记数法也难以书写的巨大数字. 定义(代表“NAND-TM Busy Beaver“)为函数 其中如问题6.1所定义. 证明的增长速度快于 即 提示见脚注9
5.9 参考书目
图 9.1中关于停机问题的漫画取自Charles Cooper的网站, 版权归2019年Charles F. Cooper所有.
(Moore与Mertens, 2011年)第7.2节对不可计算性作了高度推荐的概述. 《Gödel, Escher, Bach》(Hofstadter, 1999年)是一本经典科普著作, 涉及不可计算性, 不可证明性, 特别是我们将在第11章看到的哥德尔定理. 亦可参考Holt的新书(Holt, 2018年).
函数定义的历史与数学作为一个领域的发展交织在一起. 多年以来, 函数被(依照上述Euler的表述)视为从输入计算输出的方法. 19世纪, 随着Fourier级数的发明以及对连续性和可微性的系统研究, 人们开始关注更一般的函数类型, 但将函数定义为任意映射的现代定义尚未被普遍接受. 例如, Poincare在1899年写道:*“我们见到大量奇异的函数, 它们似乎被迫尽可能不像那些有实际用途的正当函数…这些函数被特意构造出来, 只为证明我们先辈的推理存在缺陷, 除此之外我们从中得不到任何东西”*部分精彩的历史论述可参阅(Grabiner, 1983)(Kleiner, 1991)(Lützen, 2002)(Grabiner, 2005).
通用图灵机的存在以及的不可计算性最早由Turing在其开创性论文(Turing, 1937)中证明, 但Church在前一年已证明了密切相关的结论. 这些工作建立在Gödel1931年的不完备性定理基础上, 我们将在第11章讨论该定理.
(Rogozhin, 1996)给出了一些字母表和状态数较小的通用图灵机, 包括采用二进制字母表且状态数少于的单带通用图灵机;亦可参阅综述(Woods与Neary, 2009). Adam Yedidia开发了辅助生成较少状态灵机的软件. 这与“代码高尔夫”这种娱乐活动相关, 旨在用尽可能短的程序解决特定计算任务. 寻找“高度复杂“的小型图灵机也与“忙碌海狸“问题有关, 参见习题 9.13及综述(Aaronson, 2020).
用于证明不可计算性的对角线论证法源于第2章讨论的康托尔关于实数不可数的论证.
Christopher Strachey是英国计算机科学家, CPL编程语言的发明者. 他也是早期人工智能领域的先驱, 在1950年代初期就编程使计算机能下跳棋甚至写情书, 详见《纽约客》文章与此网站.
Rice定理在(Rice, 1953)中被证明. 其常见表述形式与我们所采用的略有不同, 参见习题 9.11.
本章未讨论递归可枚举语言的概念, 但习题 9.10简要涉及了该内容. 我们照例使用函数记法而非语言记法.
1: 这一论点也与意识和自由意志的问题相关. 我个人对其与这些问题的相关性持怀疑态度. 或许推理过程是: 人类有能力解决停机问题, 但他们通过选择不这样做来行使自由意志和意识.
2: 一台字母表为的机器, 其纸带前个位置的内容最多有种可能. 如果机器重复了之前出现过的配置(即纸带内容, 读写头位置和当前状态都与之前某个执行状态完全相同), 会发生什么?
3: 提示: 你可以使用Rice定理.
4: 提示: 虽然不能直接应用, 但稍作“调整“后, 你可以使用Rice定理来证明这一点.
5: 具有此性质.
6: 你可以使用对角化方法直接证明, 或者证明所有递归可枚举函数的集合是可数的.
7: 具有此性质: 证明如果和都是递归可枚举的, 那么实际上将是可计算的.
8: 证明任何满足 (b) 的都必须是语义的.
9: 在本练习中, 你不需要使用函数非常具体的性质. 例如, 的增长也快于Ackerman函数.
❗页面施工中: 目前状态: 创建教程中.
要求:
- ✅将所有numthm环境用灰色admonish(quote)框起.
- ✅标点符号统一为英文.
- ✅使用添加对文内特定位置的超链接.
- ✅使用添加引用.
- ⬛️重要概念框.
量子计算
学习目标
- 了解量子力学与局部确定性理论的主要不同之处
- 量子电路模型,或等价的 QNAND-CIRC 程序
- 复杂度类 及其与其他复杂度类关系的现有知识
- Shor 算法和量子傅里叶变换背后的思想
“我们一直以来(这是秘密!关门再听!)……都很难理解量子力学所代表的世界观……对我来说,目前还没有明显的证据表明这里没有真正的问题……我能否通过提出一个问题——一个关于计算机、关于量子力学世界观(这种或许存在、或许不存在的谜团)的问题——学到些什么呢?”
—Richard Feynman,1981年
目录
古希腊有两大学派的自然哲学观点。 亚里士多德认为,万物具有解释其行为的“本质”,对自然世界的理论必须涉及事物表现出某些现象的根本原因(用亚里士多德的话说就是“final cause“)。 德谟克利特则主张对世界进行纯粹机械的解释。在他看来,宇宙最终由基本粒子(即“原子”)组成,我们所观察到的现象,源于这些粒子按照某些局部规则相互作用的结果。 现代科学(可以说从牛顿开始)基本上采纳了德谟克利特的观点,即认为世界是由粒子和作用于它们的力组成的机械的、精密的宇宙系统。
尽管粒子和力的分类随着时间推移有所演变,但从牛顿到爱因斯坦,整体的“宏观图景”并没有太大变化。 特别是,有一个被当作公理的观点:如果我们完全了解宇宙当前的“状态”(即粒子及其属性,如位置和速度),那么我们就可以在任何时刻预测它的未来状态。 用计算语言来说,在所有这些理论中,一个包含 个粒子的系统状态可以用 个数字的数组来存储,而预测系统的演化则可以通过对这个数组运行某种高效(例如 时间)的确定性计算来完成。
双缝实验
然而,到了20世纪初,一些实验结果开始对这种机械且精确的世界观提出质疑。(原文表述为 “clockwork” or “billiard ball” theory of world ——译者注)其中一个著名的实验就是双缝实验。 我们可以这样描述它:假设我们买了一台棒球发射机,对准一个软塑料墙发射棒球,但在发射机和塑料墙之间放置一个带有单个缝隙的金属屏障(见 doublebaseballfig{.ref})。 如果我们向塑料墙发射棒球,一些棒球会被金属屏障弹开,而另一些则会通过缝隙击中墙面并留下凹痕。 如果我们在金属屏障上再开一个缝隙,就会有更多的棒球通过,从而塑料墙上的凹痕会变得更多。